® OpenGIS Implementation Specification for Geographic information - Simple feature access - Part 1: Common architecture

Category: OpenGIS® Implementation Specification
Editor: John R. Herring

Перевод с английского: Григорива О.М.

Copyright © 2006 Open Geospatial Consortium,
Inc. All Rights Reserved. http://www.opengeospatial.org/legal/ To obtain additional rights of use, visit
Источник: сайт | спецификация

1. ТЕКСТОВОЕ ПРЕДСТАВЛЕНИЕ ГЕОМЕТРИИ (WKT)

1.1 Обзор

Каждый Тип Геометрии имеет свое представление в текстовом виде (далее - представление WKT), которое может быть использовано как для создания новых экземпляров объектов данного типа, так и для преобразования существующих экземпляров объектов в текстовый вид для буквенно-цифрового отображения.

1.2 Описание

1.2.1 Представление BNF

Представление WKT Геометрии определено ниже с использованием BNF.

  1. Обозначение "{}" указывает на необязательный элемент внутри скобок. Скобки в выходном списке элементов не отображаются.
  2. Обозначение "()" группирует последовательность элементов в один элемент. Также не отображается в выходном списке.
  3. Обозначение "*" после элемента указывает на возможное использование нескольких экземпляров данного элемента.
  4. Строка символов без специальных обозначений определяет строку как элемент.
  5. Обозначение "|" определяет выбор между двумя элементами и не отображается в выходном списке.
  6. Обозначение "< >" содержит производный тип либо основной тип, определенный где-либо в списке.
  7. Обозначение ":=" предполагает замену выражения слева от обозначения на выражение справа от обозначение. Операция прекращается, когда выражению слева приравнивается неопределенное ранее значение.

Текстовое представление геометрии должно базироваться на описанных принципах. Строка WKT (см. гл. 6) является нечувствительной к регистру. Поэтому, когда важна читабельность, может быть использован верхний регистр (т.е. написание служебных слов заглавными буквами, см. примеры в данной спецификации).

Примечание:
Все производные строки разделяются по координатному типу. Это значит, что любые два субэлемента любого элемента
будут иметь такой же координатный тип, что и родительский элемент.

Правила, описанные в этом и предыдущем разделах, позволяют компактно и читабельно описывать текстовые представления геометрии объектов. Представление геометрии объектов, состоящих из однородных компонентов, не содержит тэгов каждого дочернего компонента. Нижеследующий набор строк описывает представление чисел двойной точности в текстовом виде.

<x> ::= <signed numeric literal>
<y> ::= <signed numeric literal>
<z> ::= <signed numeric literal>
<m> ::= <signed numeric literal>
<quoted name> ::= <double quote> <name> <double quote>
<name> ::= <letters>
<letters> ::= (<letter>)*
<letter> ::= <simple Latin letter>||
<simple Latin letter> ::= <simple Latin upper case letter>
|<simple Latin lower case letter>
<signed numeric literal> ::= {<sign>}<unsigned numeric literal>
<unsigned numeric literal> ::= <exact numeric literal>
|<approximate numeric literal>
<approximate numeric literal> ::= <mantissa>E<exponent>
<mantissa> ::= <exact numeric literal>
<exponent> ::= <signed integer>
<exact numeric literal> ::= <unsigned integer>
{<decimal point>{<unsigned integer>}}
|<decimal point><unsigned integer>
<signed integer> ::= {<sign>}<unsigned integer>
(<digit>)*
<left delimiter> ::= <left paren>|<left bracket>
// должен быть выровнен по правому разделителю
<right delimiter> ::= <right paren>|<right bracket>
// должен быть выровнен по левому разделителю
<special> ::= <right paren>|<left paren>|<minus sign>
|<underscore>|<period>|<quote>|<space>
<sign> ::= <plus sign> | <minus sign>
<decimal point> ::= <period> | <comma>
<empty set> ::= EMPTY
<minus sign> ::= -
<left paren> ::= (
<right paren> ::= )
<left bracket> ::= [
<right bracket> ::= ]
<period> ::= .
<plus sign> ::= +
<double quote> ::= "
<quote> ::= '
<comma> ::= ,
<underscore> ::= _
<digit> ::= 0|1|2|3|4|5|6|7|8|9
<simple Latin lower case
letter> ::=		 a|b|c|d|e|f|g|h|i|j|k|l|m
|n|o|p|q|r|s|t|u|v|w|x|y|z
<simple Latin upper case
letter> ::= 		A|B|C|D|E|F|G|H|I|J|K|L|M
|N|O|P|Q|R|S|T|U|V|W|X|Y|
<space>= " "
// уникод "U+0020" (пробел)

1.2.2 BNF-описание для Двумерной WKT геометрии

Данный BNF определяет двумерную геометрию в (X, Y) координатной плоскости. За исключением добавленных многогранных поверхностей, эти структуры не отличаются от опубликованных в ранних версиях данной спецификации.


<point> ::= <x> <y>
<geometry tagged text> ::= <point tagged text>
| <linestring tagged text>
| <polygon tagged text>
| <triangle tagged text>
| <polyhedralsurface tagged text>
| <tin tagged text>
| <multipoint tagged text>
| <multilinestring tagged text>
| <multipolygon tagged text>
| <geometrycollection tagged text>
<point tagged text> ::= <point text>
<linestring tagged text> ::= linestring <linestring text>
<polygon tagged text> ::= polygon <polygon text>
<polyhedralsurface tagged
text> ::=		 polyhedralsurface
<polyhedralsurface text>
<triangle tagged text> ::= triangle <polygon text>
<tin tagged text> ::= tin <polyhedralsurface text>
<multipoint tagged text> ::= multipoint <multipoint text>
<multilinestring tagged text> ::= multilinestring
<multilinestring text>
<multipolygon tagged text> ::= multipolygon <multipolygon text>
<geometrycollection tagged
text> ::=		 geometrycollection
<geometrycollection text>
<point text> ::= <empty set>|<left paren>
<point> <right paren>
<linestring text> ::= <empty set> | <left paren>
<point>
{<comma> <point>}*
<right paren>
<polygon text> ::= <empty set> | <left paren> <linestring text>
{<comma> <linestring text>}*
<right paren>
<polyhedralsurface text> ::= <empty set> | <left paren>
<polygon text>
{<comma> <polygon text>}*
<right paren>
<multipoint text> ::= <empty set> | <left paren>
<point text>
{<comma> <point text>}*
<right paren>
<multilinestring text> ::= <empty set> | <left paren>
<linestring text>
{<comma> <linestring text>}*
<right paren>
<multipolygon text> ::= <empty set> | <left paren>
<polygon text>
{<comma> <polygon text>}*
<right paren>
<geometrycollection text> ::= <empty set> | <left paren>
<geometry tagged text>
{<comma> <geometry tagged text>}*
<right paren>

1.2.3 BNF-описание для Трехмерной WKT Геометрии

Этот BNF определяет геометрию в трехмерных (X, Y, Z) координатах.


<point z> ::= <x> <y> <z>
<geometry z tagged text> ::= <point z tagged text>
|<linestring z tagged text>
|<polygon z tagged text>
|<polyhedralsurface z tagged text>
|<triangle tagged text>
|<tin tagged text>
|<multipoint z tagged text>
|<multilinestring z tagged text>
|<multipolygon z tagged text>
|<geometrycollection z tagged text>
<point z tagged text> ::= point z <point z text>
<linestring z tagged text> ::= linestring z <linestring z text>
<polygon z tagged text> ::= polygon z <polygon z text>
<polyhedralsurface z tagged
text> ::=		 polyhedralsurface z
<polyhedralsurface z text>
<triangle z tagged text> ::= triangle z <polygon z text>
<tin z tagged text> tin z <polyhedralsurface z text>
<multipoint z tagged text> ::= multipoint z <multipoint z text>
<multilinestring z tagged
text> ::=		 multilinestring z <multilinestring z text>
<multipolygon z tagged text> ::= multipolygon z <multipolygon z text>
<geometrycollection z tagged
text> ::=		 geometrycollection z
<geometrycollection z text>
<point z text> ::=
<right paren>		 <empty set> | <left paren> <point z>
<linestring z text> ::= <empty set> | <left paren> <point z>
{<comma> <point z>}*
<right paren>
<polygon z text> ::= <empty set> | <left paren>
<linestring z text>
{<comma> <linestring z text>}*
<right paren>
<polyhedralsurface z text> ::= <empty set>|<left paren>
<polygon z text>
{<comma> <polygon z text>}*
<right paren>
<multipoint z text> ::= <empty set> | <left paren>
<point z text>
{<comma> <point z text>}*
<right paren>
<multilinestring z text> ::= <empty set> | <left paren>
<linestring z text>
{<comma> <linestring z text>}*
<right paren>
<multipolygon z text> ::= <empty set> | <left paren>
<polygon z text>
{<comma> <polygon z text>}*
<right paren>
<geometrycollection z text> ::= <empty set> | <left paren>
<geometry tagged z text>
{<comma> <geometry tagged z text>}*
<right paren>

1.2.4 BNF-определение для Двухмерной WKT Геометрии с положением в линейной системе координат)

Данный BNF определяет двумерную геометрию в (X, Y) координатной плоскости. Дополнительно, каждая координата имеет ординату "m", которая является частью некоторой линейной системы координат.


<point m> ::= <x> <y> <m>
<geometry m tagged text> ::= <point m tagged text>
|<linestring m tagged text>
|<polygon m tagged text>
|<polyhedralsurface m tagged text>
|<triangle tagged m text>
|<tin tagged m text>
|<multipoint m tagged text>
|<multilinestring m tagged text>
|<multipolygon m tagged text>
|<geometrycollection m tagged text>
<point m tagged text> ::= point m <point m text>
<linestring m tagged text> ::= linestring m <linestring m text>
<polygon m tagged text> ::= polygon m <polygon m text>
<polyhedralsurface m tagged
text> ::=		 polyhedralsurface m
<polyhedralsurface m text>
<triangle m tagged text> ::= triangle m <polygon m text>
<tin m tagged text> ::= tin m <polyhedralsurface m text>
<multipoint m tagged text> ::= multipoint m <multipoint m text>
<multilinestring m tagged
text> ::=		 multilinestring m <multilinestring m text>
<multipolygon m tagged text> ::= multipolygon m <multipolygon m text>
<geometrycollection m tagged
text> ::=		 geometrycollection m
<geometrycollection m text>
<point m text> ::= <empty set> | <left paren>
<point m>
<right paren>
<linestring m text> ::= <empty set> | <left paren>
<point m>
{{<comma> <point m>}+
<right paren>
<polygon m text> ::= <empty set> | <left paren>
<linestring m text>
{<comma> <linestring m text>}*
<right paren>
<polyhedralsurface m text> ::= <empty set> | <left paren>
<polygon m text>
{<comma> <polygon m text>}*
<right paren>
<multipoint m text> ::= <empty set> | <left paren> <point m text>
{<comma> <point m text>}*
<right paren>
<multilinestring m text> ::= <empty set> | <left paren>
<linestring m text>
{<comma> <linestring m text>}*
<right paren>
<multipolygon m text> ::= <empty set> | <left paren>
<polygon m text>
{<comma> <polygon m text>}*
<right paren>
<geometrycollection m text> ::= <empty set> | <left paren>
<geometry tagged m text>
{<comma> <geometry tagged m text>}*
<right paren>

1.2.5 BNF-описание для Трехмерной WKT Геометрии с положением в линейной системе координат)

Данный BNF определяет трехмерную геометрию в (X, Y, Z) координатной плоскости. Дополнительно, каждая координата имеет ординату "m", которая является частью некоторой линейной системы координат.


<point zm> ::= <x> <y> <z> <m>
<geometry zm tagged text> ::= <point zm tagged text>
|<linestring zm tagged text>
|<polygon zm tagged text>
|<polyhedralsurface zm tagged text>
|<triangle zm tagged text>
|<tin zm tagged text>
|<multipoint zm tagged text>
|<multilinestring zm tagged text>
|<multipolygon zm tagged text>
|<geometrycollection zm tagged text>
<point zm tagged text> ::= point zm <point zm text>
<linestring zm tagged text> ::= linestring zm <linestring zm text>
<polygon zm tagged text> ::= polygon zm <polygon zm text>
<polyhedralsurface zm tagged
text> ::=		 polyhedralsurface zm
<polyhedralsurface zm text>
<triangle zm tagged text> ::= triangle zm <polygon zm text>
<tin zm tagged text> tin zm <polyhedralsurface zm text>
<multipoint zm tagged text> ::= multipoint zm <multipoint zm text>
<multipoint zm tagged text> ::= multipoint zm <multipoint zm text>
<multilinestring zm tagged
text> ::=		 multilinestring zm
<multilinestring zm text>
<multipolygon zm tagged text> ::= multipolygon zm <MultiPolygon zm text>
<geometrycollection zm tagged
text> ::=		 geometrycollection zm
<geometrycollection zm text>
<point zm text> ::= <empty set> | <left paren> <point zm>
<right paren>
<linestring zm text> ::= <empty set> | <left paren>
<point z>
{<comma> <point z>}*
<right paren>
<polygon zm text> ::= <empty set> | <left paren>
<linestring zm text>
{<comma> <linestring zm text>}*
<right paren>
<polyhedralsurface zm text> ::= <empty set> | <left paren> {
<polygon zm text
{<comma> <polygon zm text>}*)
<right paren>
<multipoint zm text> ::= lt;empty set> | <left paren>
<point zm text>
{<comma> <point zm text>}*
<right paren>
<multilinestring zm text> ::= <empty set> | <left paren>
<linestring zm text>
{<comma> <linestring zm text>}*
<right paren>
<multipolygon zm text> ::= <empty set> | <left paren>
<polygon zm text>
{<comma> <polygon zm text>}*
<right paren>
<geometrycollection zm text> ::= <empty set> | <left paren>
<geometry tagged zm text>
{<comma> <geometry tagged zm text>}*
<right paren>

1.2.6 Примеры

Примеры текстового представления Геометрии приведены в Таблице 2. Координаты представляют собой целочисленные значения; они также могут принимать любые значения с двойной точностью.

Примечание:
Примеры POINTZ, POINTM и POINTZM приведены внизу таблицы 6. Этот же способ различения 2D/3D точек и 2D/3D точек с координатой М может быть использован для типов LINESTRING, POLYGON, MULTIPOINT, MULTILINESTRING, MULTIPOLYGON и GEOMETRYCOLLECTION.

Таблица 1 - Примеры Текстового представления геометрии
Тип геометрии Текстовое представление Комментарий
Point Point (10 10) Точка
LineString LineString (10 10, 20 20, 30 40) Ломаная линия из 3 точек
Polygon Polygon (
(10 10, 10 20, 20 20, 20 15, 10 10)) 		Полигон с 1 внешним кольцом и 0 внутренним кольцом
MiltiPoint MultiPoint ((10 10), (20 20)) Мультиточка из 2 точек
MultiLineString MultiLineString ((10 10, 20 20),
(15 15, 30 15))		 Ломаная мультилиния из 2 ломаных линий
MultiPolygon MultiPolygon (
((10 10, 10 20, 20 20, 20 15, 10 10)),
((60 60, 70 70, 80 60, 60 60)))		 Мультиполигон, состоящий из 2 полигонов
GeomCollection GeometryCollection (
POINT (10 10),
POINT (30, 30),
LINESTRING (15 15, 20 20))		 Коллекция, содержащая 2 точечных объекта и 1 ломаную линию
PolyhedralSurface PolyhedralSurface Z
(((0 0 0, 0 0 1, 0 1 1, 0 1 0, 0 0 0)),
((0 0 0, 0 1 0, 1 1 0, 1 0 0, 0 0 0)),
((0 0 0, 1 0 0, 1 0 1, 0 0 1, 0 0 0)),
((1 1 0, 1 1 1, 1 0 1, 1 0 0, 1 1 0)),
((0 1 0, 0 1 1, 1 1 1, 0 1 1, 0 0 1)),
((0 0 1, 1 0 1, 1 1 1, 0 1 1, 0 0 1)))		 Многогранный куб, начальный угол с координатами (0, 0, 0), противоположный - (1, 1, 1)
Tin Tin Z (((0 0 0, 0 0 1, 0 1 0, 0 0 0)),
((0 0 0, 0 1 0, 1 0 0, 0 0 0)),
((0 0 0, 1 0 0, 0 0 1, 0 0 0)),
((1 0 0, 0 1 0, 0 0 1, 1 0 0)))		 Тетраэдр (4 треугольные грани)
Point Point Z (10 10 5) 3D точка
Point Point ZM (10 10 5 40) 3D точка со значением М 40
Point Point M (10 10 40) 2D точка со значением М 40


2. БИНАРНОЕ ПРЕДСТАВЛЕНИЕ ГЕОМЕТРИИ (WKB)

2.1 Обзор

Бинарное Представление Геометрии (WKBGeometry) предусматривает доступное представление геометрического объекта как непрерывный поток байтов. Это позволяет выполнять обмен геометрическими объектами между SQL/CLT клиентом и SQL-реализацией в бинарной форме.

2.2 Описание

2.2.1 Представление

WKB-представление Геометрии получается преобразованием геометрического объекта как последовательности числовых типов, отрисованных из набора {Unsigned Integer, Double} и последующим преобразовании каждого числового типа в последовательность байтов используя одно из двух правильно определенных, стандартных, бинарных представлений числовых типов (NDR, XDR). Специальная бинарная кодировка (NDR или XDR), используемая для представления геометрии, описана однобайтным тэгом, который предшествует преобразованию байтов. Разница между двумя кодировками геометрии заключается в том, что последовательность байтов кодируется обратным порядком байтов (Big Endian) в XDR и прямым порядком байтов (Little Endian) в NDR.

2.2.2 Определение числового типа

Unsigned Integer – 32-битный (4-байтный) тип данных, который кодируется как неотрицательное целое число в интервале [0, 4, 294, 967, 295].

Double – 64-битный (8-байтный) тип данных двойной точности, который кодируется числами двойной точности с использованием IEEE формата двойной точности 754[18]. Эти определения являются общими для XDR и NDR.

2.2.3 Общий список кодов типов геометрии

В этой и других главах спецификации тип геометрии идентифицирован целыми кодами (integer codes). Для одновременного хранения таких кодов и резервирования секций для дальнейшего использования был описан список всех типов геометрических объектов данной спецификации или запланированных реализовать в дальнейшем. Ниже приведена таблица, в которой затененными представлены коды, реализация которых предусмотрена в будущем и которые не используют описанные в спецификации типы.

Таблица 2 - Целые коды типов объектов
Type Code
Geometry 0
Point 1
LineString 2
Polygon 3
MultiPoint 4
MultiLineString 5
MultiPolygon 6
GeometryCollection 7
CircularString 8
CompoundCurve 9
CurvePolygon 10
MultiCurve 11
MultiSurface 12
Curve 13
Surface 14
PolyhedralSurface 15
TIN 16
Type Code
Geometry Z 1000
Point Z 1001
LineString Z 1002
Polygon Z 1003
MultiPoint Z 1004
MultiLineString Z 1005
MultiPolygon Z 1006
GeometryCollection Z 1007
CircularString Z 1008
CompoundCurve Z 1009
CurvePolygon Z 1010
MultiCurve Z 1011
MultiSurface Z 1012
Curve Z 1013
Surface Z 1014
PolyhedralSurface Z 1015
TIN Z 1016
Type Code
Geometry M 2000
Point M 2001
LineString M 2002
Polygon M 2003
MultiPoint M 2004
MultiLineString M 2005
MultiPolygon M 2006
GeometryCollection M 2007
CircularString M 2008
CompoundCurve M 2009
CurvePolygon M 2010
MultiCurve M 2011
MultiSurface M 2012
Curve M 2013
Surface M 2014
PolyhedralSurface M 2015
TIN M 2016
Type Code
Geometry ZM 3000
Point ZM 3001
LineString ZM 3002
Polygon ZM 3003
MultiPoint ZM 3004
MultiLineString ZM 3005
MultiPolygon ZM 3006
GeometryCollection ZM 3007
CircularString ZM 3008
CompoundCurve ZM 3009
CurvePolygon ZM 3010
MultiCurve ZM 3011
MultiSurface ZM 3012
Curve ZM 1013
Surface ZM 3014
PolyhedralSurface ZM 3015
TIN ZM 3016

2.2.4 XDR (Big Endian) кодирование числовых типов

XDR-представление Unsigned Integer заключается в обратном порядке байтов.

XDR-представление Double заключается в обратном порядке байтов.

2.2.5 NDR (Little Endian) кодирование числовых типов

NDR-представление Unsigned Integer заключается в прямом порядке байтов.

NDR-представление Double заключается в прямом порядке байтов.

2.2.6 Преобразования между типами NDR и XDR

Преобразования между типами NDR и XDR для Unsigned Integer и Double является простой операцией обращения порядка байтов в каждом Unsigned Integer или Double в представлении.

2.2.7 Взаимосвязь с протоколами передачи данных COM и CORBA

Описанное выше XDR-представление для Unsigned Integer и Double является так же стандартным представлением для Unsigned Integer и Double в CORBA Standard Stream Format для Externalized Object Data, которое описано как часть CORBA Externalization Service Specification [15].

NDR-представление Unsigned Integer и Double, описанное выше, так же является стандартом представления для Unsigned Integer и Double чисел в протоколах DCOM, основанных на DCE RPC и NDR [16].

2.2.8 Описание представления WKB-Геометрии

В этой главе описывается Бинарное Представление Геометрии. Основным составляющим элементом является представление точки, состоящей из чисел Doubles, которое зависит от системы координат, принятой для отображения геометрии. Представление других геометрических объектов базируется на использовании уже описанных представлений.


// Basic Type definitions
// byte : 1 byte
// uint32 : 32 bit unsigned integer (4 bytes)
// double : double precision number (8 bytes)

// Building Blocks : Coordinate, LinearRing
Point {
   double x;
   double y}

PointZ{
   double x;
   double y;
   double z}

PointM {
   double x;
   double y;
   double m}

PointZM {
   double x;
   double y;
   double z;
   double m}

LinearRing {
   uint32 numPoints;
   Point points[numPoints]}

LinearRingZ {
   uint32 numPoints;
   PointZ points[numPoints]}

LinearRingM {
   uint32 numPoints;
   PointM points[numPoints]}

LinearRingZM {
   uint32 numPoints;
   PointZM points[numPoints]}

enum WKBByteOrder {
   wkbXDR = 0, // Big Endian
   wkbNDR = 1, // Little Endian
}

enum WKBGeometryType {
               wkbPoint= 1,
               wkbLineString= 2,
               wkbPolygon= 3,
               wkbTriangle= 17,
               wkbMultiPoint= 4,
               wkbMultiLineString= 5,
               wkbMultiPolygon= 6,
               wkbGeometryCollection= 7,
               wkbPolyhedralSurface= 15,
               wkbTIN

= 16

               wkbPointZ= 1001,
               wkbLineStringZ= 1002,
               wkbPolygonZ= 1003,
               wkbTrianglez= 1017,
               wkbMultiPointZ= 1004,
               wkbMultiLineStringZ= 1005,
               wkbMultiPolygonZ = 1006,
               wkbGeometryCollectionZ= 1007,
               wkbPolyhedralSurfaceZ= 1015,
               wkbTINZ

= 1016

               wkbPointM= 2001,
               wkbLineStringM= 2002,
               wkbPolygonM= 2003,
               wkbTriangleM= 2017
               wkbMultiPointM= 2004,
               wkbMultiLineStringM= 2005,
               wkbMultiPolygonM= 2006,
               wkbGeometryCollectionM= 2007,
               wkbPolyhedralSurfaceM= 2015,
               wkbTINM

= 2016,

               wkbPointZM= 3001,
               wkbLineStringZM= 3002,
               wkbPolygonZM= 3003,
               wkbTriangleZM= 3017,
               wkbMultiPointZM= 3004,
               wkbMultiLineStringZM= 3005,
               wkbMultiPolygonZM= 3006,
               wkbGeometryCollectionZM= 3007,
               wkbPolyhedralSurfaceZM= 3015,
               wkbTinZM = 3016,
               }

WKBPoint {
   byte byteOrder;
   static uint32 wkbType = 1;
   Point point}

WKBPointZ {
   byte byteOrder;
   static uint32 wkbType = 1001;
   PointZ point}

WKBPointM {
   byte byteOrder;
   static uint32 wkbType = 2001;
   PointM point}

WKBPointZM {
   byte byteOrder;
   static uint32 wkbType = 3001;
   PointZM point}

WKBLineString {
   byte byteOrder;
   static uint32 wkbType = 2;
   uint32 numPoints;
   Point points[numPoints]}

WKBLineStringZ {
   byte byteOrder;
   static uint32 wkbType = 1002;
   uint32 numPoints;
   PointZ points[numPoints]}

WKBLineStringM {
   byte byteOrder;
   static uint32 wkbType = 2002;
   uint32 numPoints;
   PointM points[numPoints]}

WKBLineStringZM {
   byte byteOrder;
   static uint32 wkbType = 3002;
   uint32 numPoints;
   PointZM points[numPoints]}

WKBPolygon {
   byte byteOrder;
   static uint32 wkbType = 3;
   uint32 numRings;
   LinearRing rings[numRings]}

WKBPolygonZ {
   byte byteOrder;
   static uint32 wkbType = 1003;
   uint32 numRings;
   LinearRingZ rings[numRings]}

WKBPolygonM {
   byte byteOrder;
   static uint32 wkbType = 2003;
   uint32 numRings;
   LinearRingM rings[numRings]}

WKBPolygonZM {
   byte byteOrder;
   static uint32 wkbType = 3003;
   uint32 numRings;
   LinearRingZM rings[numRings]}

WKBTriangle {
   byte byteOrder;
   static uint32 wkbType = 17;
   uint32 numRings;
   LinearRing rings[numRings]}

WKBTriangleZ {
   byte byteOrder;
   static uint32 wkbType = 10 17;
   uint32 numRings;
   LinearRingZ rings[numRings]}

WKBTriangleM {
   byte byteOrder;
   static uint32 wkbType = 20 17;
   uint32 numRings;
   LinearRingM rings[numRings]}

WKBTriangleZM {
   byte byteOrder;
   static uint32 wkbType = 30 17;
   uint32 numRings;
   LinearRingZM rings[numRings]}

WKBPolyhedralSurface {
   byte byteOrder;
   static uint32 wkbType = 15;
   uint32 numPolygons;
   WKBPolygon polygons[numPolygons]}

WKBPolyhedralSurfaceZ {
   byte byteOrder;
   static uint32 wkbType=1015;
   uint32 numPolygons;
   WKBPolygonZ polygons[numPolygons]}

WKBPolyhedralSurfaceM {
   byte byteOrder;
   static uint32 wkbType=2015;
   uint32 numPolygons;
   WKBPolygonM polygons[numPolygons]}

WKBPolyhedralSurfaceZM {
   byte byteOrder;
   static uint32 wkbType=3015;
   uint32 numPolygons;
   WKBPolygonZM polygons[numPolygons]}

WKBTIN {
   byte byteOrder;
   static uint32 wkbType = 16;
   uint32 numPolygons;
   WKBPolygon polygons[numPolygons]}

WKBTINZ {
   byte byteOrder;
   static uint32 wkbType=1016;
   uint32 numPolygons;
   WKBPolygonZ polygons[numPolygons]}

WKBTINM {
   byte byteOrder;
   static uint32 wkbType=2016;
   uint32 numPolygons;
   WKBPolygonM polygons[numPolygons]}

WKBTINZM {
   byte byteOrder;
   static uint32 wkbType=3016;
   uint32 numPolygons;
   WKBPolygonZM polygons[numPolygons]}

WKBMultiPoint {
   byte byteOrder;
   static uint32 wkbType=4;
   uint32 numPoints;
   WKBPoint points[numPoints]}

WKBMultiPointZ {
   byte byteOrder;
   static uint32 wkbType=1004;
   uint32 numPoints;
   WKBPointZ points[numPoints]}

WKBMultiPointM {
   byte byteOrder;
   static uint32 wkbType=2004;
   uint32 numPoints;
   WKBPointM points[numPoints]}

WKBMultiPointZM {
   byte byteOrder;
   static uint32 wkbType=3004;
   uint32 numPoints;
   WKBPointZM points[numPoints]}

WKBMultiLineString {
   byte byteOrder;
   static uint32 wkbType = 5;
   uint32 numLineStrings;
   WKBLineString lineStrings[numLineStrings]}

WKBMultiLineStringZ {
   byte byteOrder;
   static uint32 wkbType = 1005;
   uint32 numLineStrings;
   WKBLineStringZ lineStrings[numLineStrings]}

WKBMultiLineStringM {
   byte byteOrder;
   static uint32 wkbType = 2005;
   uint32 numLineStrings;
   WKBLineStringM lineStrings[numLineStrings]}

WKBMultiLineStringZM {
   byte byteOrder;
   static uint32 wkbType = 3005;
   uint32 numLineStrings;
   WKBLineStringZM lineStrings[numLineStrings]}

WKBMultiPolygon {
   byte byteOrder;
   static uint32 wkbType = 6;
   uint32 numPolygons;
   WKBPolygon polygons[numPolygons]}

WKBMultiPolygonZ {
   byte byteOrder;
   static uint32 wkbType = 1006;
   uint32 numPolygons;
   WKBPolygonZ polygons[numPolygons]}

WKBMultiPolygonM {
   byte byteOrder;;
   static uint32 wkbType = 2006;
   uint32 numPolygons;
   WKBPolygonM polygons[numPolygons]}

WKBMultiPolygonZM {
   byte byteOrder;
   static uint32 wkbType = 3006;
   uint32 numPolygons;
   WKBPolygonZM polygons[numPolygons]}

WKBGeometryCollection {
   byte byte_order;
   static uint32 wkbType = 7;
   uint32 numGeometries;
   WKBGeometry geometries[numGeometries]}

WKBGeometryCollectionZ {
   byte byte_order;
   static uint32 wkbType = 1007;
   uint32 numGeometries;
   WKBGeometryZ geometries[numGeometries]}

WKBGeometryCollectionM {
   byte byte_order;
   static uint32 wkbType = 2007;
   uint32 numGeometries;
   WKBGeometryM geometries[numGeometries]}

WKBGeometryCollectionZM {
   byte byte_order;
   static uint32 wkbType = 3007;
   uint32 numGeometries;
   WKBGeometryZM geometries[numGeometries]}

WKBGeometry {Union {
              WKBPoint point;
              WKBLineString linestring;
              WKBPolygon polygon;
              WKBTriangle triangle;
              WKBPolyhedralSurface polyhedralsurface;
              WKBTIN tin;
              WKBMultiPoint mpoint;
              WKBMultiLineString mlinestring;
              WKBMultiPolygon mpolygon;
              WKBGeometryCollection collection;
              }};

WKBGeometryZ {
              union {
              WKBPointZ pointz;
              WKBLineStringZ linestringz;
              WKBPolygonZ polygonz;
              WKBTriangleZ trianglez;
              WKBPolyhedralSurfaceZ Polyhedralsurfacez;
              WKBTinZ tinz;
              WKBMultiPointZ mpointz;
              WKBMultiLineStringZ mlinestringz;
              WKBMultiPolygonZ mpolygonz;
              WKBGeometryCollectionZ collectionz;
              }};

WKBGeometryM {Union {
              WKBPointM pointm;
              WKBLineStringM linestringm;
              WKBPolygonM polygonm;
              WKBTriangleM trianglem;
              WKBPolyhedralSurfaceM Polyhedralsurfacem;
              WKBTinM tinm;
              WKBMultiPointM mpointm;
              WKBMultiLineStringM mlinestringm;
              WKBMultiPolygonM mpolygonm;
              WKBGeometryCollectionM collectionm;
              }};

WKBGeometryZM {Union {
              WKBPointZM pointzm;
              WKBLineStringZM linestringzm;
              WKBPolygonZM polygonzm;
              WKBTriangleZM trianglezm;
              WKBPolyhedralSurfaceM Polyhedralsurfacezm;
              WKBTinZM tinzm;
              WKBMultiPointZM mpointzm;
              WKBMultiLineStringZM mlinestringzm;
              WKBMultiPolygonZ mpolygonzm;
              WKBGeometryCollectionZM collectionzm;
              }};

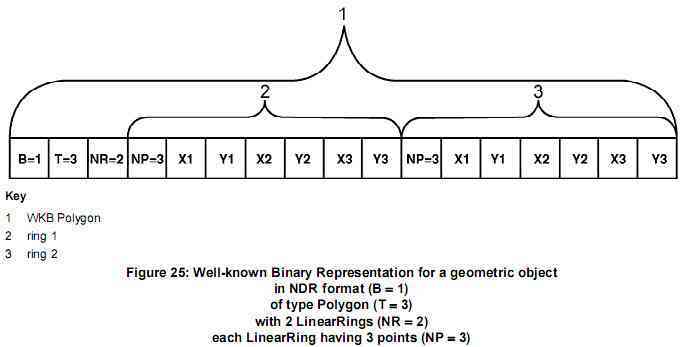
На рисунке 25 показано графическое представление полигона с внешним и внутренним кольцом.

2.2.9 Утверждения для Бинарного Представления Геометрии

Бинарное Представление Геометрии разработано для представления экземпляров Типов Геометрии. Любой экземпляр WKB-Геометрии будет удовлетворять утверждениям, описанным в этой спецификации.

3 ТЕКСТОВОЕ ПРЕДСТАВЛЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ КООРДИНАТ

3.1 Обзор

Текстовое Представление Пространственной Системы Координат предусматривает стандарт текстового представления информации о пространственной системе координат.

3.2 Описание

Пространственная Система Координат, или просто система координат, может быть представлена географической (широта-долгота), плановой (X, Y) или геоцентрической (X, Y, Z) системами координат.

Каждый объект начинается с ключевого слова, записанного в верхнем регистре (например, DATUM или UNIT ), который следует после указанных в квадратных скобках и разделенных запятыми параметров объекта. Если объект состоит из нескольких объектов, результатом является вложенная структура. При реализации должна осуществляться возможность замены стандартных скобок ( ) на квадратные [ ], а так же чтение обоих видов скобок.

Приложение Б содержит список Геодезических Кодов и Параметров для описания объектов в Текстовом Представлении информации о референцной системе координат. Некоторое описание чисел и имен взяты из WKB-Геометрии.


<spatial reference system> ::= <projected cs>|
<geographic cs>|
<geocentric cs>
<projected cs> ::= PROJCS <left delimiter>
<csname>
<comma> <geographic cs>
<comma> <projection>
(<comma> <parameter> )*
<comma> <linear unit>
<right delimiter>
<geographic cs> ::= GEOGCS <left delimiter> <csname>
<comma> <datum>
<comma> <prime meridian>
<comma> <angular unit>
(<comma> <linear unit>)
<right delimiter>
<geocentric cs> ::= GEOCCS <left delimiter>
<name>
<comma> <datum>
<comma> <prime meridian>
<comma> <linear unit>
<right delimiter>
<datum> ::= DATUM <left delimiter> <datum name>
<comma> <spheroid>
<right delimiter>
<projection> ::= PROJECTION <left delimiter>
<projection name>
<right delimiter>
<parameter> ::= PARAMETER <left delimiter>
<parameter name>
<comma> <value>
<right delimiter>
<spheroid> ::= SPHEROID <left delimiter>
<spheroid name>
<comma> <semi-major axis>
<comma> <inverse flattening>
<right delimiter>
<prime meridian> ::= PRIMEM <left delimiter>
<prime meridian name>
<comma> <longitude>
<right delimiter>
<linear unit> ::= <unit>
<angular unit> ::= <unit>
<unit> ::= UNIT <left delimiter>
<unit name>
<comma> <conversion factor>
<right delimiter>
<value> ::= <signed numeric literal>
<semi-major axis> ::= <signed numeric literal>
<longitude> ::= <signed numeric literal>
<inverse flattening> ::= <signed numeric literal>
<conversion factor> ::= <signed numeric literal>
<unit name> ::= <quoted name>
<spheroid name> ::= <quoted name>
<projection name> ::= <quoted name>
<prime meridian name> ::= <quoted name>
<parameter name> ::= <quoted name>
<datum name> ::= <quoted name>
<csname> ::= <quoted name>

Примечание:
Большая полуось измеряется в метрах и должна быть больше нуля.
Примечание:
Коэффициент преобразования устанавливает число метров (для линейных измерений) и ли число радиан (для угловых измерений) на единицу. Коэффициент преобразования должен быть больше нуля.

Система координат набора данных идентифицирована в ключевом слове PROJCS если данные заданы в плановых координатах, GEOGCS - в географических и GEOCCS –в геоцентрических.

Ключевое слово PROJCS следует за всеми «частями», которые заданы в плановой системе координат. Первой частью любого объекта является имя. Несколько объектов соответствуют плановой системе координат: географическая система координат, картографическая проекция, 0 или более параметров и линейные единицы измерения. Все плановые системы координат основаны на географических системах координат, поэтому специфичные для плановой системы координат части должны быть описаны в первую очередь.

ПРИМЕР 1: Описание зоны 10N UTM в датуме NAD83:

PROJCS["NAD_1983_UTM_Zone_10N",
<geographic cs>,
PROJECTION["Transverse_Mercator"],
PARAMETER["False_Easting",500000.0],
PARAMETER["False_Northing",0.0],
PARAMETER["Central_Meridian",-123.0],
PARAMETER["Scale_Factor",0.9996],
PARAMETER["Latitude_of_Origin",0.0],
UNIT["Meter",1.0]]

Имя и некоторые объекты описывают географическую систему координат по очереди: датум, эллипсоид, начальный меридиан, угловые единицы измерений.

ПРИМЕР 2: Строковое описание географической системы координат зоны 10N UTM в NAD83

GEOGCS["GCS_North_American_1983",
DATUM["D_North_American_1983",
ELLIPSOID["GRS_1980",6378137,298.257222101]],
PRIMEM["Greenwich",0],
UNIT["Degree",0.0174532925199433]]

ПРИМЕР 3: Полное строковое представление зоны 10N UTM

PROJCS["NAD_1983_UTM_Zone_10N",
GEOGCS["GCS_North_American_1983",
DATUM[ "D_North_American_1983",ELLIPSOID["GRS_1980",6378137,298.257222101]],
PRIMEM["Greenwich",0],UNIT["Degree",0.0174532925199433]],
PROJECTION["Transverse_Mercator"],PARAMETER["False_Easting",500000.0],
PARAMETER["False_Northing",0.0],PARAMETER["Central_Meridian",-123.0],
PARAMETER["Scale_Factor",0.9996],PARAMETER["Latitude_of_Origin",0.0],
UNIT["Meter",1.0]]


Copyright © 2006 Open Geospatial Consortium, Inc. All Rights Reserved.
Наверх | Библиотека
© ДонНТУ 2009 Григорива Ольга