Источник: www.old.appraiser.ru/info/method/anisimova.doc
Анисимова Ирина Николаевна
доцент Санкт-Петербургского Инженерно-экономического университета
Баринов Николай Петрович
ген. директор ООО "ОФ "БОСИ"
Грибовский Сергей Викторович
зам. нач. ГУ ГУИОН СПб
О ТРЕБОВАНИЯХ К КОЛИЧЕСТВУ СОПОСТАВИМЫХ ОБЪЕКТОВ ПРИ ОЦЕНКЕ НЕДВИЖИМОСТИ СРАВНИТЕЛЬНЫМ ПОДХОДОМ
С развитием отечественного рынка недвижимости все большее значение приобретают методы сравнительного подхода к оценке типовых объектов, каждый из которых можно рассматривать как сопоставимый с однородной группой объектов, представленных на рынке. В оценке недвижимости уже не является новинкой моделирование рынка методами многомерного корреляционно-регрессионного анализа. Примеры использования этого мощного математического аппарата при оценке недвижимости вошли в учебники по эконометрике [1,2] и оценке [3], им посвящены публикации в периодических изданиях [4, 5,6], появилась и первая монография на русском языке [7]. Наконец, более пяти лет в Санкт-Петербурге успешно применяется Методика определения арендной платы за нежилые помещения, построенная по результатам статистического моделирования городского рынка арендных ставок методами множественной регрессии.
Тем не менее, при решении практических задач индивидуальной оценки объектов недвижимости хорошо разработанные теоретически, легко реализуемые на современных компьютерах и достаточно объективные модели множественной регрессии используются лишь узким кругом российских оценщиков. На наш взгляд, это связано не столько с молодостью оценочной деятельности в современной России и относительной неразвитостью рынка, сколько с отсутствием каких-либо обоснованных требований к объему выборки рыночных данных, необходимому для решения задач оценки методами регрессионного анализа. Или, другими словами, остается неясным сколько аналогов (сопоставимых объектов) необходимо использовать при расчете рыночной стоимости объекта недвижимости методом сравнительного анализа рыночных данных.
Действительно, сегодня для построения надежной эконометрической модели рекомендуют [1, 7, 10] использовать объем выборки рыночных данных, равный 5-7 – кратному числу используемых моделью независимых факторных переменных (ценообразующих факторов). Применительно к наиболее распространенным значениям числа основных влияющих факторов – 4-7, позволяющих строить адекватные модели для отдельных сегментов рынка недвижимости, необходимый объем выборки однородных рыночных данных должен составлять в этом случае порядка 25-50 сделок или предложений к ним. Опыт показывает, что это слишком жесткое требование для пассивных рынков российских поселений, за исключением, может быть, таких городов как Москва, Петербург, Екатеринбург, Нижний Новгород и некоторые другие.
Но можно ли рассматривать данную рекомендацию и вытекающие из нее требования к объему выборки как минимально достаточные для решения практической задачи индивидуальной оценки объекта недвижимости? Мы полагаем, что нет, т.к. реально потребный объем выборки для решения данной задачи может быть существенно меньше. Покажем это.
Требование 5-7-кратного превышения объемом выборки числа факторных переменных призвано обеспечить значимость не только регрессионного уравнения в целом, но также и каждого из коэффициентов регрессии. Практическая ценность значимости коэффициентов регрессии заключается в выявлении характера влияния каждого из факторов на исследуемую величину (результирующий признак). Вскрытие закономерностей, т.е. характера взаимосвязей между результирующим признаком и влияющими факторами в классической эконометрической постановке задачи статистического моделирования зачастую является главной целью исследования, т.к. призвано обеспечить возможность формирования количественно обоснованного управляющего воздействия на тот или иной влияющий фактор для придания результирующему признаку заданных значений.
На наш взгляд, выявление тонкой структуры указанных связей применительно к задаче индивидуальной оценки объектов недвижимости является избыточным. Действительно, оценщик, проводя расчет рыночной стоимости (или ставки аренды) конкретного здания, помещения или земельного участка, не решает задачи иной, чем количественное определение суммарного результирующего влияния основных ценообразующих факторов на формирование цены (арендной ставки) данного объекта. При этом на практике почти всегда наблюдается частичная мультиколлинеарность; влияющих факторов, которая, порою, сводит к минимуму значимость влияния каждого из факторов на выходную величину. Напомним, что наличие частичной мультиколлинеарности факторных переменных при выполнении остальных предпосылок линейной регрессии не смещает оценку среднего, а лишь ухудшает качество интервальной оценки [см., например, 1,2,8].
Таким образом, для решения задачи индивидуальной оценки объекта недвижимости сравнительным подходом достаточным, на наш взгляд, условием адекватности полученной модели множественной регрессии может являться статистическая значимость уравнения в целом (при этом предполагается выполнение условий, обеспечивающих получение несмещенных оценок, обсуждение которых мы откладываем до следующих публикаций).
Статистическая значимость линейного регрессионного уравнения в целом проверяется с помощью статистики Фишера, критические значения Fkr которой зависят от числа используемых факторов-регрессоров k, объема выборки n, а также заданного уровня значимости. Процедура сводится к проверке нуль-гипотезы о том, что, ни один из факторов, включенных в модель, не оказывает существенного влияния на результирующий показатель. Если расчетное значение F-критерия превышает критическое, то гипотеза о несоответствии используемых в модели связей реально существующим отвергается, и считается, что уравнение в целом статистически значимо и хорошо соответствует рыночным данным.
Расчетное значение F-критерия определяется как
Fр=R²(n-k-1)/k(1-R²)
где R²– коэффициент детерминации (квадрат коэффициента множественной корреляции):
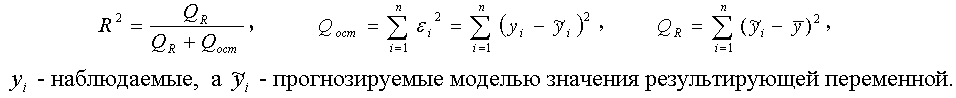
Критические значения F-критерия определяются по таблицам (публикуемым в литературе или электронным) при заданном уровне значимости (в экономических задачах широко используется значение 0,05) и числе степеней свободы υ1=k, υ2=n-k-1.
Обратим внимание на связь расчетного значения F-критерия со значением коэффициента детерминации R², который в свою очередь часто используется для оценки качества применяемой модели, т.к. характеризует долю дисперсии, объясняемую моделью, в общей дисперсии результирующего признака. В практических задачах оценка качества модели по показателю R² считается весьма высокой, если его значения достигают значений 0,9 и выше, и вполне достаточной при значениях ≥ 0,7. Из выражения (1) для F-критерия легко заметить, что его расчетное значение растет с ростом объема выборки и коэффициента детерминации. С другой стороны, критическое значение критерия при заданном уровне значимости и числе используемых моделью влияющих факторов падает с ростом объема выборки. Таким образом, в предположении, что будет обеспечено требуемое качество модели, отражаемое значением коэффициента детерминации, всегда можно указать минимальный объем выборки, начиная с которого расчетное значение критерия будет превышать критическое.
Интуитивно понятно, что объем выборки и «качество» модели являются обменными величинами. Так, например, если бы перед оценщиком стояла задача определения рыночной стоимости единицы площади квартиры без отделки в строящемся с привлечением средств инвесторов типовом многоквартирном доме, то, скорее всего, ему достаточно было бы знать значение цены этой площади, указанное в оферте девелопера. А наличие трех (вполне возможно, очень близких) значений из заключенных договоров инвестирования строительства не вызывало бы никаких вопросов, кроме быть может, о скидках в цене квартир последнего этажа. В данном случае, все объекты можно считать практически одинаковыми по уровням основных влияющих факторов, и адекватной моделью стоимости является, скорее всего, среднее по выборке цен значение.
При использовании объектов-аналогов, отличающихся от оцениваемого объекта уровнями по нескольким основным ценообразующим факторам, «качество» модели зависит как от степени этих отличий, так и от спецификации модели, т.е. адекватности моделируемого характера зависимостей результирующего показателя (стоимости, ставки аренды) от факторов-регрессоров. В отличие от задач массовой оценки, первая составляющая – размах отклонений значений влияющих факторов объектов-аналогов от соответствующих значений оцениваемого объекта – является, в определенной степени, управляемой величиной. Другими словами, оценщик формирует контролируемую выборку данных, следя за тем, чтобы в нее попали наиболее близкие к объекту по значениям основных ценообразующих факторов (но не по стоимости!) аналоги. Здесь нет необходимости останавливаться на проблемах такого отбора и методах их решения, т.к. одни частично освещены (см., например [9]), другие требуют более подробного рассмотрения, которое мы отложим на будущее. Отметим только, что при одном и том же объеме выборки ее однородность, плотность группирования вокруг оцениваемого объекта может быть различной, что во многом определит и статистические свойства модели.
Важно отметить, что в результате статистического моделирования должно быть получено значимое уравнение множественной регрессии с достаточно высокими показателями достоверности, чтобы результаты расчета по ней могли претендовать на использование в отчете об оценке. Как уже отмечалось, одним из используемых показателей адекватности уравнения является коэффициент детерминации, нижней границей значений которого при решении задачи индивидуальной оценки может быть принята величина 0,7.
Можно задать следующий вопрос: если предположить, что отобранные аналоги обеспечат после проведения моделирования уровень коэффициента детерминации не менее 0,7, какое количество таких аналогов необходимо найти на рынке, чтобы обеспечить статистическую значимость регрессионного уравнения? А если однородность выборки и спецификация модели обеспечит значения коэффициента детерминации 0,8 или 0,9?
Ответы на эти вопросы для классической линейной множественной регрессии могут быть легко получены сравнением расчетного F[R²] и критического Fkr значений F-критерия при заданных уровне значимости (0,05), числе используемых моделью факторов-регрессоров и объеме выборки (см. таблицы расчетов). Для наглядности сравнения результатов объем n выборки выражен через дополнение к числу k используемых в модели факторных переменных.

В затемненных областях таблиц представлены расчетные значения F-критерия, достигающие и превышающие соответствующие критические его значения. Анализ полученных результатов для моделей, использующих число факторных переменных от k=3 до k=7 включительно, позволяет сделать следующие обобщения.
Для получения представляющих практический интерес результатов моделирования цены (ставки аренды) оцениваемого объекта недвижимости методами множественной линейной регрессии по выборке рыночных данных о ценах (арендных ставках) его аналогов, необходимо иметь в распоряжении, как минимум, n=2(k+2) аналогов оцениваемого объекта. Такой объем выборки достаточен при требуемом уровне коэффициента детерминации R²≥0,7.
Если отличия в характеристиках объекта оценки и отобранных аналогах достаточно малы и модель хорошо специфицирована (коэффициент детерминации R²≥0,8), потребный объем выборки может быть оценен значением n=2(k+1).
При наличии на рынке очень близких аналогов и верной спецификации модели (R²≥0,9) для статистической значимости регрессионного уравнения достаточно иметь объем выборки, равный n=k+5.
Таблица сравнения требуемых объемов выборки рыночных данных

Опыт практического моделирования сегментов рынка коммерческой недвижимости в Санкт-Петербурге при решении задач индивидуальной оценки показывает, что существующее состояние рынка позволяет формировать выборки из объектов-аналогов, обеспечивающие получение значений коэффициента детерминации не ниже 0,8. Это означает, что для наиболее часто применяемых моделей с числом факторов 4-5 статистическая значимость уравнения обеспечивается уже при объеме выборки, содержащем 10-12 аналогов соответственно. При удовлетворении существующих рекомендаций потребовалось бы формировать выборку из 25-30 аналогов, что для большинства оцениваемых объектов пока невыполнимо. Отметим попутно, что с повышением однородности выборки (близости аналогов к объекту оценки) растет и адекватность применения собственно линейной модели регрессии.
Полученные соотношения, определяющие минимально достаточный объем выборки, не носят абсолютного характера, так как базируются на классической параметрической модели линейной регрессии с ее основными предпосылками. Тем не менее, эти оценки подтверждаются практикой моделирования и существенно расширяют область применения методов аппарата множественной регрессии при решении задач индивидуальной оценки объектов недвижимости на отечественном рынке.
Выводы
ЛИТЕРАТУРА
Опубликовано: Вопросы оценки. Научно-практический журнал. М.: РОО, 2003, №1, с.2-7