МОДЕЛЬ СТАЦИОНАРНОГО ТЕПЛОВОГО АНАЛИЗА В СРЕДЕ ANSYS

Нестеренко Р.Б., студент 2 курса; Казакова Е.И., д-р техн. наук, проф.
Донецкий национальный технический университет

Источник: Прикладные задачи математики в механике, экологии — 2006 / ІV международной студенческой конференции — Севастополь, СевНТУ — 2006

В настоящее время в научных исследованиях и при решении различного рода прикладных задач все большая роль отводится компьютерному математическому моделированию. Среди средств обеспечения исследований особо важное место занимает комплексная система ANSYS, реализующая метод конечных элементов и позволяющая решать следующие краевые задачи: механики деформируемого твердого тела, расчета полей температуры, динамики жидкости и газа, электромагнитных и акустических полей.
Основой теплового анализа в ANSYS является уравнение теплового баланса, полученное в соответствии с принципом сохранения энергии. В ANSYS реализованы расчетные средства для трех видов теплообмена: кондуктивного, конвективного (свободного и вынужденного) и радиационного. Эти средства используются при проведении стационарного, нестационарного, линейного или нелинейного теплового анализа. Для конечно-элементного представления системы разрешающее уравнение процесса теплопередачи имеет вид:

[C] {T'} + [K] {T} = {Q},

где
[C] – матрица удельных теплоемкостей;
{T'}– производная по времени температуры в узле;
[K]– матрица эффективной теплопроводности;
{T} – вектор узловых температур;
{Q} – вектор эффективного теплового потока в узле.
Рассмотрим порядок построения компьютерной модели стационарного теплового анализа в среде ANSYS на следующем примере: имеется стальная прямоугольная пластина размером 0,75 на 0,5м., в которой вырезано два круглых отверстия диаметром по 0,1м. каждое. На одну из коротких сторон воздействует окружающая среда с температурой 20?, а на противоположную ей сторону - 110 ?
Ставится задача – провести нелинейный тепловой расчет конструкции с получением цветного двухмерного изображения распределения температуры и получение графиков изменения температуры и величины теплового потока по выбранному направлению. На рис.1 приведена блок-схема проведения теплового анализа в ANSYS.

m1

Рис. 1. Блок-схема проведения теплового анализа в среде ANSYS

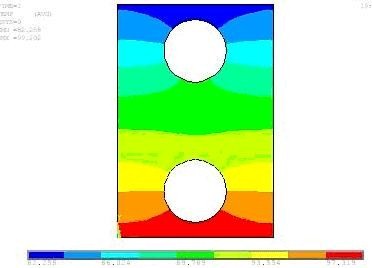
Результаты теплового анализа выводятся в табличной форме и представляют собой значения температуры и плотности теплового потока в узлах. Эти данные могут быть использованы также для построения картины изотерм и получения графиков изменения температуры и величины теплового потока по выбранному направлению. На рис.2 показан результат теплового анализа в графической форме.

m1

Рис. 2. Результат теплового анализа в графической форме

Литература

  1. Басов К.А. ANSYS: справочник пользователя. -М,:ДМК Пресс, 2005.-640 с., ил.
  2. Басов К.А. Графический интерфейс комплекса ANSYS. -М,:ДМК Пресс, 2006.-248 с., ил.