Источник: http://lissov.kiev.ua/guest/publications/iss/Grygorian_Lissov_001_Program_Imitator_Of_Human_CVS.pdf
ПРОГРАММНЫЙ ИМИТАТОР СЕРДЕЧНО-СОСУДИСТОЙ СИСТЕМЫ ЧЕЛОВЕКА НА ОСНОВЕ ЕЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Предложена математическая модель физиологических процессов в сердечно-сосудистой системе (ССС) человека, реализованная в виде программы для теоретических исследований гемодинамики. Насосная функция сердца моделируется на основе асинхронного изменения жесткости клеток миокарда в течение сердечного цикла. Нейрогуморальная регуляция сердца и тонуса сосудов малого и большого кругов кровообращения построена на основе сосудистой механорецепции, хеморецепции, изменения активности высших вегетативных центров, а также с учетом реакции на изменения температуры крови. Реакции ССС на внешние воздействия (гравитационные, барометрические, физическая и эмоциональная нагрузки и др.) отслеживаются в динамике. Программа может быть использована самостоятельно или в составе специальной исследовательской технологии, интегрирующей комплекс физиологически сопряженных моделей при решении научных и некоторых прикладных задач физиологии и медицины.
Введение
Для теоретических и прикладных медико-физиологических исследований количественных закономерностей функционирования сердечно- сосудистой системы (ССС) человека в норме и патологических состояниях вот уже несколько десятилетий используются компьютерные (программные) имитаторы гемодинамики [1-5]. Развитие программных технологий позволяет сделать такие модели все более удобными для пользователя при одновременном наращивании физиологической базы знаний. В идеале экспертам в предметной области хочется иметь такую компьютерную программу, которая сочетала бы в себе простоту и удобство пользования с описанием всех известных физиологических закономерностей. Движение в сторону этого идеала продолжается созданием более полных математических моделей и более привлекательных интерфейсных возможностей.
Предложенная ранее [6,7] новая концепция создания комплексных математических моделей и компьютерных имитаторов физиологических функций человека, основанная на описании функционирования органов в терминах гетерогенных популяций клеток с динамическими свойствами, позволила подойти к проблеме моделирования деятельности любого нашего многоклеточного органа с новой точки зрения. Применительно к насосной функции сердца новый подход заключается в том, что моделирование базируется на учете асинхронности процессов как сокращения, так и расслабления разных кардиомиоцитов одной камеры сердца. Создаются предпосылки для охвата одной моделью практически всего спектра нормального и патологического функционирования сердца, что выгодно отличает такую модель от разработанных ранее. Более того, подход позволяет также моделировать возможные траектории адаптивных трансформаций состояния элементов (кардиомиоцитов) и изменений плотности вероятности их распределения в зависимости от коронарного кровотока. Обладая значительной новизной, такая технология моделирования может способствовать существенному продвижению компьютерных методов в медико- физиологические исследования. Поскольку модель и программный модуль являются составной частью разрабатываемого нами специализированного программно - моделирующего комплекса, предназначенного для теоретических исследований причинно-следственных взаимоотношений в организме человека в процессе его взаимодействия с динамической внешней средой, есть необходимость их самостоятельного детального описания.
Целью настоящей публикации является описание оригинального метода моделирования функции сердца, модели гемодинамики с учетом физиологических механизмов регуляции, а также базового программного имитатора, позволяющего проводить компьютерные имитационные исследования по широкому кругу медико-физиологических проблем кровообращения человека.
Описание математической модели.
Для того чтобы программный имитатор гемодинамики был адекватным исследовательским инструментом, модель должна описывать основные биофизические и физиологические закономерности в следующих компонентах ССС: 1. Насосную деятельность сердца; 2. Гидродинамику в сосудистой сети; 3. Нейрогуморальную регуляцию функции сердца и тонуса сосудов; 4. Воздействия внешних по отношению к ССС факторов на характеристики сердца, сосудов и регуляторных структур. В кибернетических терминах два первых пункта объединяют объект управления, третий пункт соответствует регулятору, а четвертый – среде. Как будет показано ниже, созданная программа позволяет произвести независимую настройку характеристик всех трех выделенных компонентов модели.
Модель насосной функции сердца строится исходя из того, что функциональная роль сердца в целостном организме состоит в увеличении энергии поступающего на вход венозного потока до значений, необходимых для обеспечения последовательной прокачки крови по сети сосудов (артерии, артериолы, капилляры, вены) и возврата к сердцу. При этом достаточно моделировать деятельность желудочков, привязав ее к особенностям динамики входных и выходных клапанов, а также учтя разные гидродинамические сопротивления малого и большого кругов кровообращения. В этом контексте рост энергии потока достигается за счет систолического сокращения кардиомиоцитов данной камеры сердца. Направленный поток крови происходит благодаря закрытия входных и открытия выходных клапанов под влиянием разницы давлений крови по обе стороны клапанных лепестков. После изгнания из желудочка порции крови наступает диастолическая фаза: миокард расслабляется, его жесткость снижается, падает внутреннее давление крови в желудочках, открываются входные клапаны и из вен под разницей давлений поступает новая порция крови. Чередование систолического роста и диастолического спада объемной жесткости правого -Dr(t) и левого- Dl(t) желудочков происходит с периодичностью, задаваемой пейсмекерными клетками синусного узла. Изменения температуры и химизма крови сдвигают величину потенциала покоя этих клеток, модулируя рост или снижение частоты сокращений сердца (ЧСС). Энергетика сердечного сокращения определяется интегральным инотропным состоянием кардиомиоцитов Ir(t), Il(t). Оно зависит от коронарного кровообращения и химических агентов (продуцируемых центральной нервной системой и надпочечниками), потенцирующих или ингибирующих сократительный эффект.
Скорость распространения нервного импульса по проводящей системе
сердца на два порядка превышает скорость развития процесса
электромеханического сопряжения. Это позволило [8] считать, что
асинхронность сокращения кардиомиоцитов внутри их популяции в рамках
данной камеры сердца является основной причиной формирования характерной
динамики подъема жесткости миокарда в систолу. Этот же механизм лежит в
основе формирования динамики диастолического спада жесткости. Как было
показано ранее [9], динамика объемной жесткости желудочков внутри одного
сердечного цикла удобно моделировать с помощью β – функции, определенной
на интервале (0,1) как:
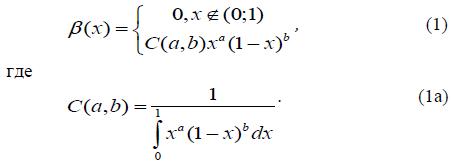
Для этого необходимо ввести связанные с длительностю сердечного
цикла (Tc), фаз систолы (τs) и диастолы ( τd) промежуточные переменные,
определяемые как:
τd = Wd (Tc); τs = Ws (Tc) для задания значений Dr(t) (i=2) и левого Dl(t) (i=5) желудочков в виде общих формул (*).
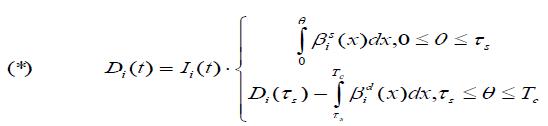
Для моделирования специфической динамики жесткости каждого желудочка в систоле и диастоле согласно (*), необходимо и достаточно иметь 4 пары значений констант a и b в формуле (1) и привязанную к коронарному кровоснабжению характеристику их инотропного состояния Ii(t).
Система уравнений, описывающая динамику объемов Vi(t), давлений Pi(t)
и объемной жесткости - Di(t) соответствующего желудочка сердца, а также
объемной скорости крови Qi(t), задается системой уравнений (3)-(5).

где Ui(t), – ненапряженный объем, Li – постоянная времени,
характеризующая инерционность процесса изменения потока крови на выходе
желудочка в фазу изгнания, а динамика сопротивления входных и выходных
клапанов Riv(t) соответствующих желудочков сердца задается как функция
разности давлений Pi - Pi+1 по обе стороны клапана в виде зависимости:
где δ- константа, характеризующая инерционность процесса открытия клапанов, Rivo, Rivc - гидравлические сопротивления полностью открытого и полностью закрытого клапанов соответственно. Заметим, что простыми изменениями δ, Rivo, Rivc можно имитировать широкий спектр вариаций патологии сердечных клапанов, в том числе и появление регургитации крови.
Таким образом, система уравнений (1) - (6) с учетом формулы (*) представляют собой математическую модель, имитирующую кардиоциклические пульсации давлений, объемов и потоков крови в желудочках сердца.
Гидродинамику в сосудистой сети, представленной в модели в виде
последовательно и параллельно соединенных участков сосудов с
сосредоточенными параметрами, моделируем аналогичными (3) - (5а)
уравнениями с некоторыми модификациями. Прежде всего модификация
относится к рассчетной формуле для кровотоков. Поскольку в нашей модели
сосудистая система представлена состоящей из относительно укрупненных
участков, можно инерционность потока не учитывать и Qi(t) рассчитать по
формуле (5а). Помимо этого, выходные сопротивления сосудистых участков,
зависящие от величины поперечного сечения сосуда, привязаны к значениям их
текущих реальных объемов и ненапряженных объемов, и определяются в
соответствии со следующей формулой:
Формула (7) позволяет избежать парадоксальных ситуаций, нередко имевших место в моделях, основанных на раздельном управлении Di(t), Ui(t) и Ri(t) центральными регуляторами, когда на фоне роста кровенаполнения сосуда возможно увеличение его сопротивления.
Следующая модификация касается формирования гидродвижущих сил. Поскольку некоторые сосудистые участки могут располагаться в полостях или тканях с разными экстрасосудистыми давлениями (следовательно, возникают дополнительные факторы, участвующие в формировании градиентов давлений между участками), каждый участок сосуда имеет также свое независимое экстрасосудистое давление Pi E(t). Другой существенный модификатор гидродвижущих сил – это гидростатическое давление Pi G(t), зависящее от длины столба крови li, угла отклонения от горизонтали φi и величины ускорений a = ng, где n - гравитационная перегрузка: Pi G(t)= ngli sin φi . Таким образом, учет перечисленных дополнений в уравнениях определения скорости вытекающей из сосудистого участка крови позволяет моделировать также реакции ССС на динамические нагрузки ускорениями, гипо- и гипергравитацией, наружным барометрическим локальным, или глобальным давлением. Приложение локального измененного экстрасосудистого давления к сосудистым участкам с сосредоточенными в них механорецепторами порождает двоякий эффект, обусловленный как непосредственным изменением кровенаполнения, также рефлекторным компонентом, вызванным изменением активности рецепторов.
Нейрогуморальную регуляцию функции сердца и тонуса сосудов моделируем с учетом концентраций в крови основных кардио- и вазоактивных веществ - ацетилхолина (СAh), адреналина (СA) и норадреналина (СN). Принято, что изменения СA в крови направлены против изменений артериальной механорецепции (MA), активности волюмрецепторов сердца (Ω),
хеморецепторов (X). Наоборот, высшие вегетативные центры (ВВЦ) оказывают прямое стимулирующее (HS) или угнетающее (HI) влияние на продукцию этих медиаторов. Зависимости для СAh и СA носят реципрокный характер, что отражает регуляцию по отрицательной и положительной обратной связи. Что касается СN, она изменяется однонаправленно с СA , но инерционность ее динамики существенно больше. Математические выражения для моделирования перечисленных выше связей представлены ниже:

где константы a,b,c, εS, εI, Ψ1, Ψ2 отражают количественные различия между состояниями симпатического и парасимпатического отделов вегетативной нервной системы, а последние члены описывают процесс утилизации произведенного медиатора клеточными рецепторами с разными скоростями f1 и f2 для адреналина и ацетилхолина соответственно.
Производство норадреналина надпочечниками инициируется как
непосредственно мозговыми центрами. Наряду с этим установлено [10,11], что
существует положительная корреляция между активностью сердечно-
сосудистых механорецепторов и уровнем СN. За неимением более детальной
физиологической информации, динамику СN в модели представили уравнением,
аналогичным (8), но с учетом значительно большей инерционности как
выделения так и утилизации СN.
Опыт успешного применения [8,9] подхода, в рамках которого
характерную S –образную зависимость кривых, связывающих статический
уровень рецепторной активности (Y) в многоволоконном афферентном нерве с
надпороговым входным стимулом (Z), аппроксимировалась формулой типа:
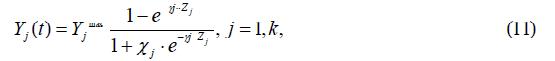
позволил использовать выражение (10) в данной модели как основы для описания дифференциальной формы искомой связи Yj( χj) в динамике кардиоцикла как:
где индекс j относит величины к каждому из k включенных в контур регулирования рефлексогенных зон, а Yjmax, ϒj,χj – константы аппроксимации. При подпороговых значениях входного стимула импульсация в рецепторах отсутствует.
В данном варианте модели k = 3, поскольку рассматриваются всего три
рефлекса (MA, Ω и X). Блок-схема модели представлена на рис. 1.
Регуляция функции сердца включает в себя изменения Tc> и инотропного
состояния правого и/или левого желудочков посредством СAh , СN и СA. Кроме
этого, учтено влияние температуры крови Тк на Tc. Соответствующие
математические выражения выглядят как:
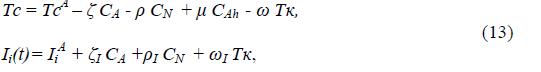
где TcA, Ii A – значения соответствующих переменных при функционировании сердца в режиме автоматизма и нормальных величинах констант аппроксимации Тк, ζ, Ρ, μ, ω, ζI, и ΡI , характеризующих чувствительность TcA и IiA к соответствующим переменным состояния.
Данная разработка ориентирована на решение задач не только из области быстрой рефлекторной регуляции гемодинамики, но также для покрытия проблемной области, связанной с долговременными адаптационными
изменениями ССС под воздействием сопряженных систем организма. Поэтому,модель построена для учета влияния на локальную гемодинамику максимального количества вазоактивных химических агентов. Все разнообразие
подобных агентов по своему действию может быть подразделено на два типа: 1.сосудорасширяющий (ν) и 2. сосудосуживающий (ω). Каждый агент способен вызвать локальное изменение тонуса сосуда пропорционально своей
концентрации (С) и чувствительности (η) сосуда к агенту. Полагая аддитивность конечных эффектов, интегральные изменения тонуса сосудов,разложенного в нашей модели на два компонента - Di(t) и Ui(t), можно записать в следующей форме:

Заметим, что в формулах (14) и (15) СN и СA входят как составные
сосудосуживающие агенты.
Таким образом, система уравнений (1) – (15) представляет собой базовую
модель системного и легочного кровообращения в гемодинамически замкнутой,
физиологически автономной ССС с параллельными контурами
нейрогуморальной саморегуляции. Добавляя к ним условие (16), описывающее
открытость ССС для обмена плазмой крови между внутри- и внесосудистыми
пространствами как:
Воздействия внешних по отношению к ССС факторов на характеристики сердца, сосудов и регуляторных структур. При стабильных значениях констант модели будет иметь место стационарная осцилляция давлений, кровотоков и объемов крови во всех выделенных участках ССС в соответствии с заданной динамикой Di(t). Уровни перечисленных переменных состояния ССС в модели определяются набором ее констант и Vs. Задав произвольный закон изменений любого из перечисленных параметров или их комбинаций, можно имитировать динамические возмущения и отслеживать реакции модели на используемые входные нагрузки. Наиболее затребованными в прикладных исследованиях являются такие входные нагрузки, которые отражают эффекты изменения внешних физических воздействий (перемена позы, ускорения, микрогравитация, локальное или глобальное барометрическое давление, температура), физиологических сдвигов (мышечная деятельность, изменения активности различных органов или регуляторных структур и др.), а также эмоционального состояния. Именно поэтому, эти три группы воздействий включены в нашу модель в виде формируемых пользователем их комбинаций на заданном интервале моделирования.