Поэтому математические модели в прикладных отраслях должны строиться не только с точки зрения наиболее адекватного отражения сущности моделируемых процессов и явлений, но и с учетом особенностей мышления человека, его конкретных целей (несколько иные требования предъявляются к моделям, используемым в системах автоматического управления, однако проблемы автоматизации в данной книге не рассматриваются).
Поскольку принятие решения всегда направлено на разрешение некоторых проблем, процесс моделирования можно укрупненно представить в виде следующей последовательности действий:

• осознание наличия проблемы;
• выделение главных факторов, определяющих проблему, которые должны служить
выходными параметрами модели;
• выделение определяющих входных переменных модели;
• собственно разработка математической модели;
• идентификация модели (параметрическая или структурно-параметрическая);
• проведение численных экспериментов с моделью и при необходимости статистическая обработка полученных данных;
• определение состава параметров качества, характеризующих решаемую проблему (с использованием данных моделирования и априорной информации);
• формализация частных критериев качества на основе параметров качества;
• определение параметров, характеризующих относительную значимость частных критериев для решения общей проблемы;
• формализация обобщенного критерия качества решения проблемы на основе агрегирования частных критериев с учетом их относительной значимости;
• решение задачи выбора наилучшей альтернативы или многокритериальной оптимизации в зависимости от типа решаемой проблемы.

Следует подчеркнуть, что во многих реальных случаях решение проблем не требует построения конструктивной математической модели, адекватно описывающей все стороны исследуемого процесса или явления. Так, решение проблем принятия решений может сводиться к этапам анализа априорной информации и данных, полученных от экспертов, определения состава показателей качества и выбора наилучшей альтернативы из возможных. В этом случае также строятся модели, при этом они формализуют только указанные этапы и их можно условно называть моделями оптимизации или принятия решений. Отметим, что такие модели зачастую оказываются весьма сложными и требуют использования глубоких, современных математических методов для своей реализации.

Для иллюстрации рассмотрим следующий, на первый взгляд, простейший бытовой пример. Одному из авторов книги привелось пару месяцев читать лекции в одном иностранном государстве. Работа занимала большую часть дня, и это обстоятельство послужило причиной того, что меню этого автора состояло в основном из цыплят, запеченных в гриле (весьма дешевых и, что наиболее важно, обеспечивающих и обед, и ужин). Поскольку бытие все же в какой-то мере определяет сознание, автора заинтересовала проблема оптимизации приготовления цыплят. Основным фактором, почти целиком определяющим успех всего предприятия, оказалось время приготовления τ. От этого параметра качества напрямую зависели три основных частных критерия: вкус цыпленка μ _t( τ) , затраты электроэнергии на приготовление и время ожидания клиента в очереди μ _q( τ) . Проблемой является выбор оптимального по совокупности частных критериев времени приготовления.

Для умозрительной формализации частных критериев были применены функции желательности Харрингтона, широко применяемые в планировании экспериментов при поиске оптимальных условий [3]. Функции желательности изменяются от 0 в областях недопустимых (нежелательных) значений показателя качества до максимального значения, равного 1, в областях наиболее предпочтительных его значений. Других ограничений, кроме непрерывности и выпуклости, на функции желательности не налагается.

Из этих предпосылок экономический критерий затрат на энергию можно охарактеризовать функцией желательности μ _e( τ) , приведенной на рисунке 1. В соответствии с ней при τ <τ ₁ затраты энергии представляются для фирмы несущественным. С дальнейшим ростом растут затраты энергии, что отражается в уменьшении значений функции желательности до 0 при τ = τ ₈ При τ>τ ₈ производство становится нерентабельным ввиду слишком больших затрат на энергию. Поведение функции желательности, формализующей критерий ожидания клиента в очереди μ _q(τ), соответствует тому, что при τ<τ ₂ практически все клиенты готовы подождать приготовления пищи. С дальнейшим ростом τ все больше клиентов покидает очередь, поскольку хватает конкурирующих фирм, и при τ> τ ₅ клиенты считают время ожидания недопустимым.

Форма функции желательности критерия вкуса цыпленка μ _t определяется следующими соображениями. При τ< τ ₃ цыпленок будет сыроват. С ростом его вкусовые качества растут, и в интервале τ ₄ < τ < τ ₆ цыплята наиболее вкусны с точки зрения большинства клиентов. При τ > τ ₆ цыплята уже несколько суховаты, хотя находится достаточное число любителей именно поджаристых цыплят. При τ > τ ₇ цыплята становятся подгоревшими, и не находят покупателей.

Полученные на основе вышеприведенных умозрительных соображений функции желательности обладают существенно различными чертами. В принципе, критерий μ_e(τ) можно построить на основе объективных данных финансового анализа. Критерий μ_q(τ) - можно сконструировать на основе некоторых статистических данных. В отличие от них критерий μ_t(τ) основан, в основном, на субъективных оценках вкуса и вида поджаренных цыплят. Причем, в рассматриваемой ситуации именно субъективный критерий "вкус продукта" играет определяющую роль в успехе торгового предприятия. Исключение этого критерия из рассмотрения из-за его "субъективности" в данном случае сделало бы постановку задачи оптимизации работы пищевого предприятия практически бессмысленной.

Другим источником субъективизма при оценке работы предприятия является наличие нескольких частных критериев, являющихся антагонистичными. Улучшение с точки зрения критерия μ_t(τ) сопровождается одновременным ухудшением относительно критериев μ_e(τ) и μ_q(τ) (рис.1). Эта ситуация, как правило, имеет характер общей закономерности. Как указывается в [22], наличие в постановке задачи оптимизации хотя бы двух частных критериев неизбежно сопровождается привнесением в нее неопределенностей несогласованной, субъективной природы.

Следующими источниками субъективной неопределенности в рассматриваемом примере являются необходимость количественной оценки коэффициентов относительной важности частных критериев (ранжировка), а также выбор способа их агрегирования в обобщенный критерий качества.

Заканчивая рассмотрение нашего примера, отметим, что вес цыпленка является, вообще говоря, случайной переменной с соответствующим частотным распределением. Ясно, что время приготовления цыпленка должно зависеть от его веса, что делает необходимым одновременный учет в постановке задачи как субъективной, так и объективной (в данном случае статистической) неопределенностей. В итоге рассмотренная простейшая, на первый взгляд, бытовая проблема оказывается весьма сложной для разрешения с помощью формальных математических подходов.

Рассмотренный пример хорошо иллюстрирует основные особенности постановки задач оптимизации при разрешении реальных проблем: многокритериальность; антагонистичность и неравнозначимость частных критериев; важность учета критериев, основанных на субъективных оценках; необходимость одновременного учета неопределенностей различной природы. Во многих случаях дополнительной сложностью является иерархичность системы частных критериев.

В этом модельном примере также видны комплексность и многоаспектность проблем моделирования и оптимизации при постановке и решении реальных задач. Эта ситуация носит общий характер. Решение проблем оптимизации производственной деятельности непосредственно связано с моделированием и анализом технологических процессов, экономических показателей эффективности, а также с учетом техногенного воздействия промышленных производств на экологию окружающей среды. 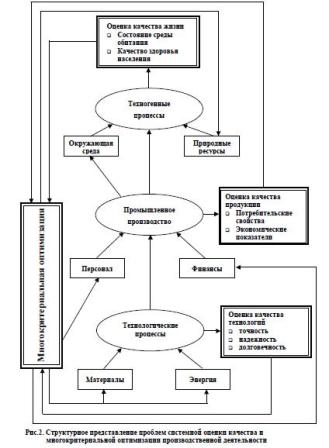Экологические факторы напрямую влияют на здоровье населения, а вся совокупность комплексных показателей деятельности на качество жизни в целом. Эту систему взаимозависимых производственно- технологических, экономических и экологических факторов можно наглядно представить укрупненной структурной схемой, приведенной на рисунке 2. Она отражает взаимосвязь задач и проблем, рассматриваемых в настоящей книге.

В первой главе приведены основные положения теории нечетких множеств, теории возможностей, прикладного интервального анализа в объеме, необходимом для понимания постановок задач, рассмотренных в последующих главах. Рассмотрены важные методологические проблемы взаимосвязи и разграничения нечеткости, возможности и вероятности. Показана глубокая взаимосвязь интервальной и нечетко-интервальной математики. Впервые во всей полноте представлена оригинальная, основанная на теоретико- вероятностном подходе, методика сравнения четких и нечетких интервалов (чисел), в дальнейшем широко используемая в задачах моделирования и оптимизации в условиях неопределенности. Даны краткие характеристики ряда других современных методов оперирования с неопределенностями, которые представляются весьма перспективными для практического использования.

Вторая глава посвящена проблемам многокритериальности. Рассмотрены методы формализации частных критериев с помощью функций принадлежности нечетким множествам, в том числе зависящих от интервальных и нечетко-интервальных аргументов. Введено новое, важное в практических приложениях понятие гипернечеткого множества, предложены процедуры построения частных критериев качества на основе гипернечетких функций принадлежности.

Описана методика ранжировки частных критериев на основе лингвистических матриц их парных сравнений, а также расширение методики для случая нечетко-интервальных матриц парных сравнений. Проанализирована проблема агрегирования частных критериев, описаны достоинства и недостатки различных вариантов построения обобщенного критерия качества. Предложена методика агрегирования иерархических систем частных критериев. Описана обобщенная постановка задач нечеткой многокритериальной оптимизации. Особое внимание уделено важным для практики проблемам многоэкстремальности и устойчивости оптимума.

В третьей главе рассмотрены проблемы моделирования и оптимизации технологических процессов. В начале главы изложены методологические принципы построения и редукции адекватных детерминированных математических моделей технологических процессов, ориентированных на использование в задачах оптимизации. Рассмотрена обобщенная постановка задачи структурно-параметрической идентификации детерминированных моделей, описана методика решения этой задачи, представленной в форме задачи многокритериальной оптимизации по совокупности критериев точности и физической достоверности модели.

Далее приведены конкретные примеры использования разработанных методик для совершенствования технологических процессов в металлургии. Рассмотрены задачи моделирования и многокритериальной оптимизации нагрева слитков под прокатку, термообработки стального проката, задача структурно-параметрической идентификации моделей процесса горячей прокатки алюминиевых сплавов и задача многокритериальной оптимизации этого процесса методом нечеткого динамического программирования.

Четвертая глава посвящена проблеме моделирования и оптимизации режимов работ энергоагрегатов в условиях неопределенности. Описана базовая методика нечеткой оптимизации на примере параллельной работы двух энергоагрегатов, использующих комбинированное топливо (газ и жидкое топливо). Поставлена общая задача нечеткой оптимизации работы совокупности энергоагрегатов, использующих комбинированное топливо в условиях неопределенности. Рассмотрены вопросы математической формализации технико- экономических критериев оптимизации работы энергоагрегатов. Подробно описана математическая модель совместного функционирования энергоагрегатов, приведены постановка и результаты решения задачи нечеткой оптимизации совместной работы энергоагрегатов ТЭЦ.

В пятой главе описаны методологические проблемы и результаты применения интервального анализа и нечетко-интервальной математики в имитационном моделировании производственных систем. Приведен пример многокритериальной нечетко-интервальной оптимизации на основе нечетко-интервальной имитационной модели (оптимизация обеспечения предприятия сырьем из нескольких источников). Рассмотрен пример нечетко- интервального имитационного моделирования процесса производства строительных материалов.

Шестая глава посвящена вопросам многокритериальной оценки техногенных последствий производственной деятельности, анализа влияния её на загрязнение окружающей среды и состояние здоровья населения. Представлена методика оценки и многокритериальной оптимизации качества воздушной среды в областном центре при учете ее влияния на состояние здоровья населения и наличии ограничений финансового характера.

В седьмой главе рассмотрены проблемы математического моделирования, многокритериальной оценки и оптимизации технико-экономических систем при наличии антагонистических критериев. С использованием конкретных примеров рассмотрены задачи многокритериальной и многоуровневой оценки качества коммерческих контрактов, а также качества промышленной продукции в условиях неопределенности. Представлены методика многокритериальной и многоуровневой оценки социально-экономического состояния регионов. Рассмотрены примеры математического моделирования и многокритериальной оптимизации финансовых параметров инвестиций в условиях нестатистической неопределенности.