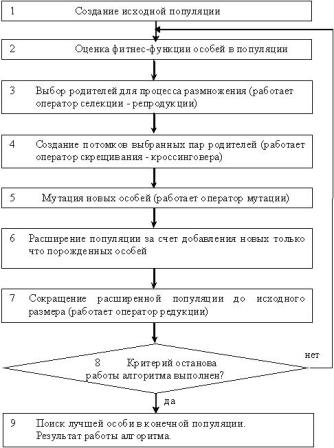
Рис.1.1. Простой генетический алгоритм
ГА используют принципы и терминологию, заимствованные у биологической науки - генетики. В ГА каждая особь представляет потенциальное решение некоторой проблемы. В классическом ГА особь кодируется строкой двоичных символов - хромосомой, каждый бит которой называется геном. Множество особей - потенциальных решений составляет популяцию. Поиск (суб)оптимального решения проблемы выполняется в процессе эволюции популяции - последовательного преобразования одного конечного множества решений в другое с помощью генетических операторов репродукции, кроссинговера и мутации.
ЭВ используют следующие механизмы естественной эволюции:
1) Первый принцип основан на концепции выживания сильнейших и естественного отбора по Дарвину, который был сформулирован им в 1859 году в книге "Происхождение видов путем естественного отбора". Согласно Дарвину особи, которые лучше способны решать задачи в своей среде, выживают и больше размножаются (репродуцируют). В генетических алгоритмах каждая особь представляет собой решение некоторой проблемы. По аналогии с этим принципом особи с лучшими значениями целевой (фитнесс) функции имеют большие шансы выжить и репродуцировать. Формализация этого принципа, как мы увидим далее, дает оператор репродукции.
2) Второй принцип обусловлен тем фактом, что хромосома потомка состоит из частей полученных из хромосом родителей. Этот принцип был открыт в 1865 году Менделем. Его формализация дает основу для оператора скрещивания (кроссинговера).
3) Третий принцип основан на концепции мутации, открытой в 1900 году де Вре. Первоначально этот термин использовался для описания существенных (резких) изменений свойств потомков и приобретение ими свойств, отсутствующих у родителей. По аналогии с этим принципом генетические алгоритмы используют подобный механизм для резкого изменения свойств потомков и тем самым, повышают разнообразие (изменчивость) особей в популяции (множестве решений).
Эти три принципа составляют ядро ЭВ. Используя их, популяция (множество решений данной проблемы) эволюционирует от поколения к поколению.
Эволюцию искусственной популяции - поиска множества решений некоторой проблемы формально можно описать алгоритмом, который представлен на рис.1.1.
ГА берет множество параметров оптимизационной проблемы и кодирует их последовательностями конечной длины в некотором конечном алфавите (в простейшем случае двоичный алфавит "0" и "1") .
Предварительно простой ГА случайным образом генерирует начальную популяцию стрингов (хромосом). Затем алгоритм генерирует следующее поколение (популяцию), с помощью трех основных генетических операторов:
1) Оператор репродукции (ОР);
2) Оператор скрещивания ( кроссинговера, ОК);
3) Оператор мутации (ОМ).
Генетические операторы являются математической формализацией приведенных выше трех основополагающих принципов Дарвина, Менделя и де Вре естественной эволюции.
ГА работает до тех пор, пока не будет выполнено заданное количество поколений (итераций) процесса эволюции или на некоторой генерации будет получено заданное качество или вследствие преждевременной сходимости при попадании в некоторый локальный оптимум.
В каждом поколении множество искусственных особей создается с использованием старых и добавлением новых с хорошими свойствами. Генетические алгоритмы - не просто случайный поиск, они эффективно используют информацию накопленную в процессе эволюции.
В процессе поиска решения необходимо соблюдать баланс между "эксплуатацией" полученных на текущий момент лучших решений и расширением пространства поиска. Различные методы поиска решают эту проблему по разному.
Например, градиентные методы практически основаны только на использовании лучших текущих решений, что повышает скорость сходимости с одной стороны, но порождает проблему локальных экстремумов с другой стороны. В полярном подходе случайные методы поиска используют все пространство поиска, но имеют низкую скорость сходимости. В ГА предпринята попытка объединить преимущества этих двух противоположных подходов. При этом операторы репродукции и кроссинговера делают поиск направленным. Широту поиска обеспечивает то что процесс ведется на множестве решений - популяции и используется оператор мутации.
В отличие от других методов оптимизации ГА оптимизируют различные области пространства решений одновременно и более приспособлены к нахождению новых областей с лучшими значениями целевой функции за счет объединения квазиоптимальных решений из разных популяций.
Каждый из функциональных блоков ГА рис.1.1, как показано в разделе 3(модификации и обобщения ГА), может быть реализован различными способами. Но сначала мы рассмотрим на простом примере основные моменты классического ГА.
1.2 Генетические операторыРассмотрим работу простого ГА на следующем примере. Надо найти (для простоты) целочисленное значение х в интервале от 0 до 31, при котором функции принимает максимальное значение.

Начальный этап работы ГА для данного примера приведен в верхней таблице (репродукция) рис.1.3.
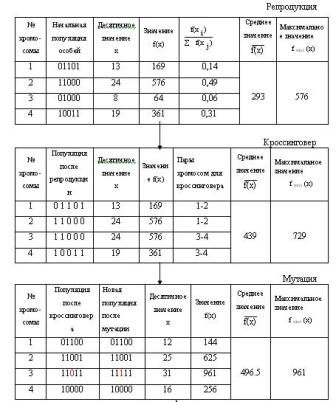
Здесь особи начальной популяции (двоичные коды значений переменных х - столбец 2) сгенерированы случайным образом. Двоичный код значения х называется хромосомой (она представляет генотип). Популяция образует множество потенциальных решений данной проблемы. В третьем столбце представлены их десятичные значения (фенотип). Далее на этом примере проиллюстрируем работу трех основных генетических операторов.
Репродукция - это процесс, в котором хромосомы копируются в промежуточную популяцию для дальнейшего "размножения" согласно их значениям целевой (фитнес-) функции. При этом хромосомы с лучшими значениями целевой функции имеют большую вероятность попадания одного или более потомков в следующее поколение.
Очевидно, оператор репродукции (ОР) является искусственной версией естественной селекции - выживания сильнейших по Дарвину. Этот оператор представляется в алгоритмической форме различными способами. Самый простой (и популярный) метод реализации ОР - построение колеса рулетки, в которой каждая хромосома имеет сектор, пропорциональный ее значению ЦФ. Для нашего примера "колесо рулетки" имеет следующий вид, представленный на рис.1.4.
Для селекции хромосом используется случайный поиск на основе колеса рулетки. При этом колесо рулетки вращается и после останова ее указатель определяет хромосому для селекции в промежуточную популяцию (родительский пул). Очевидно, что хромосома, которой соответствует больший сектор рулетки, имеет большую вероятность попасть в следующее поколение. В результате выполнения оператора репродукции формируется промежуточная популяция, хромосомы которой будут использованы для построения поколения с помощью операторов скрещивания.
В нашем примере выбираем хромосомы для промежуточной популяции, вращая колесо рулетки 4 раза, что соответствует мощности начальной популяции. Величину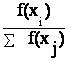 обозначим, как P(xi) , тогда ожидаемое количество копий i-ой хромосомы определяется M= P(xi)*N,
обозначим, как P(xi) , тогда ожидаемое количество копий i-ой хромосомы определяется M= P(xi)*N,
N-мощность популяции. Число копий хромосомы, переходящих в следующее поколение, иногда определяется и так:
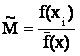
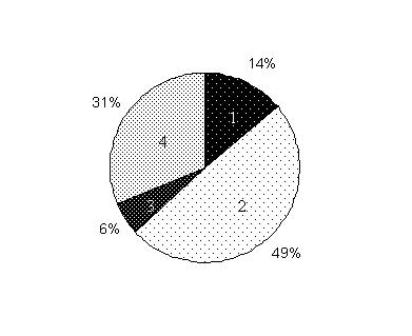
Расчетные числа копий хромосом по приведенной формуле следующие: хромосома 1 - 0,56; хромосома 2 - 1,97; хромосома 3 - 0,22; хромосома 4 - 1,23. В результате, в промежуточную популяцию 1-я хромосома попадает в одном экземпляре, 2-я - в двух, 3-я - совсем не попадает, 4-я - в одном экземпляре. Полученная промежуточная популяция является исходной для дальнейшего выполнения операторов кроссинговера и мутации.
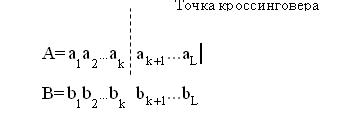
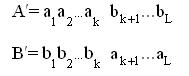
Следует отметить, что ОК выполняется с заданной вероятностью Pc (отобранные два родителя не обязательно производят потомков). Обычно величина Pc ≈0.5.
Таким образом, операторы репродукции и скрещивания очень просты - они выполняют копирование особей и частичный обмен частей хромосом. Продолжение нашего примера представлено на рис.1.3 во второй таблице (кроссинговер).
Сравнение с предыдущей таблицей показывает, что в промежуточной популяции после скрещивания улучшились все показатели популяции (среднее и максимальное значения ЦФ) .
Далее согласно схеме классического ГА с заданной вероятностью выполняется оператор мутации. Иногда этот оператор играет вторичную роль. Обычно вероятность мутации мала - Pc ≈0.001.
Оператор мутации (ОМ) выполняется в 2 этапа:
1-й этап. В хромосоме A=a1a2...aL случайно выбирается k-ая позиция (бит) мутации ( 1 ≤ k ≤ n ).
2-й этап. Производится инверсия значения гена в k-й позиции.![]()
Например, для хромосомы 11011 выбирается k=3 и после инверсии значения третьего бита получается новая хромосома - 11111. Продолжение нашего примера представлено в третьей таблице (мутация) рис.1.3. Таким образом, в результате применения генетических операторов найдено оптимальное решение x=31.
В данном случае, поскольку пример искусственно подобран, мы нашли оптимальное решение за одну итерацию. В общем случае ГА работает до тех пор, пока не будет достигнут критерий окончания процесса поиска и в последнем поколении определяется лучшая особь.
В данном случае, поскольку пример искусственно подобран, мы нашли оптимальное решение за одну итерацию. В общем случае ГА работает до тех пор, пока не будет достигнут критерий окончания процесса поиска и в последнем поколении определяется лучшая особь.