ДонНТУ Портал магистров ДонНТУ Библиотека

Библиотека





Achim Gegler Vortrag zum Seminar "Bildsegmentierung und Computer Vision"


Перевод Акульшиной Н.В.

Оригинал статьи расположен по адресу http://www.mathematik.uni-ulm.de/stochastik/lehre/ws05_06/seminar/gegler.pdf


1 Введение



На изображении необходимо определить сегмент изображения. Форма этого сегмента заранее известна априорной информацией. Необходимо найти: кривую, описывающую данный сегмент изображения. Кривая должна быть указана в явном виде. В этом контексте, так называемая кривая очертания или активный контур.

Цель: найти очертание, которое описывает сегмент изображения. Очертание систематизирует энергию.

Энергия = как подходят друг к другу априорная информация и очертание + как подходят друг к другу информация о изображении и очертание.

Чем меньше соответствие, тем выше энергия.

Задача: найти очертание с минимальной энергией, которое лучше всего охватывает сегмент.

Решение рассчитывается итеративно.




2 Определение


Определение кривой

Очертание описывает явное представление о параметрах кривой.

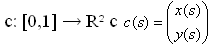
Требования: с 2 раза непрерывно дифференцировать.

Назначить энергию E(c)

R

E(c) = S(c) + P(c)

S(c) = внутренняя энергия (по априорной информации)

P(c) = (по информации с изображения)

Внутренняя энергия S(c)

Грубая форма как известно охватывает сегмент.

Мы знаем кое-что о "длине края" и "гладкости края" из этого сегмента.

Из дифференциальной геометрии:

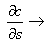
1. Производная кривой s говорит о длине.

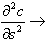
2. Производная кривой s говорит о гладкости.

c длина

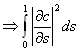
большая; c гладкость

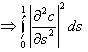
большая

Взвесив длину и кривизну: ω1≥0 и ω2≥0.

Выбираем ω1 и ω2 в соответствии с априорной информацией.

ω1>ω2: сегменты с сильной кривизной

ω1<ω2: очень гладкие сегменты

небольшая, когда очертание будет найдено хорошо известной формы сегмента.

Внешняя энергия P(c)

Изображение дано соответственно серого цвета из единичных пикселей.

Таким образом, функция (x,y) -> I(x,y)

I(x,y) = серый цвет на месте (x,y).

Исходя из I(x,y) непрерывно дифференцируема.

Сегменты изображения граничат по краям с окрестностями.

Край = месту, где появились большие изменения серого цвета.

Интересно: там, где

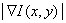
становится большим, насколько это возможно.

Энергия должна быть на краях маленькая.

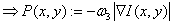
(ω3≥0 регулирующее воздействие внешней энергии в общей энергии)

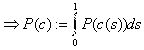
маленькое, когда очертание контура совпадает с краем изображения.



3 Определение решения


Статическая задача оптимизации

E(c) = S(c) + P(c)

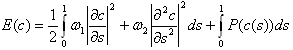
Задача оптимизации: E(c) -> min

-> необходимый критерий вариационного исчисления (уравнение Эйлера-Лагранжа)

Изменение задачи

Изменение задачи:

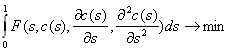
Необходимое условие для минимума:

(уравнение Эйлера-Лагранжа)

Обязательный критерий

Уравнение Эйлера-Лагранжа в нашем случае:

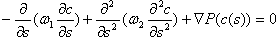
Итак, если мы приняли очертание с, мы можем решить, будет ли оно соответствовать (локальная) минимальная точка E(с).

Дискретизация

Очертание с описывается интерполяцией (например, с помощью конечных разностей). Если n<∞ узлов

сохраняются.

Производные

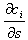
и

также численно рассчитаны в узлах.

Рассмотрим терм энергии:

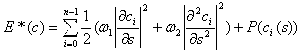
На изображение наложена сетка. Узлы должны находятся в узловых точках.

Итерационное вычисление

Инициализация очертания (указываем узлы), которые будут собраны за пределами сегмента.

Расчет энергии E*(C).

Единичный узел может сдвигать все 8 соседних точки сетки или оставить без изменений.

Для очертания есть в общей сложности 9n различных возможностей передвижения.

Выберите передвижение, для которого

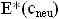
будет минимальным.



Преимущества и недостатки очертания

Преимущества

Рассмотрение априорной информации.

Существование эффективных процедур.

Надежность от шума на изображении и пробелов на кривой.

Недостатки

Не в состоянии справиться с топологическим изменениями -> T-очертание.

Реализация больших размеров только при значительных усилиях.



Инициализация очертания близкого к контуру сегмента (локальный минимум) является необходимым.



Литература


Наверх