Библиотека
Повышение точности решения задач вычислительной томографии путем нелинейной фильтрации восстановленного изображения. А.Б.Колкер
аспирант Новосибирского государственного технического университета, научный руководитель: доктор физико-математических наук, профессор Ю.Е.Воскобойников
Проекционные данные, регистрируемые в реальных компьютерных томографических системах, носят случайных характер, обусловленный следующими важными факторами. Во-первых, используемое рентгеновское излучение имеет ярко выраженную квантовую структуру. Число квантов, испускаемых рентгеновскими источниками за фиксированный интервал времени, является случайной величиной, поэтому элемент случайности заложен в самой природе источника излучения. Во-вторых, проходя через исследуемый объект, кванты поглощаются веществом случайным образом. В целях снижения дозы облучения, целесообразно снижать мощность излучения, что неизбежно приводит к увеличению относительного уровня шума.
При решении задач вычислительной томографии возникает известная проблема (общая для всех методов решения некорректных задач), обусловленная противоречием между разрешающей способностью и устойчивостью алгоритмов восстановления – увеличение разрешающей способности (т.е. уменьшение систематической ошибки восстановления) вызывает увеличение уровня случайной ошибки восстановления и наоборот.
Для решения этой проблемы в работе [1] был предложен следующий подход: для восстановления изображения по проекционным данным использовать алгоритмы с малой величиной систематической ошибки, например, алгоритм [2], а затем выполнить фильтрацию восстановленного изображения. К сожалению, использование комбинированного алгоритма, представляющего собой последовательность процедур медианной фильтрации и интервального скользящего среднего, не позволяет в полной мере сохранять резкие перепады уровня изображения из-за совпадения спектров случайной ошибки восстановления и «контрастных элементов» восстанавливаемого изображения. Это приводит к искажению формы фронтов и контрастных объектов.
Поэтому для фильтрации контрастных изображений предлагается использовать модифицированный медианный фильтр с рекурсивным формированием апертуры [3,4]. Применение такого фильтра позволяет получить лучшую гладкость отфильтрованных данных, при этом сохраняя контрастные детали изображения.
В процессе вычислительного эксперимента проекционные данные фантома Шеппа-Логана (Shepp-Logan) (рис.4), посчитанные для 60 углов с 721 параллельными лучами в каждой проекции, искажались 5% шумом с равномерным распределением. Восстановление производилось алгоритмом свертки с 1/(z*z) [2]. Результат восстановления фантома по зашумленным данным показан на рис.5.
В качестве характеристики точности оценивались два параметра. Среднеквадратическое отклонение:
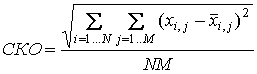
(1)
где: N - количество точек изображения по вертикали, M – количество точек изображения по горизонтали, xi,j - точки изображения после фильтрации,

- точки эталонного изображения;
и среднюю гладкость изображения Q:
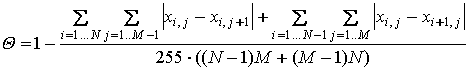
(2)
где: N - количество точек изображения по вертикали, M – количество точек изображения по горизонтали, xi,j - точки изображения.
Q=1 для полностью однородного изображения (все точки изображения имеют одинаковую яркость); Q=0, если в каждой точке происходит переход от минимального к максимальному разрешенному уровню яркости (“шахматная доска”).
Результат фильтрации восстановленного изображения предложенным алгоритмом показан на рис.6. Анализ его профиля (рис.1) показывает, что алгоритм позволяет хорошо удалять случайные шумы, при этом не вносит систематическую ошибку.
Сравнение СКО и Q изображений, отфильтрованных различными алгоритмами (рис.2, рис.3) показывает, что предложенный взвешенный медианный фильтр с рекурсивным формированием апертуры обеспечивает наилучшую гладкость и наименьшую среднеквадратическую ошибку из рассмотренных алгоритмов.
В заключении заметим, что предложенный алгоритм позволяет повысить точность решения томографических задач в целом.
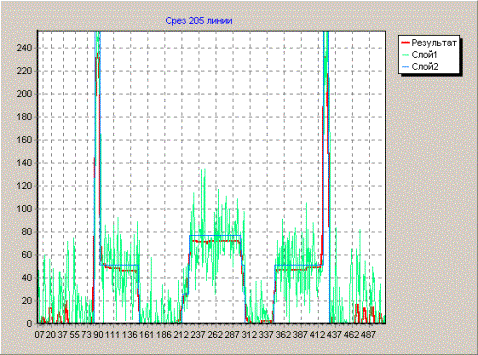
Рис.1. Профили изображений: слой1(зеленым) – восстановленные данные, слой2 (синим) – эталонные данные, результат (красным) данные, обработанные предложенным алгоритмом.
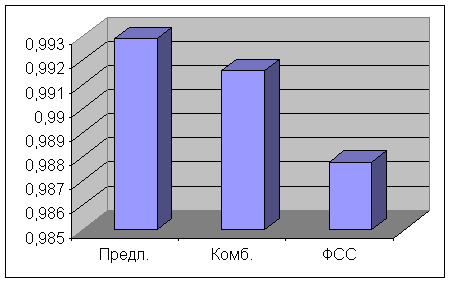
Рис.2. Гладкость Q результатов фильтрации различными алгоритмами (для исх. восстановленного изображения Q=0.9196 , для эталонного Q=0.9935 )
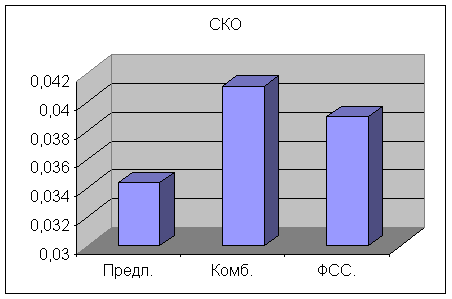
Рис.3. СКО результатов фильтрации различными алгоритмами (для исх. восстановленного изображения СКО=0,0623)
Литература.
- Воскобойников Ю.Е. Касьянова С.Н., Кисленко Н.П.,Трофимов О.Е. Использование алгоритмов нелинейной фильтрации для улучшения качества восстановленных томографических изображений.// Автометрия. 1997 №.3.
- Жирнов В.Т., Смирнов К.К., Трофимов О.Е. О численных методах решения задач томографии. В сб.: Методы и средства обработки изображений. Новосибирск: ИАиЭ СО АН СССР, 1982, С. 105-114.
- Воскобойников Ю.Е. Колкер А.Б. Адаптивный алгоритм фильтрации изображений и преобразования их в векторный формат.// Автометрия 2002, том 38,№4
- Колкер А.Б. Взвешенные и рекурсивные алгоритмы векторной медианной фильтрации. Сборник научных трудов НГТУ. Новосибирск: Изд-во НГТУ ,2000- Вып.5(22)
Наверх