Источник: "http://www.autex.spb.ru/download/dsp/dspa/dspa2003/tom2_64.pdf"
Для идентификации и классификации сложных биологических объектов наиболее высокоинформативным инвариантом является текстура. Примерами таких объектов могут быть радужная оболочка глаза и ядра белых кровяных телец.
Для описания текстуры используются три принципиальных подхода: структурный, спектральный и статистический. Исследования на примере ядер белых кровяных телец показали наибольшую эффективность классификации при использовании статистических текстурных описателей на основе модифицированных матриц совместной встречаемости уровней яркости. Положим размер анализируемого изображения Nx на Ny, число уровней яркости - Ng. Пусть Lx = {1,2...Nx} и Ly = {1,2...Ny} - соответственно горизонтальная и вертикальная пространственная область, a G = {1,2,...Ng}- множество уровней яркости изображения. Тогда изображение может быть определено следующим образом: I:Lx x Lv --> G. Матрица совместной встречаемости уровней яркости представляет собой оценку плотности распределения вероятностей второго порядка. Элемент матрицы представляет собой условную вероятность Р (i| j) возникновения уровня яркости i на расстоянии d от уровня яркости j.
Поскольку число таких матриц может быть очень большим, необходимы некоторые упрощения. Имеет смысл высчитывать 4 матрицы для заданного шага d для 0, 45, 90 и 135 градусов расположения пар уровней яркости.
Формально элементы матриц для указанных направлений могут быть записаны:
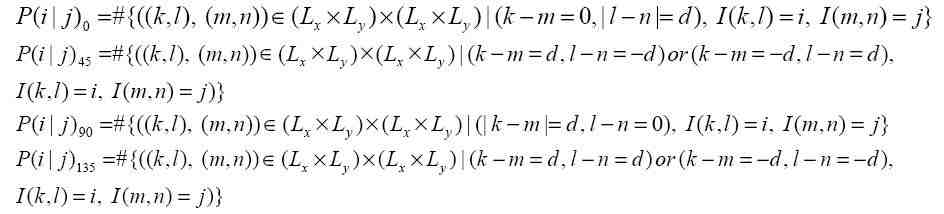
Полученные матрицы являются квадратными с размером pавным Ng. Для уменьшения вычислительных объемов изображение предварительно подвергается процедуре уменьшения уровней яркости. Для этой цели автором использовалась равновероятностная квантизация, и число рабочих уровней составило 3.
При применении шага для построения матриц > 1 большую информативность статистических описателей можно достигнуть, несколько модифицировав приведенный алгоритм. Предлагается рассчитывать вероятность P(i|j) возникновения уровня яркости i после последовательности размером d уровней яркости j. При этом матрицы совместной встречаемости становятся несимметричными (в отличие от классического подхода), что позволило ввести новые текстурные описатели, например треугольную симметрию. В ходе практического исследования выяснилось, что такой подход значительно улучшает разделяющую способность ряда статистических описателей при работе с низкочастотными текстурами:
Статистические текстурные описатели строятся на основании полученных матриц совместной встречаемости. 14 ставших уже классических текстурных описателя впервые упомянуты в [1]. К ним 7 параметров были добавлены в [2]. Для примера рассмотрим 3 из них:
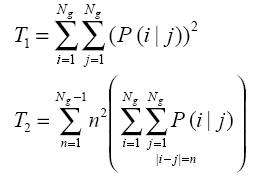
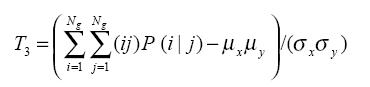
где 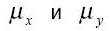 - математические ожидания частных распределений связанных c P(i|j) no
строкам и столбцам матриц соответственно, а
- математические ожидания частных распределений связанных c P(i|j) no
строкам и столбцам матриц соответственно, а 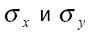 - соответствующие стандартные отклонения.
- соответствующие стандартные отклонения.
Выражение (T1) описывает угловой второй момент, являющийся мерой однородности текстуры. Формула (T2) определяет контраст изображения. Контраст является дифференциальным моментом матрицы совместной встречаемости и дает количественную оценку локальных изменений яркости, присутствующих на изображении. Параметр, заданный по (T3) - это корреляция, являющаяся мерой присутствия полутоновой линейной зависимости на изображении.
Каждый текстурный описатель вычисляется четыре раза - по числу сформированных матриц совместной встречаемости (для 0, 45, 90 и 135 градусов). Чаще всего приходится проводить инвариантный по вращению анализ объектов. В этом случае могут быть использованы статистические величины, полученные на основании четырех ориентированных значений: минимум, максимум, математическое ожидание, стандартное отклонение и другие.
Самая сложная и ответственная задача - построение минимального множества наиболее информативных высоко коррелированных параметров. Размер и состав этого множество сильно зависит от конкретной задачи распознавания (класса обрабатываемых объектов), а также выбранного шага для построения матриц. Грамотно построенное множество значительно увеличивает вероятность корректной классификации, а также позволяет уменьшить вычислительные ресурсы, требующиеся при построении, обучении и работе классификатора.
Литература
1. Haralick R. M. et al. Textural features for image classification// IEEE Transactions on Systems. Man and Cybernetics. 1973. pp. 610-621.
2. Pressman N. J. Markovian analysis of cervical cell images// The journal of histochemistry and cytochemistry. 1976. pp. 138-144.