En électronique, nous utilisons une grande variété de signaux analogiques ou numérique dont le support est, le plus souvent , une tension.

Ce support peut aussi être une onde électromagnétique (radio, TV, radar), une onde lumineuse ou infrarouge (fibres optiques) ou une onde sonore

L’information transportée est :

• un message audio (parole, musique)
• un message vidéo (image TV)
• un message binaire (liaison ordinateur-imprimante)
• un signal analogique traduisant l’état d’un capteur


Une façon naturelle de connaître un signal est d’observer son allure en fonction du temps : c’est la représentation temporelle, donnée par un oscillogramme.
Les exemples d’oscillogramme ci-dessous nous permettent de mettre en évidence plusieurs types de signaux :



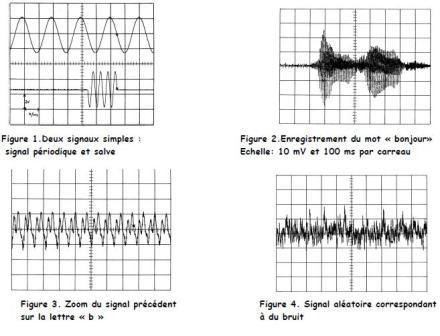
On peut donc classer les signaux en 4 catégories :

• les signaux périodiques (issus d’un GBF par exemple)
• les signaux non périodiques déterministes (impulsion, salve)
• les signaux pseudo-aléatoires (signal audio-vidéo)
• les signaux aléatoires (bruit électrique)

Les oscillogrammes nous renseignent sur l’amplitude, la valeur crête, la valeur moyenne, etc… mais pas sur les fréquences contenues dans le signal.

2) La représentation fréquentielle d’un signal simple

Le signal le plus simple du point de vue fréquence est le signal sinusoïdal.
Par exemple, x(t) = Esin(ωt) ne contient qu’une seule fréquence : f = ω/ 2π

Un signal parlé ou musical est plus complexe, puisque son allure varie constamment au cours du temps. Il contient des fréquences graves, moyennes et aiguës. Son spectre s’étend de 20 Hz à 20 kHz et varie en permanence entre ces deux fréquences extrêmes.
Le signal vidéo est encore plus complexe et son spectre s’étend du continu à quelques mégahertz.
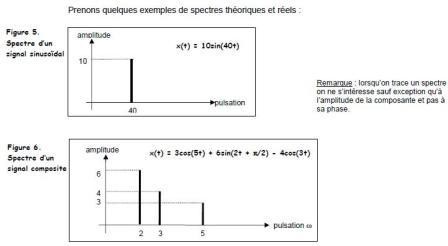
Le spectre d’un signal nous renseigne donc sur les différentes composantes fréquentielles qu’il contient.

Le spectre d’un signal est la représentation en fonction de la fréquence des amplitudes des différentes composantes présentes dans le signal.
Prenons quelques exemples de spectres théoriques et réels :




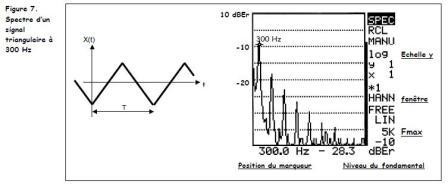
C’est un spectre forme de raies d’amplitudes decroissantes aux frequences f, 3f, 5f …

-up-