The Ant System: Optimization by a colony of cooperating agents
Marco Dorigo, Member, IEEE,Vittorio Maniezzo
and Alberto Colorni
Èñòî÷íèê: ftp://iridia.ulb.ac.be/pub/mdorigo/journals/IJ.10-SMC96.pdf
Introduction
In this paper we define a
new general-purpose heuristic algorithm which can be used to solve different
combinatorial optimization problems. The new heuristic has the following
desirable characteristics:
· It is versatile, in
that it can be applied to similar versions of the same problem; for example,
there is a straightforward extension from the traveling salesman problem (TSP)
to the asymmetric traveling salesman problem (ATSP).
· It is robust. It can be
applied with only minimal changes to other combinatorial optimization problems
such as the quadratic assignment problem (QAP) and the job-shop scheduling
problem (JSP).
· It's population based
approach. This is interesting because it allows the exploitation of positive
feedback as a search mechanism, as explained later in the paper. It also makes
the system amenable to parallel implementations (though this is not considered
in this paper).
These desirable properties
are counterbalanced by the fact that, for some applications, the Ant System can
be outperformed by more specialized algorithms. This is a problem shared by
other popular approaches like simulated annealing (SA), and tabu search (TS),
with which we compare the Ant System. Nevertheless, we believe that, as is the
case with SA and TS, our approach is meaningful in view of applications to
problems which, although very similar to well known and studied basic problems,
present peculiarities which make the application of the standard
best-performing algorithm impossible. This is the case, for example, with the
ATSP.
In the approach discussed
in this paper we distribute the search activities over so-called
"ants," that is, agents with very simple basic capabilities which, to
some extent, mimic the behavior of real ants. In fact, research on the behavior
of real ants has greatly inspired our work (see [10], [11], [21]). One of the
problems studied by ethologists was to understand how almost blind animals like
ants could manage to establish shortest route paths from their colony to
feeding sources and back. It was found that the medium used to communicate
information among individuals regarding paths, and used to decide where to go,
consists of pheromone trails. A moving ant lays some pheromone (in varying quantities)
on the ground, thus marking the path by a trail of this substance. While an
isolated ant moves essentially at random, an ant encountering a previously laid
trail can detect it and decide with high probability to follow it, thus
reinforcing the trail with its own pheromone. The collective behavior that
emerges is a form of autocatalyticbehavior1 where the more the ants following a
trail, the more attractive that trail becomes for being followed. The process
is thus characterized by a positive feedback loop, where the probability with
which an ant chooses a path increases with the number of ants that previously
chose the same path.
Consider for example the
experimental setting shown in Fig. 1. There is a path along which ants are
walking (for example from food source A to the nest E, and vice versa, see Fig.
1a). Suddenly an obstacle appears and the path is cut off. So at position B the
ants walking from A to E (or at position D those walking in the opposite
direction) have to decide whether to turn right or left (Fig. 1b). The choice
is influenced by the intensity of the pheromone trails left by preceding ants.
A higher level of pheromone on the right path gives an ant a stronger stimulus
and thus a higher probability to turn right. The first ant reaching point B (or
D) has the same probability to turn right or left (as there was no previous
pheromone on the two alternative paths). Because path BCD is shorter than BHD,
the first ant following it will reach D before the first ant following path BHD
(Fig. 1c). The result is that an ant returning from E to D will find a stronger
trail on path DCB, caused by the half of all the ants that by chance decided to
approach the obstacle via DCBA and by the already arrived ones coming via BCD:
they will therefore prefer (in probability) path DCB to path DHB. As a
consequence, the number of ants following path BCD per unit of time will be
higher than the number of ants following BHD. This causes the quantity of
pheromone on the shorter path to grow faster than on the longer one, and
therefore the probability with which any single ant chooses the path to follow
is quickly biased towards the shorter one. The final result is that very
quickly all ants will choose the shorter path.
The algorithms that we are
going to define in the next sections are models derived from the study of real
ant colonies. Therefore we call our system Ant System(AS) and the algorithms we
introduce ant algorithms. As we are not interested in simulation of ant
colonies, but in the use of artificial ant colonies as an optimization tool,
our system will have some major differences with a real (natural) one:
· artificial ants will have some memory,
· they will not be completely blind,
· they will live in an environment where
time is discrete.
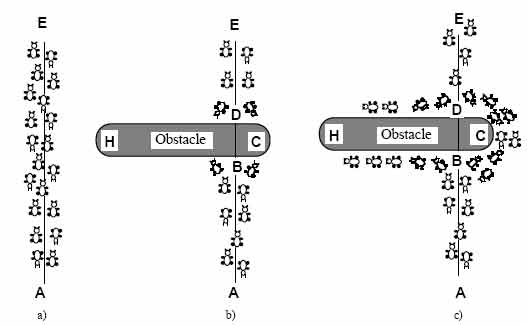
Fig. 1. An example with real ants.
a) Ants follow a path between points A and E.
b) An obstacle is interposed; ants can choose to go around it following one of
the two different paths with equal probability.
c) On the shorter path more pheromone is laid down.
Nevertheless, we believe
that the ant colony metaphor can be useful to explain our model. Consider the
graph of Fig. 2a, which is a possible AS interpretation of the situation of
Fig. 1b. To fix the ideas, suppose that the distances between D and H, between
B and H, and between B and D-via C-are equal to 1, and let C be positioned half
the way between D and B (see Fig. 2a). Now let us consider what happens at
regular discretized intervals of time: t=0, 1, 2
Suppose that 30 new ants
come to B from A, and 30 to D from E at each time unit, that each ant walks at
a speed of 1 per time unit, and that while walking an ant lays down at time t a
pheromone trail of intensity 1, which, to make the example simpler, evaporates
completely and instantaneously in the middle of the successive time interval
(t+1, t+2). At t=0 there is no trail yet, but 30 ants are in B and
This
process continues until all of the ants will eventually choose the shortest
path.
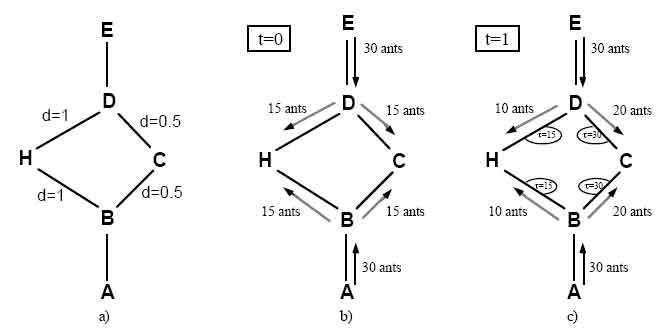
Fig. 2. An example with artificial ants.
a) The initial graph with distances.
b) At time t=0 there is no trail on the graph edges; therefore, ants choose
whether to turn right or left with equal probability.
c) At time t=1 trail is stronger on shorter edges, which are therefore, in the
average, preferred by ants.
The idea is that if at a given point an ant has to choose among different paths, those which were heavily chosen by preceding ants (that is, those with a high trail level) are chosen with higher probability. Furthermore high trail levels are synonymous with short paths.
The Ant System
In this section we introduce the AS. We decided to use the well-known traveling salesman problem [26] as benchmark, in order to make the comparison with other heuristic approaches easier [20]. Although the model definition is influenced by the problem structure, we will show in Section VII that the same approach can be used to solve other optimization problems.
Given a set of n towns, the
TSP can be stated as the problem of finding a minimal length closed tour that
visits each town once. We call dij the length of the path between towns i and
j; in the case of Euclidean TSP, dij is the Euclidean distance between i and j
(i.e., 
).
An instance of the TSP is given by a graph (N,E), where N is the set of towns
and E is the set of edges between towns (a fully connected graph in the
Euclidean TSP).
Let 
be the number of ants in town i at
time t and let m 
be
the total number of ants. Each ant is a simple agent with the following
characteristics:
· it chooses the town to go to with a probability that is a function of the town distance and of the amount of trail present on the connecting edge;
· to force the ant to make legal tours, transitions to already visited towns are disallowed until a tour is completed (this is controlled by a tabu list);
· when it completes a tour, it lays a
substance called trail on each edge (i,j) visited. Let 
be the intensity of trail
on edge (i,j) at time t. Each ant at time t chooses the next town, where it
will be at time t+1. Therefore, if we call an iteration of the
AS algorithm the m moves carried out by the m ants in the interval (t, t+1),
then every n iterations of the algorithm (which we call a cycle) each ant has
completed a tour. At this point the trail intensity is updated according to the
following formula
(1)
where 
is a
coefficient such that (1 - ) represents the evaporationof trail between time t and t+n,
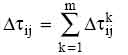(2)
where 
is
the quantity per unit of length of trail substance (pheromone in real ants)
laid on edge (i,j) by the k-th ant between time t and t+n; it is given by
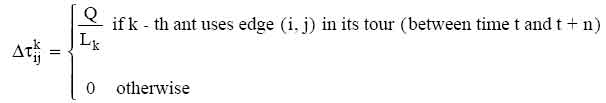(3)
where Q is a constant and Lk is the tour length of the k-th ant.
The coefficient must be set to a value < 1 to
avoid unlimited accumulation of trail (see note 1). In our experiments, we set
the intensity of trail at time , 
, to a small positive constant c.
In order to satisfy the constraint that an ant visits all the n different towns, we associate with each ant a data structure called the tabu list2, that saves the towns already visited up to time t and forbids the ant to visit them again before n iterations (a tour) have been completed. When a tour is completed, the tabu list is used to compute the ant's current solution (i.e., the distance of the path followed by the ant). The tabu list is then emptied and the ant is free again to choose. We define tabuk the dynamically growing vector which contains the tabu list of the k- th ant, tabuk the set obtained from the elements of tabuk , and tabuk (s) the s-th element of the list (i.e., the s-th town visited by the k-th ant in the current tour).
We call
visibility 
the
quantity 1/dij. This quantity is not modified during the run of the AS, as
opposed to the trail which instead changes according to the previous formula
(1). We define the transition probability from town i to town j for the k-th
ant as
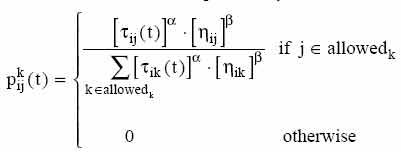
where allowedk = {N - tabuk} and where and are parameters that control the
relative importance of trail versus visibility. Therefore the transition
probability is a trade-off between visibility (which says that close towns
should be chosen with high probability, thus implementing a greedy constructive
heuristic) and trail intensity at time t (that says that if on edge (i,j) there
has been a lot of traffic then it is highly desirable, thus implementing the
autocatalytic process).
The algorithms
Given the definitions of the preceding section, the so-called ant-cyclealgorithm is simply stated as follows. At time zero an initialization phase takes place during which ants are positioned on different towns and initial values ij(0) for trail intensity are set on edges. The first element of each ant's tabu list is set to be equal to its starting town. Thereafter every ant moves from town i to town j choosing the town to move to with a probability that is a function (with parameters and see formula (4)) of two desirability measures. The first, the trail ij(t), gives information about how many ants in the past have chosen that same edge (i,j); the second, the visibility ij, says that the closer a town the more desirable it is. Obviously, setting = 0, the trail level is no longer considered, and a stochastic greedy algorithm with multiple starting points is obtained.
After n iterations all ants have completed a tour, and their tabu lists will be full; at this point for each ant k the value of Lk is computed and the values kj are updated according to formula (3). Also, the shortest path found by the ants (i.e., min Lk, k = 1, ..., m) is saved and all the tabu lists are emptied. This process is iterated until the k tour counter reaches the maximum (user-defined) number of cycles NCMAX , or all ants make the same tour. We call this last case because it denotes a situation in which the algorithm stops searching for alternative solutions.
Formally the ant-cyclealgorithm is:
1.Initialize: Set t:=0 {t is the time counter} Set NC:=0 {NC is the cycles counter}For every edge (i,j) set an initial value
2. Set s:=1 {s is the tabu list index} For k:=1 to m do Place the starting town of the k-th ant in tabuk(s) 3. Repeat until tabu list is full {this step will be repeated (n-1) times} Set s:=s+1 For k:=1 to m do Choose the town j to move to, with probability pkj (t ) given by equation (4) {at time t the k-th ant is on town i=tabuk (s-1)} Move the k-th ant to the town j Insert town j in tabuk (s) 4. For k:=1 to m do Move the k-th ant from tabuk (n) to tabuk (1) Compute the length Lk of the tour described by the k-th ant Update the shortest tour found For every edge (i,j)For k:=1 to m do
5. For every edge (i,j) compute ij(t+n) according to equation ij(t+n)= . ij(t)+ ij Set t:=t+n Set NC:=NC+1 For every edge (i,j) set ij:=0 6. If (NC < NCMAX) and (not stagnation behavior) then Empty all tabu lists Goto step 2 else Print shortest tour
Stop