Муравьиные системы: Оптимизация при помощи колонии взаимодействуюих агентов
Marco Dorigo,
Member, IEEE,Vittorio Maniezzo and Alberto Colorni
Источник: ftp://iridia.ulb.ac.be/pub/mdorigo/journals/IJ.10-SMC96.pdf
Автор перевода: Гливка А.Г.
Введение
В этой статье описан новый эвристический алгоритм общего назначения, который может быть использован для решения различных комбинаторно-оптимизационных проблем. Этот алгоритм имеет несколько превосходных характеристик.
· Многогранность - может применяться для похожих интерпретаций одной и той же проблемы. К примеру, может применяться для решения прямой (симметричной) задачи коммивояжера(TSP), так и для решения ассиметричной задачи(ATSP).
· Устойчивость - может применяться с минимальными изменениями для других комбинаторно-оптимизационных проблем, таких как квадратичная задача о назначениях (QAP) и задача календарного планирования (JSP).
· Близость к алгоритмам основанных на популяциях - позволяет использовать положительные обратные связи, как механизм поиска, что будет описано в дальнейшем. Также делает систему податливой для параллельного внедрения.
Впервые проблемой поведения муравьев заинтересовались этологи, которые хотели понять как почти слепые животные, такие как муравьи, могли находить кратчайший путь от их гнезда к пище и обратно. Было выяснено, что муравьи общаются посредством следов феромона, отложенного на путях, которыми они следуют. Муравей откладывает феромон на землю, образуя след. Отдельно взятый муравей двигается случайно, тогда как муравей, который наткнулся на первоначально отложенный след, с большой вероятностью решит следовать этим путем, таким образом, откладывая новый слой феромона. Появление такой формы коллективного поведения называется автокаталитическим поведением - чем больше муравьев идут по следу, тем больше муравьев выберут этот путь.
Рассмотрим пример, показанный на рис.1. Здесь изображен путь, по которому прогуливаются муравьи (например от источника пищи А к гнезду Е, и наоборот рис 1а). Внезапно препятствие появляется и преграждает путь. Таким образом, в месте В муравьи, идущие от А к Е (или в месте D от Е к А) должны решить повернуть направо или налево рис.1b. На выбор влияет интенсивность феромонового следа, оставленного предшествующими муравьями. Поэтому большее количество феромона справа, стимулирует муравьев поворачивать направо. Первый муравей, достигший точки B (или D) с равной вероятность может повернуть как направо, так и налево (т.к. на альтернативных путях еще нет феромона). В следствие того, что путь BCD короче чем BHD, первый муравей идущий этим путем достигнет точки D быстрее муравья, шедшего путем BHD (рис. 1c). Таким образом, муравей возвращающийся из Е в D найдет более сильным след на пути DCB, появившийся из-за того, что половина муравьев решила обойти препятствие путем DCBA и некоторые достигли цели через BCD: в дальнейшем вероятно они предпочтут путь DCB пути DHB. Как следствие, количество муравьев последовавших путем BCD за единицу времени будет больше, чем количество на пути BHD. Это приводит к тому, что отложение феромона на коротком пути происходит быстрее, чем на длинном и вероятность выбора короткого пути муравьем также возрастает. В результате вскоре все муравьи выбирают короткий путь.
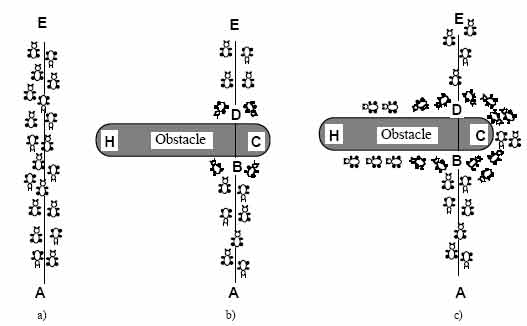
Рисунок
1 - Пример с
настоящими
муравьями
a) Муравьи
идут по пути
между
точками А и Е.
b) Появление
препятствия;
муравьи с
равной
вероятностью
выбирают
один из путей
обхода
препятствия
c) На коротком
пути
отложено
большее
количество
феромона
Тем не менее, мы полагаем, что пример с муравьями может быть полезен для объяснения нашей модели. Рассмотрим граф на рисунке 2а, который является возможной интерпретацией с помощью муравьиной системы ситуации на рисунке 1b.
Предположим, что расстояние между D и H, между B и H, и между B и D- через C-равны 1, и пусть C располагается на полпути между D и B (смотри рис 2a. Теперь рассмотрим, что будет проистходить в интервалы времени t=0, 1, 2.
Предполагается, что 30 новых муравьев идут в точку В из точки А, и 30 в D из E в каждый момент времени, который каждый муравей проходит со скоростью 1 за каждый момент времени. Пока муравей идет, он откладывает в момент времени t феромон с интенсивностью 1, и , чтобы сделать пример проще, испаряется полностью и мгновенно во временной интервал (t+1, t+2). В момент времени t=0 следа еще нет, но 30 муравьев в точке В и 30 в D. Их выбор каким путем пойти полностью случаен. Вследствие этого, в среднем 15 муравьев из каждого узла будут двигаться по направлению к H, и 15 по направлению к C (рис. 2b) В момент времени t=1 30 новых муравьев, которые шли в В из А обнаружат след с интенсивностью 15 на пути, который ведет к Н, оставленный 15 муравьями, которые шли этим путем из точки В, и след с интенсивностью 30 на пути С, полученный как сумма следа отложенного 15 муравьями которые шли из В и 15, которые пришли в В из D через С (рис. 2c)
Этот процесс
продолжается
пока все
муравьи случайным
образом
выберут
короткий
путь.
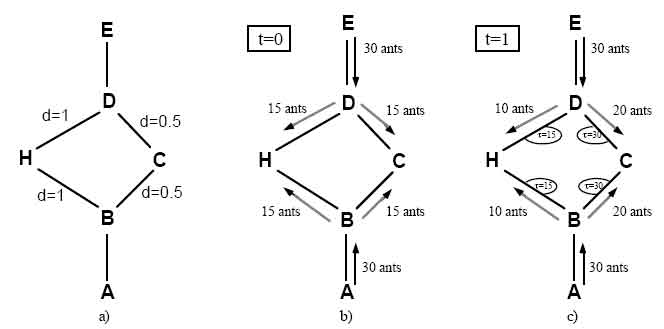
Рисунок
2 - Пример с
искусственными
муравьями
a) Начальный
граф с
расстояниями
b) В момент
времени t=0 нет
никакого
следа на ребрах
графа; далее
муравьи
выбирают
повернуть
налево или
направо с
равной
вероятностью
c) В момент
времени t=1
след сильнее
на коротком
ребре, потому
как он был
предпочтительней
для муравьев
Муравьиная система
В этой части представлена муравьиная система (AS). Было решено использовать известную задачу коммивояжера, чтобы сравнить с другими вероятностными методами.
Дано
множество из
n городов,
задача
коммивояжера
представляет
собой
проблему
нахождения
самого
короткого пути,
при условии,
что каждый
город был
посещен лишь
раз.
Обозначим dij -
длина пути
между городами
i и j; в случае
эвклидовой
задачи коммивояжера
dij - эвклидово
расстояние
между i и j; (т.е. ![]() ).
В данной
задаче дан
граф (N,E), где N
множество городов
и Е множество
граней между
городами is the
(полносвязный
граф в
эвклидовой
задаче коммивояжера).
).
В данной
задаче дан
граф (N,E), где N
множество городов
и Е множество
граней между
городами is the
(полносвязный
граф в
эвклидовой
задаче коммивояжера).
Пусть ![]() количеств
муравьев в
городе i в
момент времени
t
количеств
муравьев в
городе i в
момент времени
t ![]() - общее
количество
муравьев.
Kаждый
муравей это
простой
агент со
следующими
характеристиками:
- общее
количество
муравьев.
Kаждый
муравей это
простой
агент со
следующими
характеристиками:
· он выбирает город, в который следует с вероятностью, зависящей от удаленности города и количества следа феромона, отложенного на ребре;
· посещенные города становятся недоступными для повторного посещения, пока не закончен маршрут. (Это контролируется при помощи специального списка городов);
· как
только
маршрут
закончен,
агент откладывает
вещество,
называемое
следом на
каждом
посещенном
ребре (i,j). Пусть ![]() интенсивность
следа на
ребре (i,j) в
момент времени
t. Kаждый муравей
в момент
времени t
выбирает
следующий
город, в
котором он
будет в
момент
времени t+1.
таким
образом, если
мы назовем
итерацией m передвижений,
произведенных
m муравьями в интервале
времени (t, t+1),
тогда каждые
n итераций
алгоритма
(так
называемого цикла)
каждый
муравей
закончит
маршрут. Таким
образом,
интенсивность
следа
обновляется
по формуле
интенсивность
следа на
ребре (i,j) в
момент времени
t. Kаждый муравей
в момент
времени t
выбирает
следующий
город, в
котором он
будет в
момент
времени t+1.
таким
образом, если
мы назовем
итерацией m передвижений,
произведенных
m муравьями в интервале
времени (t, t+1),
тогда каждые
n итераций
алгоритма
(так
называемого цикла)
каждый
муравей
закончит
маршрут. Таким
образом,
интенсивность
следа
обновляется
по формуле
![]() (1)
(1)
Где ![]() это
коэффициент
такой, что (1 -
это
коэффициент
такой, что (1 - ![]() )
представляет
собой
испарение
следа между
временем t и t+n,
)
представляет
собой
испарение
следа между
временем t и t+n,
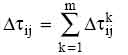 (2)
(2)
where ![]() is the
quantity per unit of length of trail substance (pheromone in real ants) laid on
количество
феромона
отложенного
на ребре (i,j) k-м
муравьем в
момент времени
t и t+n;
is the
quantity per unit of length of trail substance (pheromone in real ants) laid on
количество
феромона
отложенного
на ребре (i,j) k-м
муравьем в
момент времени
t и t+n;
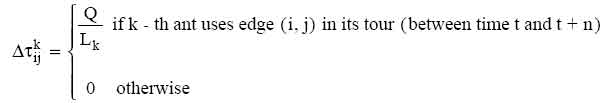 (3)
(3)
где Q
константа и Lk -
это длина
маршрута
к-ого муравья.
Коэффициент ![]() must
be set to a value < 1 to avoid unlimited accumulation of trail (see note 1).
должен быть
установлен в
значение <1
для
избегания
безграничного
отложения
следа. В
нашем эксперименте
мы
устанавливаем
интенсивность
отложения
следа в
момент 0,
must
be set to a value < 1 to avoid unlimited accumulation of trail (see note 1).
должен быть
установлен в
значение <1
для
избегания
безграничного
отложения
следа. В
нашем эксперименте
мы
устанавливаем
интенсивность
отложения
следа в
момент 0, ![]() ,
как малую
положительную
константу c.
,
как малую
положительную
константу c.
Чтобы было выполнено условие посещения муравьем n разных городов, к каждому муравью привязывается специальная структура данных, называемая tabu list2. Этот список содержит посещенные города к времени t и запрещает муравьям посещать их снова, пока не пройдено n итераций (т.е не был окончен маршрут). Когда маршрут закончен tabu list используется для определения решения, найденного данным муравьем (т.е расстояния пройденного муравьем), затем список опустошается и муравей может делать выбор снова. Пусть tabuk динамически растущий вектор, связанный со списком k-м муравьем, tabuk - множество полученное из элементов tabuk, и tabuk(s), s-й элемент списка (т.е s-й город, посещенный k-м муравьем в текущем маршруте).
Назовем
видимостью ![]() количество
1/dij. Это
количество
неизменно на протяжении
всего
алгоритма, в
отличие от следа,
который
изменяется в
соответствии
с формулой (1).
Вычислим
вероятность
перехода из
города i в
город j k-м
муравьем
количество
1/dij. Это
количество
неизменно на протяжении
всего
алгоритма, в
отличие от следа,
который
изменяется в
соответствии
с формулой (1).
Вычислим
вероятность
перехода из
города i в
город j k-м
муравьем
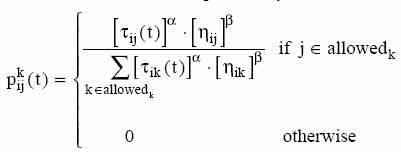
где allowedk = {N - tabuk},![]() и
и ![]() -
параметры, задающие
веса следа
феромона.
-
параметры, задающие
веса следа
феромона.
Алгоритм
1. Инициализация:Устанавливаем t:=0 {t счетчик времени}Устанавливаем NC:=0 {NC is the cycles counter}
Для каждого ребра (i,j) устанавливаем начальное значение ij(t)=c для интенсивности следа и ij= 0Размещаем m муравьев в n узлах 2. Set s:=1 {s - индекс tabu list}
For k:=1 to m doРазмещаем стартовый город k-го муравья в tabuk(s) 3. Repeat until tabu list заполнен {этот шаг будет повторяться (n-1) раз}Устанавливаем s:=s+1
For k:=1 to m do
Выбор города j для дальнейшего движения, с вероятностью pijk (t) по формуле (4){в момент времени t k-й муравей находится в городе i=tabuk(s-1)}Движение k-го муравья в город jДобавление города j в tabuk(s) 4. For k:=1 to m doПеремещаем k-го муравья из tabuk(n) в tabuk(1)Вычисляем длину маршрута Lk, проденного k-м муравьемОбновляем кратчайший найденный путь для каждого ребра (i,j)For k:=1 to m do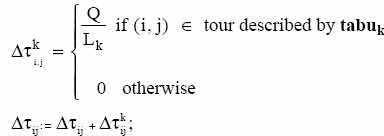
5. Для каждого ребра (i,j) вычисляется ij(t+n) в соответствии с формулой 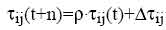
Устанавливаем t:=t+n Устанавливаем NC:=NC+1 Для каждого ребра (i,j) устанавливаем ij:=0 6. If (NC < NCMAX) and (not stagnation behavior)
Очищаем все tabu lists
Переход к шагу 2 else Печать самого короткого пути Stop