|
Чисто квадрупольный резонанс Э. Эндрю Ссылка на источник: Э. Эндрю. Ядерный магнитный резонанс/Пер. с англ. Н.М. Померанцева и Е.Н. Скубур. – М.: 1957. – 296 с. (с. 247-253) В п. 3 этой главы мы отметили, что для Аl203 возмущение ядерных магнитных энергетических уровней ядерным электрическим квадрупольным взаимодействием обусловливает существенную долю расщепления этих уровней, вызванного магнитным полем в несколько тысяч эрстед. Во многих твердых телах электрическое квадрупольное взаимодействие еще больше, обусловливая гораздо большее расщепление, чем то, которое происходит за счет магнитного поля не слишком большой напряженности. Это особенно справедливо для молекулярных твердых тел, где градиент электрического поля имеет внутримолекулярное происхождение и того же порядка величины, как в свободных молекулах. Для ковалентно связанных молекул типичные значения e^2Qq/h для С135, Вr79 и J127 равны 80, 500 и 2000 мггц соответственно. Очевидно, что в таких случаях квадрупольное взаимодействие несет основную ответственность за разрешение вырождения и что любое присутствующее магнитное поле должно рассматриваться как возмущение квадрупольного взаимодействия. Поэтому в таких твердых телах существует большое расщепление даже при отсутствии магнитного поля, что обусловливает возможность получения резонансного обмена радиочастотной энергии с твердым телом даже в отсутствие приложенного магнитного поля. Первый удачный эксперимент был проведен Демельтом и Крюгером, которые нашли резонансы для С135 и С137 (оба имеют спиновое число 3/2) в твердом транс-1,2-дихлор-этилене при частотах 35, 40 и 27,96 мггц соответственно. Это явление можно все же считать ядерным магнитным резонансом, поскольку, как мы увидим ниже, связь между ядром и высокочастотным электромагнитным полем, которая вызывает ядерные переходы, является магнитной. Тем не менее расщепление энергетических уровней имеет немагнитное, а электрическое происхождение, и по этой причине, чтобы подчеркнуть отсутствие приложенного магнитного поля, явление обычно называют ядерным квадрупольным резонансом, или чисто квадрупольным резонансом. Чисто квадрупольный резонанс стал теперь самостоятельным предметом изучения, и мы дадим здесь лишь краткое его описание; более детальное обсуждение вопроса можно найти в превосходном обзоре Демельта. Рассмотрим сначала с классической точки зрения ядро, обладающее электрическим квадрупольным моментом и находящееся в электронном окружении с осевой симметрией, причем ось симметрии направлена вдоль оси z. Пусть ось спина ядра, а следовательно, и вектор магнитного момента, наклонены к оси z под углом θ (фиг. 59). Тогда, как показал Демельт, классическая энергия квадрупольного взаимодействия равна
Так как Е является функцией θ, то на ядро должна действовать пара сил dE/dθ, стремящаяся повернуть ось ядра по направлению к оси z или от оси z в зависимости от знака Qq. Ядерный спин под действием пары сил прецессирует вокруг оси z. В результате появляются компоненты магнитного дипольного момента и электрического квадрупольного момента, вращающиеся вокруг оси z.
Фиг. 59. Схематическое изображение прецессии ядерного квадруполя вокруг оси симметрии его электронного окружения.
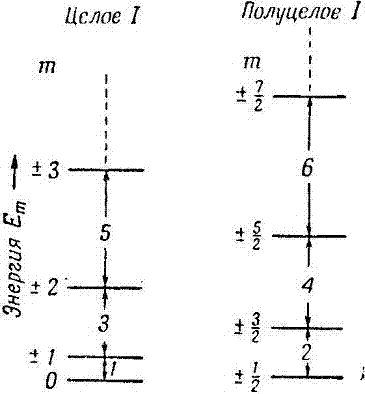
Фиг. 60. Энергетические уровни, возникающие за счет взаимодействия ядерного электрического квадруполя с аксиально симметричным электрическим полем.
Поэтому, если наложить высокочастотное поле с частотой, равной частоте прецессии, и с магнитным или электрическим вектором, вращающимся в том же направлении вокруг оси z, то угол θ будет меняться, как было показано в гл. 2, п.1. Однако практически заметную связь с высокочастотным полем испытывает только вращающийся магнитный диполь, так как электрического квадруполя заметно слабее. Квантовомеханическое вырыжение для энергетических уровней, эквивалентное классической формуле (8.16) имеет вид
Оно приводит к энергетическим уровням, показанным на фиг. 60, для целых и полуцелых значений I. Легко заметить, что в отличие от ядерных зеемановских уровней, создаваемых магнитным полем, все интервалы между уровнями различны и переходы между соседними уровнями требуют разных радиочастот. Для I = 5/2 должны наблюдаться две резонансные линии с отношением частот 2:1. Обе частоты наблюдались для J127 (спиновое число 5/2) в ряде соединений йода. Отношение частот отличалось от 2 на несколько процентов, и было показано, что это отклонение от 2 измеряет отклонение электростатического потенциала от осевой симметрии. Чисто квадрупольный резонанс можно наблюдать, используя такую же экспериментальную установку, как установка для ядерного магнитного резонансного поглощения, описанная в гл. 3. Образец не обязательно в виде монокристалла помещается внутри катушки, которая создает высокочастотное электромагнитное поле, когда через нее пропускается ток высокой частоты. Любое поглощение радиочастотной энергии образцом можно обнаружить путем измерения уменьшения добротности Q катушки. Если частота ядерного магнитного резонанса определяется напряженностью приложенного магнитного поля, которую можно выбирать свободно, то при чисто квадрупольном резонансе она фиксируется градиентом внутреннего электрического поля в кристалле. Резонансную линию можно обнаружить, меняя частоту высокочастотного электромагнитного поля; поэтому большинство методов ядерного магнитного резонанса непригодно, так как они потребовали бы одновременного изменения настройки ряда контуров. Вследствие этого наиболее удобными оказываются методы с применением регенератора и сверхрегенератора (см. гл. 3, п. 4 и 5). Размеры образца не ограничиваются размерами области однородного поля магнита, но применение больших образцов требует увеличения радиочастотной мощности. Так как при комнатной температуре время спин-решеточной релаксации T1 обычно мало, оптимальные условия обнаружения слабой резонансной линии требуют дальнейшего увеличения радиочастотной мощности. Поэтому сверхрегенератор удобен, так как он может давать большую радиочастотную мощность без возрастания мощности шума. Ширина наблюдаемых квадрупольных резонансных линий занимает интервал от 10^(-2) до 10^(-5) резонансной частоты. Два источника уширения линий являются общими как для ядерного магнитного, так и для ядерного квадрупольного резонанса; это а) магнитное дипольное взаимодействие между соседними ядрами и б) уширение, связанное с малым временем релаксации T1. Третий источник уширения возникает за счет несовершенства кристаллической решетки, в результате которого градиент поля несколько изменяется от молекулы к молекуле. Когда кристалл охлаждается, упругие напряжения внутри него проявляются более резко, и это может вызвать увеличение ширины линии с уменьшением температуры. Четвертым источником уширения являются крутильные колебания молекул, модулирующие градиент электрического поля. Кроме уширения линий, крутильные колебания уменьшают среднее значение градиента электрического поля и, таким образом, уменьшают резонансную частоту. На этом основании Байер предложил объяснение небольшого уменьшения резонансной частоты с повышением температуры, так как амплитуда крутильных колебаний возрастает с температурой. Байер также предположил, что крутильные колебания являются эффективным механизмом, спин-решеточной релаксации, Перечислим теперь те сведения, которые можно получить из измерений ядерного квадрупольного резонанса. Из фиг. 60 видно, что в случае осевой симметрии отношение резонансных частот для двух изотопов, имеющих одно и то же спиновое число, например С135 и С137, в одном и том же кристалле непосредственно дает отношение Q35/Q37 их квадрупольных моментов. При этом предполагается, что электрическое поле для обоих изотопов одинаково (это справедливо с точностью 0,0001). Если спиновые числа двух изотопов различны, то, согласно фиг. 60, отношение резонансных частот равно отношению квадрупольных моментов, умноженному на простой и точно определенный численный множитель. Например, если спиновые числа равны 3/2 и 1, то множитель должен быть равным 2. Если электрическое поле заметно отличается от осевой симметрии, то сказанное выше справедливо для случая одинаковых спиновых чисел изотопов. Если же эти числа разные, то должна быть внесена поправка. Отношения резонансных частот были измерены для следующих пар изотопов: В10 и В11, С135 и С137, Сu63 и Сu66, Br79 и Br81, Sb121 и Sb123, J127 и J129. Точность измерения отношений обычно составляет несколько десятитысячных. Чтобы получить абсолютные значения Q, необходимо рассчитать параметр градиента электрического поля q. Это возможно для простых свободных молекул, и в некоторых случаях объединение молекул в твердом теле имеет небольшое влияние на q междумолекулярные силы должны быть в таких случаях очень слабыми по сравнению с молекулярной ковалентной связью; желательно, чтобы молекулы удерживались вместе только слабыми ван-дер-ваальсовскими силами. Измеряя частоту квадрупольного резонанса для одного и того же ядра в различных молекулах, можно получить относительные значения градиента поля eq в этих молекулах. При помощи таких данных можно получить сведения, касающиеся электронной структуры молекул. Изучение зеемановского расщепления резонансной линии слабыми магнитными полями для монокристалла дает дальнейшие сведения относительно структуры. Этот случай был теоретически изучен Крюгером, Берзоном и Ламаршем и Волковым. Измеряя расщепление для различных ориентации кристалла в магнитном поле, можно найти отклонение электрического поля от осевой симметрии, а также ориентацию главных осей тензора градиента электрического поля относительно кристаллических осей. Большая электрическая квадрупольная связь, обнаруженная в таких кристаллах, как кристаллы иода, в которых для J127 значение e^2Qq/h равно 2153 мггц, дала возможность Паунду использовать такие вещества для определения пространственного расположения ядер. В подходящих для этой цели веществах ядра должны занимать преимущественно уровень m=±I, если они приведены в состояние термического равновесия при температурах, для которых kТ<hν, где ν – частота квадрупольного резонанса. Такие температуры можно получить методом адиабатического размагничивания.
|
 ,
(8.16)
,
(8.16)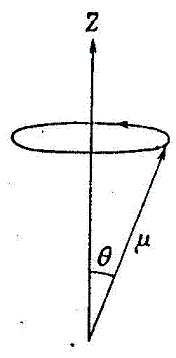
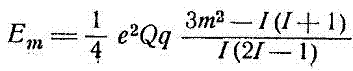 ,
(8.17)
,
(8.17)