При модернизации корпоративных сетей приходится решать задачи их оптимальной цифровизации: выбирать между прокладкой оптического волокна, установкой радиорелейного оборудования или применения аппаратуры, передающей цифровые сигналы по существующему медному кабелю. В статье приводится алгоритм, позволяющий оптимизировать модернизацию сети по конфигурации, пропускной способности и стоимости.

Введение. Сегодня существует достаточно много распределенных корпоративных сетей (КС), охватывающих обширные площади и обслуживающих большое число абонентов. Одна из основных тенденций эксплуатации таких сетей -конвергенция пакетных систем передачи данных (ПД) и мультимедийных сетей. Как следствие - резкое возрастание объема информации, передаваемого по КС, изначально предназначенных для передачи только одного вида трафика, перегрузка сетевого оборудования, отказы различных участков сети.

Многие КС создавались путем хаотичного и непродуманного объединения разнотипных линий связи, в результате получались ненадежные сети, не справляющиеся с возрастающими нагрузками. Постоянное возрастание объема трафика и несовершенство существующих КС делают задачу модернизации и проектирования новых КС предельно актуальной.

Типовая задача, которая стоит при проектировании КС, выглядит следующим образом. Начальные условия:

- действующие сети доступа, которые в КС выступают как абоненты сети, т.е. источники и потребители трафика;

- начальная информация об интенсивности трафика между абонентами сети, предполагаемый рост трафика за расчетный период времени;

- существующие узлы связи, в которых устанавливается коммуникационное и линейное оборудование;

- проложенные линии (как кабельные, так и радиоканалы), информация о возможности создания новых линий связи между различными узлами связи;

- оступный к использованию модельный ряд коммутационного и оконечного сетевого оборудования с их характеристиками.

Необходимо создать поэтапный многолетний план модернизации и развития КС, исходя из заданных ограничений на характеристики качества связи и надежности, предполагаемый рост трафика, подключение новых узлов связи и сетей доступа, ввод в эксплуатацию новых линий связи. Модернизация заключается в строительстве новых и цифровизации существующих аналоговых линий, установке нового, замене или перемещении коммутационного и оконечного оборудования, перераспределении существующих информационных потоков.

Такая динамическая задача поиска оптимальной структуры КС из-за ряда причин достаточно сложна для решения. Основная причина, вызывающая затруднение при решении задачи - ее NP-полнота, и, следовательно, экспоненциальный рост времени поиска оптимальной структуры при увеличении числа узлов сети. Вторая проблема - большая размерность реальных КС, делающая практически невозможным поиск оптимального решения за приемлемое время. Также дополнительная сложность задачи заключается в том, что вследствие длительного времени реализации проектов развития КС необходимо проводить "ступенчатое" проектирование, при котором разрабатывается проект на несколько временных этапов. При этом на каждом этапе модернизации сети должны соблюдаться заданные ограничения на характеристики производительности и надежности, и в целом получаться сеть, оптимальная по конфигурации, пропускной способности и стоимости.

В настоящее время задачи проектирования КС решаются разработчиками на основании собственного опыта без использования автоматических средств структурной оптимизации. Из-за большой размерности задачи сложно проанализировать качество решения, возможность масштабирования получаемых структур. Ошибки, допущенные при проектировании и монтаже различных участков КС, исправлять дорого и долго, и, таким образом, можно сделать вывод о необходимости разработки вычислительного алгоритма поиска оптимальных или квазиоптимальных решений для задачи структурного проектирования КС.

Обобщенная структура КС. На рисунке приведена структура корпоративной сети: СКУ - совокупное коммутационное устройство; УКд - устройство коммутации данных; УКр -устройство коммутации речи; ОУ - оконечное устройство; ЛС - линия связи.

В КС можно выделить две составные части - подсеть доступа и магистральную подсеть. Через подсети доступа к КС подключаются пользователи. Примерами подсетей доступа являются локальные вычислительные сети и учрежденческие телефонные сети. Магистральная подсеть передает транзитный трафик между подсетями доступа. СКУ - это объединение УКр (например, АТС) и УКд (маршрутизатор, коммутатор), установленных в одном узле связи (УС). ОУ представляет собой каналообразующую аппаратуру (мультиплексор, модем), предназначенную для организации виртуальных каналов по линиям связи (медный кабель, волоконно-оптические линии, радиорелейные линии и т.д.).

Узел связи - это организационно-техническое объединение СКУ и ОУ, предназначенных для ввода, вывода информации, каналообразования и коммутации каналов связи в соответствии с потребностью абонентов сети. Магистральная подсеть, соединяющая сети доступа, распределенные на большом географическом пространстве, представляет собой совокупность узлов связи, объединенных линиями и каналами связи. Магистральная подсеть позволяет организовать взаимодействие между абонентами на больших расстояниях. Протяженность ее может составлять сотни и тысячи километров (узлы корпоративной сети могут располагаться в различных городах или странах).

Автоматизация процессов проектирования сети при корректном использовании математического аппарата минимизирует возможность ошибки. Однако не все процессы проектирования поддаются реализации на ЭВМ, в их решении вынужден принимать участие человек-проектировщик, что значительно усложняет задачу оптимизации. В данном случае, представление технического задания в виде, удобном для работы алгоритма, должен выполнять специалист. Наиболее сложная задача - определение приложений, используемых абонентами, и интенсивности информационных потоков, создаваемых этими приложениями. В настоящее время активное сетевое оборудование позволяет проводить мониторинг трафика. На основе таких замеров можно рассчитать средние значения информационных потоков. Это позволит составить матрицу тяготения и сделать определенные прогнозы на возможный рост трафика в будущем.

С математической точки зрения задача оптимизации сводится к отысканию минимума или максимума целевой функции многих переменных при ограничениях на их значения и функциональные связи. Задача оптимального проектирования корпоративной сети представляет собой задачу нелинейного целочисленного программирования, так как целевая функция и ограничения являются нелинейными выражениями, в которых присутствуют целочисленные переменные. Наличие значительных трудностей и специфических особенностей в решении целочисленных и комбинаторных задач оптимизации породило большое количество методов и алгоритмов.

Разработанные методы, в зависимости от требуемого качества получения результата, можно отнести к одному из двух классов: методы, которые всегда приводят к нахождению оптимального решения, но при реальных задачах требуют недопустимо большого числа операций; методы, которые не всегда приводят к нахождению оптимального решения, но требуют приемлемого числа операций. Такие методы позволяют находить квазиоптимальное решение. Точные методы являются наиболее общими, их применяют при небольшой размерности задачи, причем время работы алгоритма находится в экспоненциальной зависимости от ее размерности. Наиболее широко используются методы сокращенного перебора, например, "ветвей и границ" или "неявного перебора". Эти приемы состоят в построении частных решений, представленных в виде дерева поиска, и применении мощных методов построения оценок. Для алгоритмов подобного сокращенного просмотра вариантов характерна организация поиска с возвращением.

Известны и другие подходы, когда процесс поиска организован иначе (иногда они используются совместно с методом "ветвей и границ"). К ним относятся методы динамического программирования и отсечений (отсекающих плоскостей). Реализация данных методов требует больших затрат машинного времени и большой оперативной памяти, поэтому усилия исследователей были направлены на отыскание способов сокращения числа операций и объема ресурсов. Этого удалось достичь ценой отказа от поиска глобального экстремума. Но, хотя такие методы экономичнее, они, как и остальные методы данного типа, бесперспективны для решения задач высокой размерности.

Генетический алгоритм (ГА). При решении задач нелинейной целочисленной оптимизации хорошие результаты показывают методы эволюционного моделирования. Применим для решения описанной задачи один из таких методов -генетический алгоритм.

На стадии математического моделирования КС представляется в виде ненаправленного графа, в котором вершины интерпретируются как устройства связи, ребра - линии связи, веса ребер - соотношение производительности и пропускной способности каналов связи. Коэффициент связности К_св графа зависит от задач, которые выполняет данная сеть, и требований к надежности. При низких требованиях к надежности достаточно древовидной структуры принимается К_св= 1; при требовании высокой надежности К_св= 2 и больше.

Рисунок 1 - Структура корпоративной сети

В сетях связи общего и коммерческого пользования в качестве критерия оптимизации часто применяется стоимость модернизации, которую необходимо минимизировать, а надежность и требования к задержке пакета берутся в качестве ограничений. В процессе оптимизации структуры сети требуется определить топологию сети, множество задействованных линий связи, состав и способ объединения коммуникационных и оконечных устройств.

Все параметры модели разбиваются на три группы: входные, выходные и управляющие.

Входные параметры:

- временной ряд матриц тяготения F(t) = (F(0), F(1),.., F(T — 1),F(T)), где T - число временных периодов, в течение которых проводится оптимизация. Элементами матриц являются средние интенсивности информационных потоков между узлами i,j в момент времени t;

- множество моделей КУ: Н = {h_i}. Характеристики моделей: n(h_i) - число коммуникационных портов; V(h_i) - скорость портов; t(h_i) - время задержки ПД, вносимое КУ; O(k_i) - стоимость обслуживания i-й модели КУ;

- множество моделей ОУ: М = {M_i}. Характеристики моделей: q(m_ij) - скорость передачи ОУ; t(m_i) - время задержки ПД; C(m_ij) - стоимость ОУ для узла связи i в сторону узла j;

- множество типов используемых ЛС: П = {7_i}. Характеристики: М(_i) - множество ОУ, поддерживаемых i-м типом ЛС; С(_i) - удельная стоимость создания 1 км i-ro типа ЛС; O(7T_j) - удельная стоимость владения 1 км i-го типа ЛС;

- L - матрица расстояний между УС;

- Y(0) - начальная топология сети, где y_ij - вектор, определяющий число и тип ЛС между УС i, j в начальный момент времени.

Управляющие параметры:

- временной ряд матриц Y(t) = (Y₀,Y₁,Y₂,...,Y_T), описывающих топологию сети;

- множество установленных и подключенных в i узле связи СКУ: K(t) = (k^t₁, k^t₂,..., k^t_n);

- множество установленных и подключенных в i узле связи ОУ: M(t) = (m^t₁, m^t₂,..., m^t_n).

Выходные параметры:

- суммарные затраты: С^S = S^T_t=0с(t);

- затраты в определенный момент времени:

C(t) = Sⁿ_j=1[y_ij(t) - y_ij(t-1)]l_ijC(p_ij) +

+ Sⁿ_j=1[C(k_j(t)) - C(k_j(t-1))] +

+ Sⁿ_j=1[C(m_ij(t)) - C(m_ij(t-1))] +

+ Sⁿ_j=1y_ij(t)l_ijO(p_ij) + Sⁿ_j=1O(k);

Ограничения на задачу:

- пропускная способность канала связи

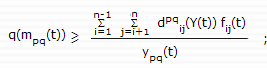
- задержка передачи пакета

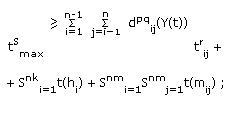
- связность узлов 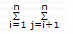y_ij(t) > 1;

- количество портов составных коммутационных устройств

n_j(h_i) > Sⁿ_i=0y_ij, j=0,...,n;

- коэффициент готовности К_r = m/(l + m), где m и l -коэффициенты показательного закона распределения, равные количеству нормально работающих и отказавших устройств сети.

На первом этапе решения задачи с помощью ГА необходимо закодировать переменные задачи в вектор X, называемый хромосомой. Каждый символ х_i, из которых состоит вектор X, является геном хромосомы. Объект о, который имеет определенный набор генов (генотип), однозначно определяющий решение целевой функции, называется особью. Запишем хромосому в следующем виде:

Х = (А₁,А₂,...,А_Т),

где A_i - геномы, описывающие состояние сети в различные временные периоды. Каждый геном

A_i = P(i),H(i),M(i),

где Р(i) - матрица описания физических сред передачи между узлами сети в i-й момент времени; Н(i) - описание множества СКУ в узлах сети в i-й момент (описание представляется в виде вектора, каждый элемент которого описывает СКУ определенного узла); М(i) - описание множества оконечных устройств сети в i-й момент времени.

При образовании новых особей могут возникнуть хромосомы, описывающие запрещенные решения, неудовлетворяющие наложенным ограничениям, например, структуры с изолированными вершинами, древовидные структуры при требовании К_св^2, структуры с большими задержками передачи пакетов и т.д. Для устранения таких структур используется алгоритм ремонта хромосомы, в процессе которого запрещенная структура сети преобразуется в разрешенную. С этой же целью применяются специализированные генетические операторы, позволяющие сразу получать работоспособные структуры сети.

Для определения используемых моделей КУ и ОУ необходимо определить распределение информационных потоков в сети. Для этого на каждом временном интервале случайным образом выбирается некоторое количество ОУ на задействованных ЛС (количество фиксированных ОУ должно быть больше 2 и меньше половины их максимального количества). При этом фиксируется пропускная способность каналов связи с выбранными ОУ. Пропускная способность других каналов считается неограниченной сверху. После этого на полученной структуре решается стандартная задача распределения потоков. Для полученного распределения выбираются оставшиеся незафиксированные ОУ таким образом, чтобы пропускная способность ОУ была больше требуемой пропускной способности канала связи.

Эффективность работы ГА в значительной степени зависит от корректного выбора его параметров - вероятностей применения генетических операторов, методов отбора в следующие поколения, выборе мощности популяции и момента окончания поиска решения. Неправильное определение этих параметров может привести к увеличению времени поиска или существенному ухудшению качества находимого решения.

Один из наиболее важных параметров ГА - начальная мощность популяции. При значительной размерности начального числа особей в популяции увеличивается время генерации новых поколений, и, в конечном итоге, время поиска решения. Оптимальная мощность для каждой сети различна. На основе результатов проведенных экспериментов предлагается использовать следующую зависимость начальной мощности популяции от числа узлов сети:

n^max_p = 10n,

где n_р - мощность популяции; n - количество узлов сети.

Оптимальная вероятность применения операторов ГА также определялась экспериментальным путем. Наиболее близкие к оптимальным - это решения, полученные при вероятности кроссинговера, лежащей в пределах 0,7 < P_cross < 0,8. Вероятность кроссинговера геномов вычисляли при значениях вероятности кроссинговера хромосомы, определенной ранее и лежащей в диапазоне 0,5 < Р_cross < 0,9. Оператор мутации играет роль тонкой настройки найденного решения, во время которой происходит сходимость решения к ближайшему локальному или глобальному оптимуму. При проведении экспериментов по определению значения p_mut вероятность кроссинговера хромосомы фиксировалась P_cross = 0,7, геномов - 0,5.

В разработанном алгоритме схема применения оператора мутации отличается от общепринятой. В данном случае первоначально с вероятностью p_mut определяется, будет ли использоваться оператор мутации к хромосоме. В случае подтверждения мутации, к геномам применяется с определенной вероятностью либо оператор мутации, либо оператор кроссинговера. Как показали опыты, оптимальное значение вероятности мутации лежит в диапазоне 0,4 < p_mut < 0,5. Вероятность использования оператора мутации или кроссинговера к геномам составляет 0,5 и 0,7 соответственно. Для определения вероятностей применения операторов кроссинговера и мутации к геномам использовался тот же метод, что и для определения вероятности кроссинговера и мутации хромосомы. Первоначально была определена вероятность применения оператора кроссинговера, а затем по найденной вероятности применения оператора кроссинговера вычислена вероятность использования оператора мутации.

Мутация может затрагивать одновременно от одного до нескольких ген. Количество ген, подвергаемых мутации и влияющих на эффективность решения, зависит от длины хромосомы. Чем меньше хромосома, тем меньшее количество ген должно подвергаться мутации. Однако слишком большое количество ген, подвергаемых мутации, может существенно увеличить время поиска решения. Количество ген, подвергаемых мутации, находили при ранее определенных вероятностях кроссинговера и мутации. При этом ограничивалось количество поколений (10). Оптимальное количество мутирующих ген в хромосоме - от 1 до 4.

Одним из важных параметров решения задачи методом ГА является выбор точки останова алгоритма. Ранняя остановка алгоритма приводит к ненахождению качественных дешевых решений, а поздняя увеличивает время поиска решений без заметного увеличения качества. Хорошие результаты показал следующий метод выбора точки останова:

n^max_t = 2n^D_t; n^D_t > 50,

где n^max_t - количество поколений, после которых происходит останов алгоритма; n^D_t - номер поколения, во время которого произошло последнее улучшение значения целевой функции.

При создании проектов сетей необходимо соблюдать ограничения на среднюю задержку передачи пакетов и требования двусвязности сети, позволяющие сохранять ее работоспособность при однократном выходе из строя какого-либо участка сети.

Заключение. Полученный алгоритм использовался для создания проектов модернизации корпоративных магистральных сетей на базе медного кабеля. Основными задачами было: определение поэтапного плана установки нового и перемещения существующего цифрового линейного оборудования на проложенных медных линиях; нахождение необходимой пропускной способности отдельных линий и выбор соответствующего оборудования для организации линейного тракта; определение необходимости и сроков временной аренды каналов связи.