Пилипенко Дмитрий Вадимович

Факультет компьютерных информационных технологий и автоматики
Кафедра электронной техники
Специальность: Электронные системы
Тема работы: Обоснование и исследование структуры электронной системы контроля растворенного кислорода аэротенка очистных сооружений
Руководитель: доцент Коренев Валентин Дмитриевич

Кинетика процесса переноса кислорода воздуха при пневматической аэрации природных и сточных вод

Б. ГРИШИН, д.т.н., профессор,
С. АНДРЕЕВ, к.т.н., профессор,
Т. МАЛЮТИНА, ст. преподаватель,
кафедра водоснабжения и водоотведения;
Е. САВИЦКИЙ, доцент кафедры механизации и автоматизации производства,

Источник: Пензенский государственный университет архитектуры и строительства

    Практика эксплуатации современных сооружений аэробной биологической очистки сточных вод показывает, что себестоимость процесса очистки на 60-80 % зависит от эффективности применяемой системы аэрации, являющейся наиболее энергоемким элементом очистных сооружений. В связи с этим оптимизация процесса проектирования и эксплуатации аэрационных систем является весьма актуальной задачей.
   Для создания надежных методов расчета сооружений аэрации сточных вод, необходимо применение современных методов моделирования.
   Наиболее точными, прогнозирующими свойствами, позволяющими получить корректные результаты в широком диапазоне условий проведения процесса, обладают теоретические модели. Теоретическая модель позволяет получить количественную характеристику процесса, основываясь на его основных внутренних физических закономерностях, и как бы является его математическим отражением - «портретом». Поэтому теоретические модели принято называть «портретными моделями», одна из которых была приведена в работе Ю.М. Мешенгиссера и Ю.Г. Марченко «Моделирование процессов при аэрации воды» («Водоснабжение и санитарная техника»).
   В соответствии с этой моделью скорость массопередачи кислорода из газовой фазы описывается уравнением:
  , (кг/с)          (1)
где: К_L - коэффициент массопередачи жидкой пленки (м/с); А - площадь межфазового контакта (м²); С_Н - концентрация насыщения жидкости газом (кг/м³); С - концентрация растворенного в жидкости газа, кг/м³.
   Предполагается определять коэффициент массопередачи жидкой пленки по уравнению Хигби:                           
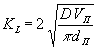   , (м/с)                 (2)
где D - коэффициент диффузии кислорода газа в жидкость,(м²/с); V_П - скорость всплывания пузырька воздуха, (м/с); d_П - диаметр пузырька воздуха, (м).
   Формула Хигби описывает процесс нестационарной молекулярной диффузии через тонкую жидкостную пленку, часть поверхности которой движется вместе с набегающим на пузырек потоком жидкости. Описываемые формулой (2) процессы протекают при переходном режиме всплывания газового пузырька (переход от ламинарного режима всплывания к турбулентному). Нижняя граница переходного режима всплывания воздушного пузырька характеризуется следующими условиями:
 диаметр пузырька воздуха d_П = 0,12·10^-3 м,
 скорость всплывания V_П = 0,0082 м/с;
критерий  Рейнольдса       = 1.
   Коэффициент гидравлического сопротивления, определяемый по формуле: .                               
   Верхняя граница переходного режима всплывания воздушного пузырька характеризуется следующими условиями: d_П = 1,37·10^-3 м; V_П = 0,37 м/с; Re = 500;  = 0,13.
   Пневматические системы аэрации тонкодиспергированным воздухом позволяют получить пузырьки диаметром d_П = 2,5·10^-3-5·10^-3 м, в связи с чем, по нашему мнению, для описания процесса массопередачи этих систем более корректно использовать формулу Данквертса.
   Теория Данквертса описывает турбулентный режим массопередачи (d_П>1,37·10^-3 м), при котором турбулентные вихри, зарождающиеся на поверхности пузырька воздуха, контактируют с ней в течение короткого промежутка времени, в результате чего происходит обновление поверхности границы раздела фаз.
   В соответствии с теорией Данквертса:
                       ,  (м/с)                     (2)
где D_Т - коэффициент турбулентной диффузии, (м²/с); S - фактор обновления границы раздела фаз, (с^-1).
   В своих работах Данквертс не предлагает какого-либо конкретного подхода для определения величины S.
   Одна из попыток по определению численного значения S исходя из анализа баланса энергий (термодинамический подход) была сделана в работе Л.Н. Брагинского, М.А. Евилевича и др. «Моделирование аэрационных сооружений очистки сточных вод» («Химия», 1980). Было высказано предположение, что процесс обновления поверхности раздела под действием турбулентных вихрей, должен быть связан с работой, совершаемой на границе раздела фаз. Поскольку работа, совершаемая при обновлении поверхности, обусловлена наличием поверхностного натяжения, то величина новой поверхности, образующейся в единицу времени за счет турбулентного обмена элементов жидкости на единице поверхности  может быть определена, как , (с^-1)                         (3)
где: Р - работа, совершаемая на единице поверхности в единицу времени (Вт/м²); σ - коэффициент поверхностного натяжения, (Дж/м²):
      и тогда   ,             (4)
где:  ς - коэффициент гидравлического сопротивления при всплывании пузырька воздуха; V_П - скорость всплывания пузырька воздуха, (м/с);  ρ - плотность жидкости, (кг/м³).
   Поскольку S является величиной, обратной среднему времени экспозиции, и может быть интерпретирована как частота обновления поверхности, нами было предложено определять S не в виде отношения элементарной работы Р к коэффициенту поверхностного натяжения  σ, а как отношение секундной работы, совершаемой силами гидродинамического сопротивления А_Т, к поверхностной энергии пузырька воздуха Е.
Здесь   , (Дж/с)  (5)
   , (Дж)                 (6)
где  - сила гидродинамического сопротивления,(Н); Δl (м) - расстояние, на которое перемещается пузырек воздуха за время ΔT , (с);  f_П- площадь поперечного сечения пузырька воздуха, (м²); S_П - площадь поверхности пузырька воздуха, (м²).
   Тогда:  ,  (с^-1 )                    (7)
где - коэффициент формы пузырька воздуха.
   Как видно из формул (7) и (4) предложенное нами уравнение для вычисления значения фактора обновления границы раздела фаз всплывающего пузырька воздуха отличается от формулы (4) лишь наличием дополнительного коэффициента К_ф.
   Введением коэффициента формы пузырька воздуха К_ф учитывается специфика сил поверхностного натяжения F_пн и гидродинамического сопротивления F_г.о. Силы гидродинамического сопротивления действуют на площадь поперечного сечения пузырька воздуха f_П, а силы поверхностного натяжения - на поверхность раздела фаз пузырька воздуха S_П.
   С учетом (7) формула (1) примет вид: 
, (кг/с)             (8)
   Интегрируя уравнение (8) в интервале переменных  δm (от 0 до Δm) и  δt (от 0 до ΔT) имеем:                 
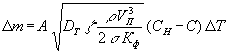,                (9) 
где  Δm  (кг) - масса растворившегося кислорода за время контакта воздуха с водой  ΔT (с).
   Для одиночного пузырька воздуха, имеющего площадь поверхности S_П и объем W_П, величина снижения концентрации кислорода в газовой фазе будет описываться уравнением:                   
  , (кг/м³)     (10) 
где  - дисперсный размер пузырька воздуха, (м).
   Тогда коэффициент использования кислорода воздуха  , определяемый как отношения массы кислорода воздуха, растворенного в воде Δm, к массе кислорода в воздухе, подаваемого в систему аэрации m_кв, может быть вычислен по формуле: 
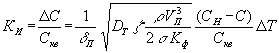,               (11) 
где С_кв - концентрация кислорода в воздухе, кг/м³.
   Время контакта воздуха с водой  ΔT в случае всплывания одиночного пузырька со скоростью V_П в слое жидкости высотой Н, определяется по соотношению:  (с).
   Время контакта  ΔT при одновременном всплывании группы пузырьков уменьшается из-за возникновения эрлифтного эффекта, приводящего к тому, что пузырьки всплывают в слое жидкости, движущейся вместе с пузырьками, и приближенно может быть вычислено по эмпирической формуле:  .    
   Проведенная нами оценка зависимости (11) показала, что она может быть использована для инженерных расчетов окислительной способности (ОС) пневматических систем аэрации с различной дисперсностью пузырьков воздуха:
                ОС = К_u С_кв Q_в , (кг/с),               (12)
где Qв - расход воздуха, подаваемого в систему аэрации, м³/ч.
   Погрешность вычислений окислительной способности систем пневматической аэрации по формулам (11) и (12) не превышает 5% , что вполне допустимо для инженерных расчетов.