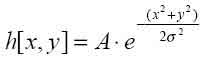 Здесь A – нормирующая константа
(выбирается так, чтобы сумма всех коэффициентов фильтра была равна
единице), ? – «ширина» фильтра, регулирующая степень размытия.
Здесь A – нормирующая константа
(выбирается так, чтобы сумма всех коэффициентов фильтра была равна
единице), ? – «ширина» фильтра, регулирующая степень размытия.
Источник информации: http://graphics.cs.msu.ru/courses/cg02b/library/dspcourse.pdf
Часто некоторые участки на изображении бывают слишком темными, чтобы на них можно было что-то разглядеть. Если прибавить яркости ко всему изображению, то изначально светлые участки могут оказаться совсем засвеченными. Чтобы улучшить вид изображения в таких случаях, применяется метод выравнивания освещенности.
Этот метод не является линейным, т.е. не реализуется линейной системой. Действительно, рассмотрим модель типичную освещенности для фотографии. Фотографируемый пейзаж обычно освещен по-разному в разных точках. Причем обычно освещенность меняется в пространстве достаточно медленно. Мы хотим, чтобы все детали на фотографии были освещены более однородно, но при этом оставались достаточно контрастными друг относительно друга. А на реальной фотографии получается произведение той картинки, которую мы хотим видеть и карты освещенности. Там где освещенность близка к нулю, все предметы и детали тоже близки по яркости к нулю, то есть практически невидимы.
Поскольку освещенность меняется в пространстве достаточно медленно, то можно считать ее низкочастотным сигналом. Само же изображение можно считать в среднем более высокочастотным сигналом. Если бы в процессе фотографии эти сигналы складывались, то их можно было бы разделить с помощью обычного фильтра. Например, применив ВЧ-фильтр, мы бы «избавились от перепадов освещенности» (НЧ-сигнала), а оставили «само изображение». Но поскольку эти сигналы не складываются, а перемножаются, то избавиться от неравномерностей освещенности простой фильтрацией не удастся.
Для решения таких задач применяется гомоморфная обработка. Идея гомоморфной обработки заключается в сведении нелинейной задачи к линейной с помощью каких-либо преобразований. Например, в нашем случае можно свести задачу разделения перемноженных сигналов к задаче разделения сложенных сигналов. Для этого нужно взять логарифм от произведения изображений. Логарифм от произведения равен сумме логарифмов сомножителей. Если учесть, что логарифм от НЧ-сигнала остается НЧ- сигналом, а логарифм от ВЧ-сигнала остается ВЧ-сигналом, то мы свели задачу разделения произведения сигналов к задаче разделения суммы НЧ- и ВЧ- сигналов. Очевидно, эту задачу можно решить с помощью ВЧ-фильтра, который удалит из суммы сигналов низкие частоты. После этого останется только взять от полученного сигнала экспоненту, чтобы вернуть его к исходному масштабу амплитуд.
ВЧ-фильтр можно реализовать следующим образом. Сначала к изображению применяется операция размытия (НЧ-фильтр), а потом из исходного изображения вычитается размытое. Наилучший радиус размытия зависит от конкретного изображения. Можно начать эксперименты с радиуса порядка десяти пикселей.
Обычно для размытия изображения применяется двумерный гауссовский
фильтр, имеющий вид 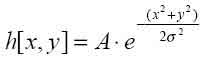 Здесь A – нормирующая константа
(выбирается так, чтобы сумма всех коэффициентов фильтра была равна
единице), ? – «ширина» фильтра, регулирующая степень размытия.
Здесь A – нормирующая константа
(выбирается так, чтобы сумма всех коэффициентов фильтра была равна
единице), ? – «ширина» фильтра, регулирующая степень размытия.
Непосредственное вычисление двумерной свертки с таким ядром требует огромных вычислений даже при сравнительно небольшом размере ядра. Однако приведенное гауссово ядро обладает свойством сеперабельности. Это означает, что эквивалентного эффекта можно достичь, отфильтровав сначала все строки изображения одномерным гауссианом, а затем отфильтровав все столбцы полученного изображения таким же одномерным гауссианом.
Полученный от выравнивания освещенности эффект может оказаться слишком сильным (темные области станут по яркости такими же, как и светлые). Чтобы уменьшить эффект, можно просто смешать обработанное изображение с исходным в определенной пропорции.
