Михаил Болдырев
" Если в руках вдумчивого человека есть лишь молоток, то весь мир представляется ему состоящим из гвоздей..."
Лофти Заде, создатель теории нечетких множеств
Введение.
Вы, наверное, уже обратили внимание, что при решении большинства задач, с которыми сталкиваетесь повседневно, возникает необходимость приближенного задания условий и, соответственно, получаются столь же приближенные ответы. В самых разных сферах деятельности: управление инвестиционными портфелями, планирование финансовой деятельности предприятия, оптимизация товарооборота, оптимизация финансовых потоков, оптимизация информационных потоков, оценка эффективности рекламной компании, оценка влияния политических и социальных событий на поведение рынка, а также многих, многих прочих задачах требуются такие инструменты, которые могут подобные вычисления проводить, причем достаточно быстро и с приемлемой точностью.
Речь далее пойдет об инструментах, использующих принципы нечеткой логики (fuzzy logic). Встречается также другой термин - нечеткое представление(fuzzy thinking).
Постановка задачи.
... Когда Вы управляете автомобилем, двигаясь в плотном городском потоке, Вы заняты разгоном, торможением, маневрированием, соблюдением правил движения и т.д. Если Вас спросить в этот момент, что вы думаете о температуре Ваших тормозов или как Вам смотрится давление масла в гидроусилителе, Вы вряд ли ответите что-то определенное. Вы заняты процессом движения. Все агрегаты автомобиля интересуют Вас постольку, поскольку они способствуют этому процессу. Или не способствуют. У вас просто нет ни времени, ни возможности отвлекаться на детали.
Иными словами, рассматривая Вашу поездку с точки зрения системы, можно сказать, что Вас в большей степени волнуют принципы действия этой системы, то есть насколько способен Ваш автомобиль доставить Вас из точки А в точку Б за заданное время и при заданных известных условиях. И в меньшей степени волнует конструкция этой системы, то есть то, каким способом автомобиль решает эту задачу.
При более детальном изучении вопроса Вы можете заметить, что в подавляющем большинстве задач, которые Вы решаете, входные условия и критерии оценок непрерывно изменяются.
Если уж вернуться к примеру автомобиля, то когда Вы прикидываете расход топлива при езде по городу (целевая функция), Вы строите утверждения примерно так:
В результате вы замеряете средний расход топлива в литрах на 100 км и обнаруживаете, что он существенно отличается от паспортных значений. Вас это отличие не устраивает, но как решить эту проблему ?
Вы допускаете, что Вам в принципе не нужен ответ с точностью до миллилитра. Вам важно просто минимизировать целевую функцию. Иными словами Вы можете для себя определить некоторую степень точности решения задачи, соблюдение которой Вас устроит.
Если Вы зададитесь целью свести значение целевой функции (расхода топлива) к минимуму, причем сделать это, не прибегая к созданию системы, по цене сравнимой со стоимостью автомобиля, Вам понадобится инструмент, который может решать такую задачу при непрерывно меняющихся входных значениях и который может легко подстраиваться под изменение оценочных критериев (например, движение в городе/на трассе). Причем инструмент должен быть прост в управлении и понятен Вам без долгого изучения специальных дисциплин.
Fuzzy thinking. Системы, основанные на принципах.
Прежде, чем приступить к описанию конкретных пакетов, необходимо иметь в виду следующее обстоятельство: пути решения каждой конкретной задачи могут быть весьма разнообразны. Современный математический аппарат предоставляет целый спектр методов, приемов и инструментов для решения практически любой задачи. Все они воплощены в виде алгоритмов в разнообразных программных продуктах.
Приступая к решению очередной задачи и выбирая для нее подходящий "молоток", Вы беспокоитесь не только о самом факте существования решения, но и о эффективности собственно "молотка", то есть о том, за какое время и с какими затратами задача будет решаться.
Существующие подходы к эффективному решению задач таковы:
1. Если Вы знаете правила, по которым действует объект Вашего внимания, вы можете их обобщить и свести в некоторую систему, действующую и генерирующую выводы по схеме "если - то - иначе". Такой подход "на правилах" реализован, например, в техническом анализе и успешно применяется достаточно давно.
2. Если Вы правил поведения объекта не знаете, но подразумеваете их присутствие, то вы создаете систему, которая вначале обучается на некотором множестве примеров (представленных в виде "набор входных значений - критерии оценки - правильные выводы"), а затем адекватно строит выводы на новых входных данных. Такой подход "на примерах" реализован в применении нейросетей и показывает высокие результаты точности оценок и прогнозов.
3. Если Вы не знаете ни правил поведения объекта, ни того, известны ли они вообще и могут ли быть получены, вы пытаетесь смоделировать объект, применяя известные Вам правила и зависимости, что называется, "по аналогии", а затем делаете выводы о том, насколько объект соответствует модели. Такой подход "на моделях" реализован в современной "теории хаоса" и позволяет оценивать события, качественно изменяющиеся за малые промежутки времени.
4. Если правил, примеров и моделей достаточно много, возникают принципы действия объекта - "правила взаимодействия правил (примеров, моделей и т.д.)". То есть Вы можете оценивать и управлять объектом не только на микро-уровне (правила), но и на макро-уровне (принципы). Эти принципы также можно обобщать и сводить к некоторым системам. Этот подход "на принципах" реализован с помощью применения fuzzy-математики в разнообразных инструментальных пакетах: от несложных электронных таблиц до совершенных экспертных систем.
Решение конкретной задачи предполагает комбинации перечисленных подходов.
Коротко перечислим отличительные преимущества fuzzy-систем по сравнению с прочими :
Математический аппарат, предоставляющий такие возможности, детально описан в специальной литературе как комбинация множественных и вероятностных приемов.
В программных пакетах и системах этот аппарат реализован в полной мере, но внешне не виден, спрятан "за кадром", что делает процесс освоения этих инструментов более доступным и интуитивно понятным.
Электронная таблица Fuzi Calc. Быстрые вычисления нечетких данных.
Пакет Fuzi Calc фирмы FuziWare сравнительно молод (1995 год), но успел завоевать популярность как недорогой инструмент, позволяющий проводить быстрые (прикидочные) расчеты в различных областях бизнеса и получать результаты с вполне приемлемой степенью точности.
В составе пакета поставляются несколько примеров решения задач
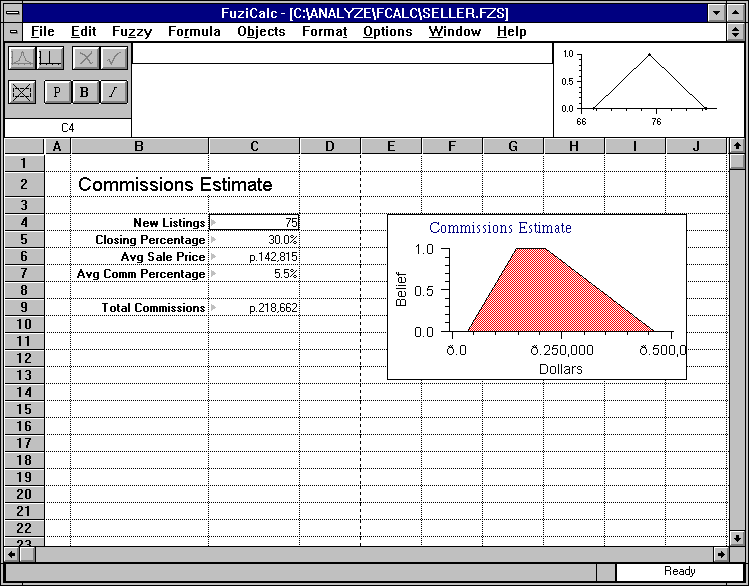
Рабочая среда пакета выглядит так:

На рисунке показан пример решения задачи оценки прибыли при работе фирмы на рынке недвижимости.
Постановка задачи такова: менеджер планирует деятельность фирмы, работающей на рынке недвижимости на следующий год. Целевая функция задачи - диапазон прибыли, на который можно рассчитывать.
Для решения задачи существуют четыре нечетких утверждения, выявленных из статистики деятельности фирмы за несколько прошедших лет:
1. В течение каждого года в фирму приходят примерно 75 потенциальных клиентов.
2. Из потенциальных клиентов примерно 30 % совершают сделки.
3. Стоимость недвижимости, фигурирующей в сделках, составляет примерно $ 142 815.
4. За проведенную сделку с каждого клиента берется примерно 5.5 % комиссионных.
Если просто перемножить эти четыре значения, мы получим цифру $ 176 733. Такова сумма прибыли за год, если ее вычислять обычным способом.
При этом менеджер ясно осознает, что:
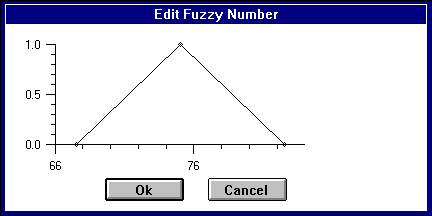
но совершенно точно известно, что никогда не бывало меньше 67 и никогда не было больше 87. (На графике по вертикали - достоверность значения, отложенного по горизонтали)

то есть как правило, это значение изменяется в пределах 25-35%, но никогда не было меньше 10% и никогда не было больше 50 %.

то есть чаще всего происходят сделки по цене $ 138 000 - $ 140 000 , но никогда не дешевле $ 130 000 и не дороже $ 150 000. Обратите внимание на излом графика в зоне, обозначенной пунктирной линией и уход в точку, соответствующую $ 160 000. Здесь менеджер подразумевает, что в следующем году фирма попробует проводить сделки с более дорогой недвижимостью, но не свыше $ 160 000. В противном случае точки перелома не было бы вообще, а график упирался бы в точку, соответствующую цене $ 150 000.

то есть чаще всего их размер лежит в пределах 5-6 % , но не меньше 4 % и не больше 7 % .
Система при такой постановке задачи произведение значений вычисляет перемножением интегралов, описывающих данные кривые. Поскольку типы кривых известны, число их конечно (в системе используется 5 стандартных), то применение 5 стандартных функций, описывающих эти кривые делает вычисления практически мгновенными. Самое главное в том, что изменяя входные значения, Вы не меняете способа их вычисления (системы уравнений, описывающих функции).
В данном примере Вы видите, что, построив 4 нечетких утверждения и перемножив их значения (определение прибыли), ответ можно увидеть так:
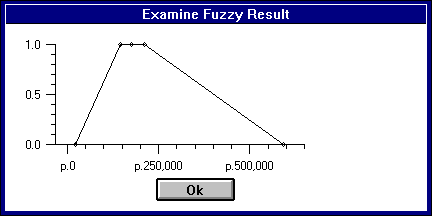
То есть наиболее достоверное значение прибыли будет находиться в пределах $ 150 000 - $ 200 000 (на рисунке обозначена пунктиром). Причем Вы можете увидеть границы: не менее $ 30 000 и не более $ 600 000.
Итак, наш менеджер получил ответ с погрешностью в $ 50 000 в пределах наиболее достоверных значений. При планируемом обороте свыше $ 3 000 000. Устроит ли его такая точность ? Скорее всего, да. И Вас, скорее всего, тоже.
Несколько слов о самом пакете - краткое описание меню:
FILE - стандартные операции с файлами и настройка параметров печати;
EDIT - стандартные операции редактирования и встраивания внешних объектов;
FUZZY - представление числа в ячейке в виде нечеткого распределения (fuzzify) либо в виде обычного числа (crisp). Если в ячейке присутствует серый треугольник слева, значит число задано нечетко. Посмотреть его распределение можно на правом верхнем экране, редактировать - двойной щелчок на соответствующей ячейке;
FORMULA - применение функций, встроенных в пакет (как обычных, так и нечетких);
OBJECTS - операции с объектами - диаграммами нечетких распределений . Имеется полный набор операций: копирование, вырезка, вставка, печать, представление в двух- и трехмерном виде;
FORMAT - изменение графических параметров выделенных объектов: рамки, выравнивание и т.п.;
OPTIONS - общие установки таблицы;
WINDOW- стандартные операции работы с окнами;
HELP - стандартная система помощи, включающая разделы: описание меню, описание функций и работы с формулами, описание нечетких объектов, описание методов связи и встраивания внешних данных.
Теперь представьте такую ситуацию:
Теперь вспомните о небольшой таблице фирмы FuziWare и избавьте себя от лишней головной боли !
Пакет CubiCalc. Управление динамическими системами.
Пакет CubiCalc 2.0 фирмы HiperLogic хорошо известен специалистам, занимающимся задачами динамического управления различными ездящими, летающими и плавающими объектами. Эффективность применения CubiCalc в данных задачах такова, что небезызвестная организация КОКОМ (США), в свое время следившая за тем, чтобы новые американские технологии в компьютерно-программной области не повышали чужой военно-промышленный потенциал, накладывала очень жесткие ограничения на распространение этого пакета ...
В чем причина того, что небольшая черная коробка с двумя дискетами и книжкой внутри совсем недавно приравнивалась к суперкомпьютерам и крылатым ракетам ?
Чтобы пояснить ответ на этот вопрос, мы рассмотрим один из примеров, поставляемых с этим пакетом.
Рабочая среда инструмента выглядит так.
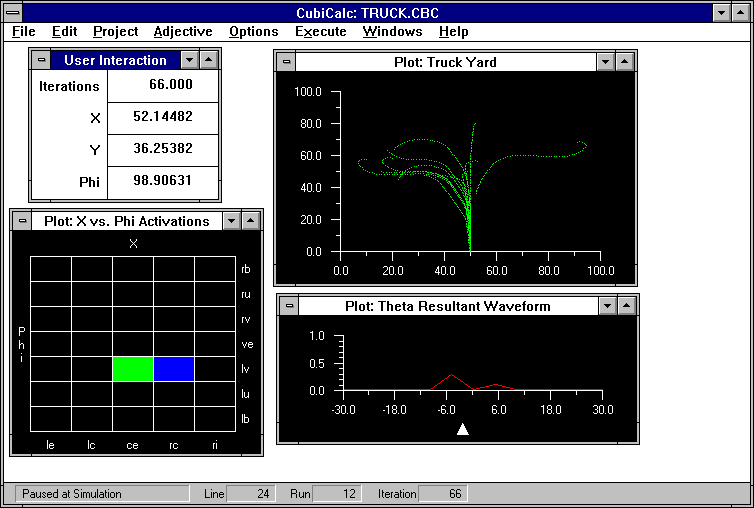
... Пусть простота картинки не вводит Вас в заблуждение: известно, что чем серьезней инструмент и чем на более профессиональную работу он рассчитан, тем меньше авторы помещают в него различных безделушек и финтифлюшек. Перед Вами, если хотите, совершенное оружие, предназначенное отнюдь не для парадов ...
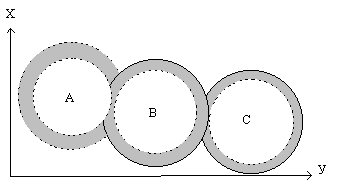
Итак, пример, вошедший во все учебники нечеткой математики. Грузовик заезжает в гараж. Грузовик достаточно длинный, а гараж достаточно узкий (см. рис. ниже).
Тот, кто хоть раз присутствовал при живописной картине маневрирования магистрального трака в узком дворе, может подтвердить: задача нетривиальная.
И если опустить выражения, которыми оперируют участники и очевидцы процесса, то выясняется простой факт: лучшие результаты получаются, когда на подножку трака встает помощник и, пользуясь критериями: "чуть левее...еще левее... СТОП!!!...теперь чуть назад...и вправо...", вместе с водителем достигает искомого результата.

В принципе, задачу можно усложнять сколь угодно: вместо грузовика это может быть тяжелый самолет (тонн этак 70-80), вместо гаража- второй самолет (тоже не маленький), искомый результат - заправка в воздухе, привходящие условия - болтанка и т.д., и т.п. Неважно.
Важно то, что нас с Вами интересуют принципы , по которым может функционировать подобная система, а также то, как эти принципы свести в некоторую систему. Причем задача ставится так, что любой грузовик с любой точки двора при любых условиях (болтанка?) должен заезжать в ворота, расположенные в любом месте двора.
Если задачу решать классическими средствами, то придется писать системы уравнений, описывающих грузовик, гараж, возможные внешние факторы, алгоритмы управления и бог знает что еще. Работа на месяц для целого отдела.
Давайте посмотрим, как такую задачу решает Cubi Calc.
1. Определяем переменные, которыми оперируем. Меню PROJECT/VARIABLES .
На входе замеряем "азимут грузовика относительно ворот" (в градусах, 0...360) и его "смещение относительно оси ворот" (в метрах, 0...100).
Давайте вспомним, что нам важно не замерять углы с точностью до долей градуса, а сводить целевую функцию к минимуму. В данном случае целевая функция - отклонение руля, причем такое, что на въезде в ворота грузовик должен двигаться строго вдоль их оси.
Поэтому на выходе задаем переменную "поворот руля" в градусах (- 30...+30).
Поскольку, как уже было сказано, нам важны принципы, для каждой переменной определим ряд нечетких распределений, соответствующим понятиям "левее-правее" для азимута, отклонения руля и смещения относительно ворот,
Меню PROJECT/ADJECTIVES FOR...
Выглядит это так:
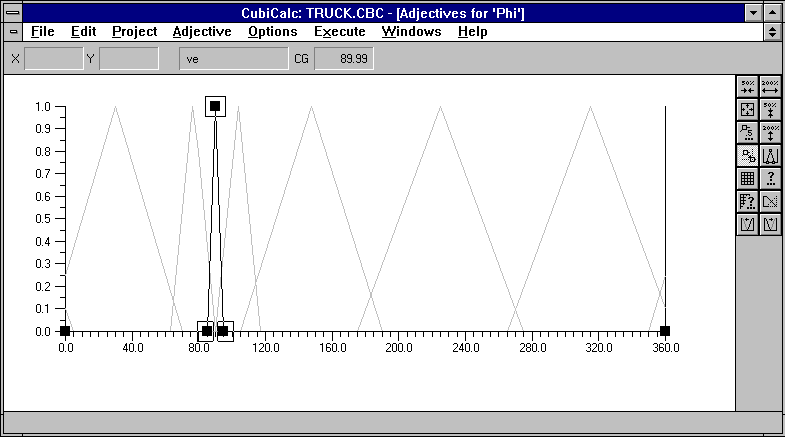
Как видно из схемы, все значения, лежащие между 85 и 95 градусами азимута, соответствуют критерию "точно прямо" (мы полагаем, что ошибка -5...+5 градусов несущественна, т.е. сразу задаем некоторую степень точности).
Здесь же описаны распределения значений азимута, соответствующие критериям "левее, влево, глубоко влево; правее, вправо, глубоко вправо". Для каждого распределения заводится своя внутренняя (temporary) переменная - они нам понадобятся позже, для создания правил.
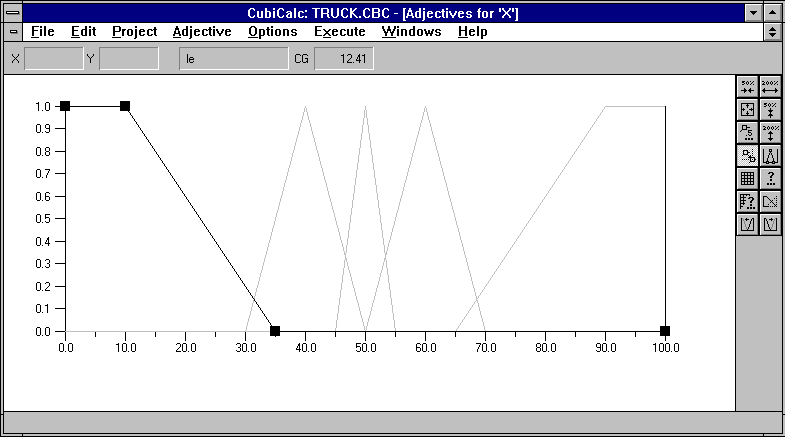
На схеме: критерий "точно в ворота" соответствует значениям между 45 и 55 м (-5...+5 м).
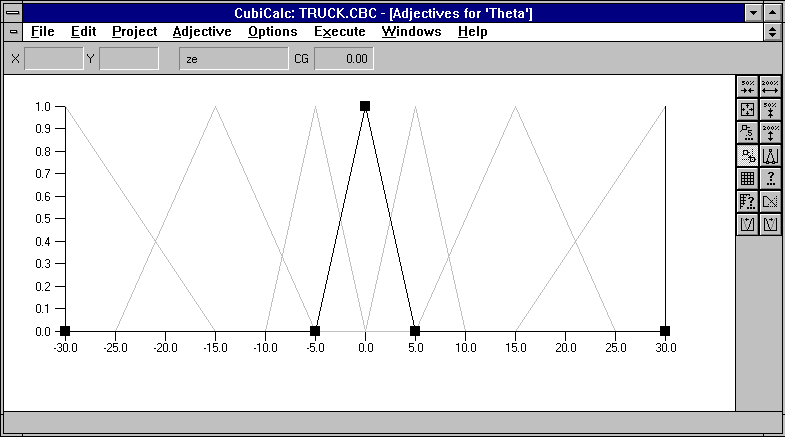
Далее:
мы задаем:
промежуточные переменные (каждому нечеткому критерию "левее", "правее" и т.п. задается своя переменная);
константы, используемые при расчетах (в данном случае - скорость);
О меню PROJECT/RULES следует сказать особо.
Правила (в нашем смысле - принципы) работы системы выглядят так:
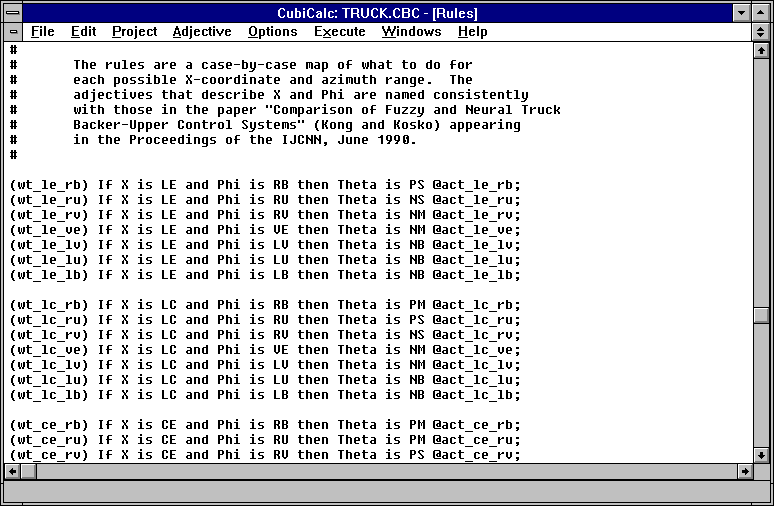
Как Вы можете видеть, правила задаются в форме, интуитивно понятной пользователю:
"если переменная Х имеет значение Y (и/или переменная Z имеет значение F, и/или ...),
то переменная A приобретает значение B ,
иначе переменная A приобретает... и т.д.
Если нос грузовика смотрит влево и сам грузовик находится левее относительно ворот, то надо повернуть руль глубоко вправо и продвинуться на следующий шаг.
То есть стандартная схема "если - то - иначе". С некоторым уточнением: помимо обычных логических операторов "больше", "меньше", "равно", "не равно" присутствуют нечетко логические "очень" (very), "немного"(somewhat).
Для автоматического построения правил существует опция RULEMAKER (поставляется отдельно, о ней будет сказано ниже).
Далее в меню EXECUTE Вы можете запустить полученную систему в непрерывном или циклическом режиме и вывести дополнительный экран для управления системой (см. самый первый рисунок). В процессе работы или в пошаговом режиме Вы можете изменять различные настройки системы?
В версии RTC также предусмотрена возможность компиляции полученной системы в библиотеку dll или в файл с текстом на языке C, что оценят высоко ценят программисты-разработчики сложных систем.
Итак, задача управления грузовиком решена. Времени на ее решение потребовалось чуть меньше, чем написать эти страницы. Разумеется, реальные задачи сложнее и разнообразнее. Причем сложность заключается в том, чтобы правильно формализовать поток данных и выделить в нем переменные. Этому способствует программа Rule Maker.
Тем не менее с помощью Cubi Calc успешно решаются задачи динамического управления в финансовом планировании, технологические процессы, моделирование сложных предметных областей с качественно изменяющимися параметрами, сравнительно-оценочные задачи.
Следует также заметить, что нечеткая математика - как инструмент и как точка зрения, если хотите (отсюда термин fuzzy thinking), относительно молода и предоставляет специалисту широкое поле для экспериментов .
Формализация данных и выявление правил. Программа Rule Maker для Cubi Calc 2.0
Rule Maker - приложение к пакету Cubi Calc. Его назначение - обработка массивов данных, выделение в массивах групп данных по некоторым признакам (кластеризация), выявление связей между выделенными группами (построение правил). Поскольку границы кластеров задаются нечетко, возможны альтернативные выводы с указанием степени их достоверности, то есть оперирование критериями "лучше-хуже", "возможно" и т.д.
Вид рабочей области программы:
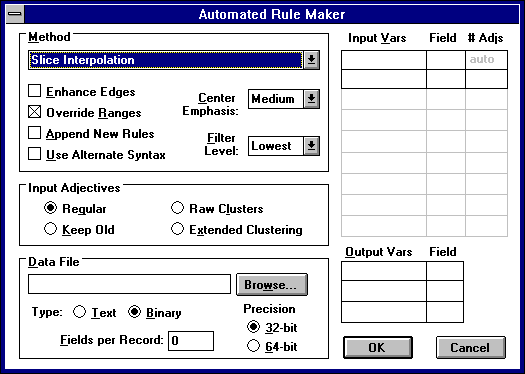
Задача нахождения правил решается в два приема:
1. Кластеризация данных (что само по себе представляет отдельную задачу). Термин "кластер" точно трактуемая как "точка концентрации". То есть под кластеризацией подразумевается нахождений областей (диапазонов значений), где соотношения "вход-выход" встречаются чаще всего. Эти диапазоны описываются как fuzzy-переменные соответственно для входов и выходов. Поскольку границы кластеров описываются нечетко, это позволяет сразу задавать некоторую точность вычислений. (см. рис на примере для двух переменных)
2. Выявление корреляционных зависимостей между входными и выходными значениями (т.н. корреляция "все по всем"). Отличие от классического метода в том, что корреляции ищутся и вычисляются не между изменениями данных, а между изменениями в границах найденных кластеров ! Что и выражается в наборе правил, индицируемом в меню RULES. То есть система опять же оперирует на уровне принципов поведения объекта. В самом деле, присвоив соответствующим входным и выходным переменным названия "больше", "меньше", "хуже", "лучше" и т.д., мы получим набор интуитивно понятных правил, описывающих поведение рассматриваемого предмета.
На рисунке показано, как работает механизм кусочной-линейной интерполяции функции при представлении ее программой Rule Maker. Также возможен механизм сглаженной интерполяции.
В меню программы можно выбрать:
Method:
Input Vars | Field |# Adjs - названия переменных, номера полей в записях, количество кластеров.
Output Vars | Field - соответственно, для выходных переменных.
Data File | Fields per record - тип файла данных (двоичный или бинарный) и количество полей на одну запись.
Input Adjectives - способы кластеризации.
В заключении стоит отметить, что Rule Maker является весьма важной компонентой Cubi Calc и может сэкономить много времени и сил для обработки больших объемов информации.