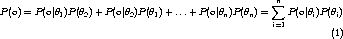
Источник:http://www.generation5.org/content/2004/GAEstimate.asp
Генетический алгоритм - это метод поиска, поиска значения эквивалентного решению поставленной задачи, или близкого к нему. В основе искусственного интеллекта лежит проблеме настройки тренировочного цикла для механизма генерации популяции данных (иногда называемый оценкой параметра), которая является типичной проблемой поиска, поиска параметров, которые позволят адаптировать модель, которая производит данные наиболее приближенные к параметрам тренировочного цикла. Много решений было предложено для различных моделей. В этой статье мы показываем, как оценить параметры смешанного распределения на примере и экспериментально.
Оптимизацией называют поиск ответов, которые лучше всего соответствуют некоторым требованиям. Существует много решений для различных типов проблем оптимизации, таких как сопряженный метод градиента, единично- двоичный метод, симплексный метод и многие другие. Типичное подмножество проблем оптимизации - оценка параметров модели порождающей популяцию данных. Порождающая модель обычно - некоторая статистическая модель, которая аппроксимирует определенную процедуру генерации данных (вот, почему она называется порождающей). Некоторые параметры регулируют небольшие детали процесса генерации данных. Оценка параметра (или тренировка модели в ИИ) приведена в формуле 1, где ряд данных представлен как O, и сгенерирован моделью с параметром Q0, чтобы найти параметры Qi, которые наиболее приближены к Q0, так как мы не уверенны в значении Q0 или незнаем его вообще. Известный метод для оценочных параметров модели, подача ряда частичных данных или содержащих шумы данных, является алгоритмом ожидания максимизации (ОМ). Нужно отметить тот факт что, во многих проблемах поступает лишь часть данных, не потому что они действительно неполные, а потому что мы пытаемся смоделировать их как неполные, таким образом ОМ может быть применен. О другом аспекте, если мы моделируем конечный набор параметров как последовательность хромосомы, то каждый параметр, соответствует гену в хромосоме. Обычно, когда гены имеют дискретные значения, как целые числа, мы можем найти оптимизированный результат при помощи с генетическим алгоритмом (ГА); когда гены имеют непрерывные значения, мы можем найти результат близкий к реальному значению.
В этом разделе мы демонстрируем использование генетического алгоритма для того, чтобы оценить параметры с 2-х компонентного смешанного распределения Гаусса. Смешанное распределение с компонентом n:
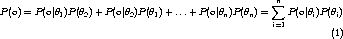
Что означает, для данного наблюдаемого образца O, что он мог быть получен из i-ого компонента P(O|Qi) с вероятностью P(Qi). Вероятность наблюдения О представляет собой сумму вероятностей всех возможных компонентов.
Шаги нашего эксперимента:
1. Выбор модели,
2. Взять образцы О из модели с параметрами Qo,
3. Теперь, забываем Qo и пытаемся найти, Qi которые лучше всего объясняют причину выбора O. В некоторых случаях, значение Qi бывает близко к Qo но это не обычно происходит.
В нашем эксперименте каждый компонент 1D Гаусса, то есть:

Чтобы дать интуитивную визуализацию области проблемы в трехмерном месте, мы сокращаем количество параметра до 2:
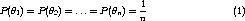
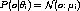
Таким образом, наше смешанное распределение может быть написано как:

Как Вы видите, остались только 2 параметра m1 и m2.
Теперь мы устанавливаем q = 0.3, m1 = 1, m2 = -1. Мы берем 3 образцы от первых компонентов, и 3 от вторых. Смешанное распределение и взятые образцы показаны на рисунке 1.
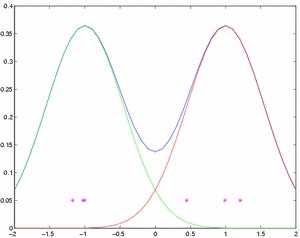
Рисунок 1 - Упрощенная модель смешанного распределения и 6 образцов
С известным типом модели (не параметрами), мы можем вычислить вероятность между образцами O={o1,02,...,o6} и данным набором параметра {Q1,Q2}. Так как каждое oi может быть получено от любого из 2 компонентов, то у соответствующего компонента из 6 О, обозначенного как Q={Q1,Q2,…,Q6} будут 64 комбинаторных значения, обозначенные как х. Вычисление вероятности происходит исходя из того что, 6 поколений и компоненты независимы друг от друга.

Решение проблемы путем грубой силы состоит в том, чтобы перечислять все возможные парные параметры {Q1,Q2}. К сожалению этот метод непрактичен, потому что диапазон Q бесконечен. Но это может бать использовано, для визуализации области решений на рисунке 2.

Рисунок 2 - Визуализация вероятности между всеми возможными парами параметров и 6 взятыми образцами
Есть два нюанса на этом рисунке, которые нужно отметить
На рисунке 2 видно, что мы хотим попасть в место расположения одного из двух пиков. Если мы решим эту проблему другими методами, например используя ЕА алгоритм, то мы по-прежнему начнем с одного положения, приближаясь к пику с каждым повторением. С ГА мы начинаем с популяции стартовых позиций - каждый индивид в популяции представлен своей хромосомой - последовательностью генов. В нашем примере хромосома состоят из двух генов, один для Q1, а другой для Q2. С каждым новым повторением соответствующее значение вычисляется для каждого индивида в популяции. В нашем примере мы выбираем наиболее вероятное значение из возможных на рисунке 2, и генетические операции применяются к текущей популяции:
1. Элитизма (с высокой вероятностью 6 взятых образцов из О) выживут – они будут скопированный в популяцию следующего поколения,
2. Слияние - некоторое индивиды создадут потомков, посредством слияния данных родителей,
3. мутация - дети мутируют, добавляет случайное число ко значениям Q1 и/или Q2.
Рисунок 3 показывает значение вероятности вместе с результатом каждого повторения нашего генетического алгоритма. Сегменты красной линии показывают процесс приближение к одному из пиков.
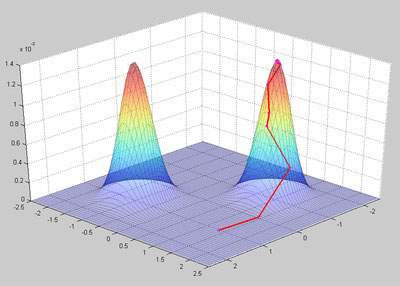
Рисунок 3 - Результат гентического алгоритма