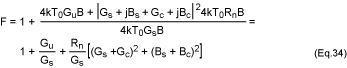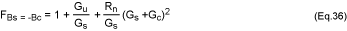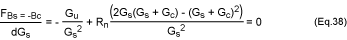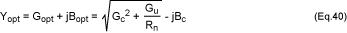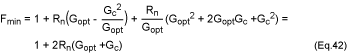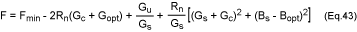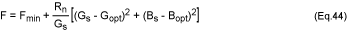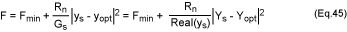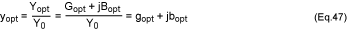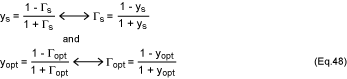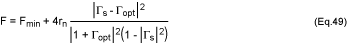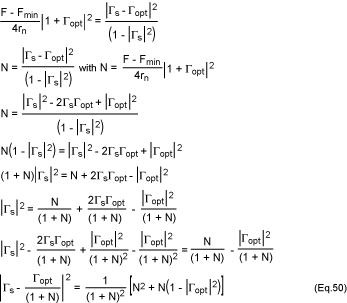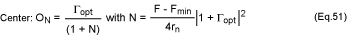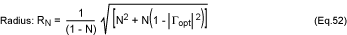Low-Noise Amplifier (LNA) Matching Techniques for Optimizing Noise Figures

Maxim Innovation Delivered

Source of information: http://pdfserv.maxim-ic.com/en/an/AN3169.pdf

Abstract 

An RF amplifier is an active network that increases the amplitude of weak signals, thereby allowing further processing by the receiver. Receiver amplification is distributed between RF and IF stages throughout the system, and an ideal amplifier increases the desired signal amplitude without adding distortion or noise. Unfortunately, amplifiers are known to add noise and distortion to the desired signal. In a receiver chain, the first amplifier after the antenna contributes most to the system noise figure. Adding gain in front of a noisy network reduces the noise contribution from that network.

Amplifier Noise Figure

To analyze the effect of circuit noise, one can model the noisy circuit as a noiseless circuit plus external noise sources. For a noisy, two-port network with internal noise sources (Figure 1a), the effects of those sources are represented by the external noise-voltage sources V_n1 and V_n2, placed in series with the input and output terminals, respectively (Figure 1b). Those sources must produce the same noise voltage at the circuit terminals as the internal noise sources. The values of V_n1 and V_n2 are calculated in equations 1 and 2. Representing the noise-free, two-port network in Figure 1b by its Z parameters:



and:



Equations 1 and 2 show that the V_n1 and V_n2 values can be determined from open-circuit measurements in the noisy two-port network. It follows from these equations that when the input and output terminals are open (I₁ = I₂ = 0) (equations 3 and 4):



and:



In other words, V_n1 and V_n2 equal the corresponding open-circuit voltages.

                                                                            
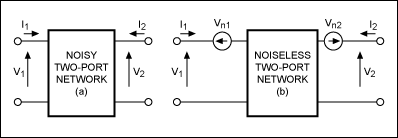
                                        Figure 1. A noisy two-port network (a) can be modeled by a noise-free two-port network (b) with external noise voltage sources V_n1 and V_n2.

In an alternate representation of the noisy two-port network (Figure 2), the external sources are the current noise sources I_n1 and I_n2. Equations 5 and 6 represent the noise-free two-port network:



and:



The values of I_n1 and I_n2 in Figure 2 follow from short circuit measurements taken in the noisy two-port network, as shown in equations 7 and 8:

                                                                            
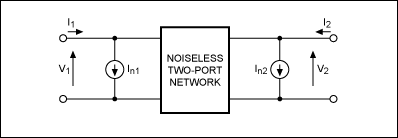
                                        Figure 2. A noisy two-port network can also be represented by a noise-free, two-port network with external noise-current sources I_n1 and I_n2.



and:



Other representations, besides those shown in Figures 1b and 2, can be derived for a noisy, two-port network. A convenient representation for noise analysis places the noise source at the input of the network (Figure 3).

                                                                              
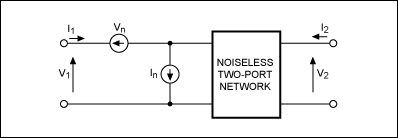
                               Figure 3. Again, a noisy, two-port network can be represented as a noise-free, two-port network with external noise sources V_n and I_n at the input.

Representing the noise-free, two-port network in Figure 3 by its ABCD parameters in equations 9 and 10 show:



and:



Equations 9 and 10 show that there is no simple way to evaluate V_n and I_n in Figure 3, using open- and short-circuit measurements. From a practical point of view, those values (V_n and I_n) can be expressed in terms of noise voltages V_n1 and V_n2 in Figure 1b (which require only open-circuit measurements).

The relationship between noise sources V_n and I_n in Figure 3 and noise sources V_n1 and V_n2 in Figure 1b is derived as follows. Using Z parameters to represent the noise-free, two-port network in Figure 3:



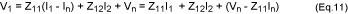
and:



Comparing equations 1 and 2 with equations 11 and 12, it follows that:



and:



Hence, solving equations 13 and 14 for V_n and I_n gives:



and:



An alternate method for determining V_n and I_n relates them to noise sources I_n1 and I_n2 in Figure 2. It is easy to show that the relations in this case are:



and:



A source connected to the noisy two-port network (Figure 4) is represented by a current source with admittance Y_s. It is assumed that noise from the source is uncorrelated with noise from the two-port network. Thus, noise power is proportional to the mean square of the short-circuit current (denoted by active-low I_sc²) at the input port of the noise-free amplifier; and noise power due to the source alone is proportional to the mean square of the source current (active-low I_s²). Hence, the noise figure F is given by:



                                                                            
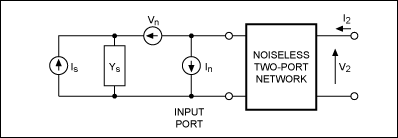
                                      Figure 4. This noise model lets you calculate the amplifier noise figure.

Because I_sc = -I_s + I_n +V_nY_s, it follows that the mean square of I_sc is given by equation 20:



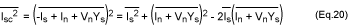
Because noise from the source and noise from the two-port network are uncorrelated:



and equation 20 reduces to:



Substituting equation 20 into equation 19 gives:



There is some correlation between external sources V_n and I_n. Hence, I_n can be written as the sum of two terms—one uncorrelated to V_n (I_nu) and one correlated to V_n (I_nc). Thus:



Furthermore, the relation between I_nc and V_n in terms of a correlation admittance Y_c is defined as:



Y_c is not an actual admittance in the circuit; it is defined by equation 25 and calculated as follows. From equation 24:



Multiplying equation 26 by V_n*, taking the mean, and observing that :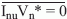



Substituting equation 26 into equation 23 produces the following expression for F:



Noise produced by the source is related to the source conductance by:



where G_s = Re[Y_s]. The noise voltage can be expressed in terms of an equivalent noise resistance R_n as:



and the uncorrelated noise current can be expressed in terms of an equivalent noise conductance G_u:



Substituting equations 29, 30, and 31 into equation 28, and letting:



and:



gives:



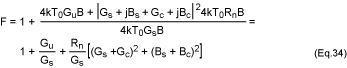
The noise factor can be minimized by properly selecting Y_s. From equation 34, F is decreased by selecting:



Hence, from equation 34:



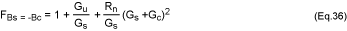
The dependence of the expression in equation 34 on G_s can be minimized by setting:



This gives:



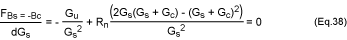
Solving for G_s:



The values of G_s and B_s in equations 39 and 35 give the source admittance, which results in the minimum (optimum) noise figure. This optimum value of the source admittance is commonly denoted by Y_opt = G_opt + jB_opt; that is:



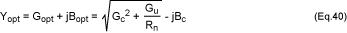
From equation 36, the minimum noise figure F_min is:



Solving equation 39 for G_u/G_opt and substituting into equation 41 gives:



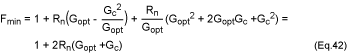
Using equation 42, equation 34 can be expressed as:



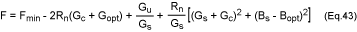
Solving equation 39 for G_u and substituting into equation 43, the expression for F can be simplified:



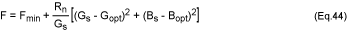
Equation 44 shows that F depends on Y_opt = G_opt + jB_opt, and on F_min. When these quantities are specified, the value of noise figure F can be determined for any source admittance Y_s. This equation can also be expressed as:



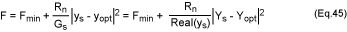
where m = R_n/Z₀ is the normalized noise resistance and y_s = Y_sZ₀ is the normalized source admittance:



y_opt is the normalized value of the optimum source admittance:



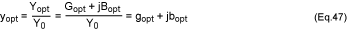
Admittances y_s and y_opt can be expressed in terms of reflection coefficients:



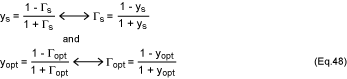
Expressing y_s and y_opt in terms of reflection coefficients helps formulate the noise figure (equation 45) as a function of those coefficients. This formulation is more convenient for industrial LNA applications because in most data sheets, the LNA characteristics are expressed as a table of S parameters and the optimum reflection coefficient G_opt vs. frequency:



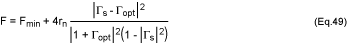
When the noise figure is expressed as a function of a circle, it can be used with a Smith chart for optimum noise-figure matching in specific applications:



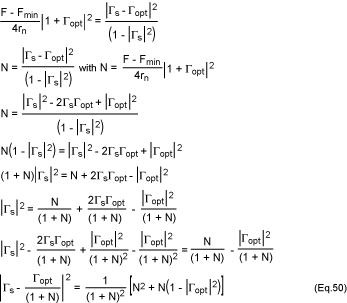
For LNA input matching, a noise circle is positioned on the Smith chart as follows:





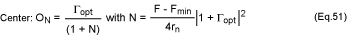
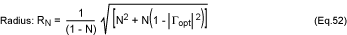
From equations 51 and 52, one can visualize the noise performance of an LNA by plotting the noise circles on the Smith chart. This technique allows the designer to see the effect of tuning in order to estimate the practical noise performance.

Designing for Optimum Noise Figure

For any two-port network, the noise figure measures the amount of noise added to a signal transmitted through the network. For any practical circuit, the signal-to-noise ratio (SNR) at its output is worse (smaller) than at its input. In most circuit designs, however, the noise contribution of each two-port network can be minimized through a judicious choice of operating point and source resistance.

The preceding section demonstrates that for each LNA (indeed, for any two-port network), there exists an optimum noise figure. LNA manufacturers often specify an optimum source resistance in the data sheet. As an alternative, data sheets for the MAX2656 and other LNAs specify an optimum source-reflection coefficient.

To design an amplifier for minimum noise figure, determine (experimentally or from the data sheet) the source resistance and bias point that produce the minimum noise figure for that device. Then force the actual source impedance to "look like" that optimum value with all stability considerations still applying. If the Rollet stability factor (K) is calculated to be less than 1 (K is defined as a figure of merit for LNA stability), then you must be careful in choosing the source and load-reflection coefficients. For an accurate depiction of the unstable regions, it is best to draw stability circles.

After providing the LNA with optimum source impedance, the next step is to determine the optimum load-reflection coefficient (Γ_L) needed to properly terminate the LNA's output:



where Γ_S is the source-reflection coefficient necessary for minimum noise figure. (The asterisk in the above equation indicates the conjugate of the complex quantity Γ_L.)

Applications

A practical example to illustrate the theory of optimum noise matching for LNAs is the MAX2656 - an LNA (Figure 5) with high third-order adjustable intercept point (IP3). Designed for PCS phone applications with gain selected by logic control (14.5dB in high-gain mode and 0.8dB in low-gain mode), the amplifier exhibits an optimum noise figure of 1.9dB (depending on the value of bias resistor R_BIAS). The MAX2655/MAX2656 IP3 is adjusted with a single external bias resistor (R_BIAS), which lets you optimize the supply current for specific applications.

                                                                                   
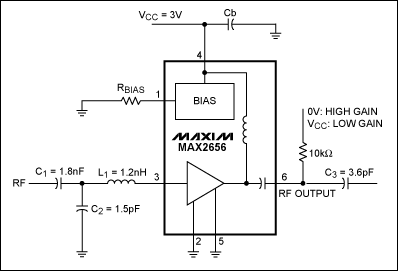
           Figure 5. This typical operating circuit for the MAX2656 LNA shows design values for the  input-matching network.

Figure 5's application employs a MAX2656 LNA operating at a PCS receiver frequency of 1960MHz and noise figure of 2dB (as requested by design). It must operate between 50Ω terminations. As described in the MAX2656 data sheet, the optimum bias resistance (R_BIAS) for minimum noise figure is 715Ω. The optimum source-reflection coefficient Γ_OPT for minimum noise figure in a 1960MHz application (F_MIN = 1.79dB) is:



A source impedance with noise-equivalent resistance R_N = 43.2336Ω yields the minimum noise figure.

A MAX2656 LNA operating at 1960MHz has the following S parameters (expressed as magnitude/angle):

- S₁₁ = 0.588/-118.67°
- S₂₁ = 4.12/149.05°
- S₁₂ = 0.03/167.86°
- S₂₂ = 0.275/-66.353°

The calculated stability factor (K = 2.684) indicates unconditional stability, so we can proceed with the design. Figure 5 shows design values for the inputmatching network. First, a Smith chart for input matching shows (in blue) the 2dB constant-noise circle requested by design (Figure 6). For comparison, note the dotted-line depiction of constant-noise circles corresponding to the noise figures of 2.5dB, 3dB, and 3.5dB.

                                                                                                         
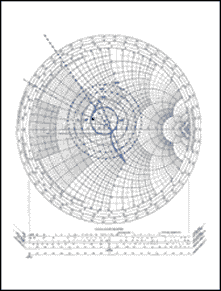
                              Figure 6. The solid circle on this Smith chart depicts the desired (optimum) 2dB noise figure for a MAX2656 PCS LNA with input matching.

For convenience, we chose a source-reflection coefficient of Γ_S = 0.3/150° on the 2dB constant-noise circle. The normalized 50Ω source resistance is transformed to Γ_S using two components: the arc Γ_SA (clockwise in the impedance chart) gives the value of series inductance L₁. Arc BO (clockwise in the admittance chart) gives the value of shunt capacitor C₁.

The value of arc Γ_SA measured on the plot is 0.3 units, so Z = 50 x 0.3 = 15Ω. Thus, L1 = 15/ω = 15/(2πf) = 15/[2π x (1.96 x10⁹)] = 1.218nH, rounded to 1.2nH. The value of the arc BO measured on the plot is 0.9 units, so 1/Y = Z = 50/0.9 = 55.55Ω. Thus, C₂ = 1/(55.55 x ω) = 1/(55.55 x 2πf) = 1/[55.55 x 2π x (1.96 x 10⁹)] = 1.46pF, rounded to 1.5pF.

C₁ is simply a high-valued DC-isolation capacitor and does not interfere with the input matching. The chosen Γ_S provides the load-reflection coefficient needed to properly terminate the LNA:



This value and the normalized load-resistance value are plotted in Figure 7, which also shows a possible method for transforming the 50Ω load into Γ_L. For this example, note that a single series capacitor provides the necessary impedance transformation.

                                                                                                         
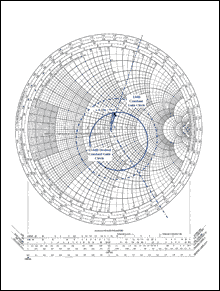
                       Figure 7. The MAX2656 PCS LNA has output matching for a desired (optimum) 2dB noise figure.

The arc OΓ_L (counterclockwise in the impedance chart) gives the value for series capacitor C₃. The value of arc OΓ_L measured on the plot is 0.45 units, so Z = 50 x 0.45 = 22.5Ω. Thus, C₃ = 1/(22.5 x ω) = 1/(22.5 x 2πf) = 1/[22.5 x 2π x (1.96 x 10⁹)] = 3.608pF, rounded to 3.6pF.

Conclusion

1. Gonzalez, Guillermo; Microwave Transistor Amplifiers, Analysis & Design; Second Edition, Prentice Hall, Upper Saddle River, New Jersey 07458.
2. Bowick, Chris; RF Circuit Designs; Howard W. Sams & Co. Inc., a publishing subsidiary of ITT.
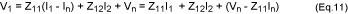
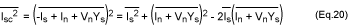
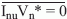