Досліджено алгоритми/ оптимального резервування, а саме, визначення пошуку кількост! резерв-них елемент\в для показників нaдiйності R- i T-muniв із заданою кількістю обмежень в тепекомунікаційних системах i мережах. Визначивши топологію мережі й «вузькі місця», вирішується завдання використання резервних каналів зв'язку и обхідних маршрутів з різними типами показників надійносі й наявністю обмежень.
Вступ Контроль якості — одне з основних завдань, яке необхідно вирішувати для будь-якого піддприємства. Одним з основних критеріїв якості є надійність, тобто властивість системи зберігати в часі у встановлених межах значения вcix параметрів, що характеризують здатність виконувати необхідні функції в заданих режимах i умовах експлуатації [1]. Підвищувати якість функціонування телекомунікаційних систем i мереж можна різними способами.
Один з них — піддвищувати їx надійність. Як правило, методи проектування мереж передачі інформації, зводяться до того, що, маючи на вході piзні характеристики компонент мережі, у тому числі й характеристики їx надійності, визначити топологію мережі й обчислити надійність у цілому. Телекомушкаційні системи можна віднести до систем, що складаються з великої кількості піддсистем. Як правило, розглянуті системи зв'язку є послідовним з'еднанням взаємозамінних ділянок, або однотипних, але рознесених у npocтopi.
3i збільшенням складності системи зв'язку імовірність виходу з ладу будь-якого її компонента збільшується. Сучасні системи зв'язку використовують велику кількість елементів, що робить необхідним використання обхідних маршрутів i резервування для під-вищення коефіцієнта готовності системи зв'язку в цілому. Резервування — метод піддвищення надійності об'єкта шляхом введення додаткових елементів i функціональних можливостей понад мінімально необхідних для нормального виконання об'єктом заданих функцій [1].
При вирішенні задач резервування в телекомунікаційних системах зв'язку, постає проблема не тільки забезпечити задані показники, але й зробити це економніше, тобто з найменшими сумарними витратами на резервні елементи для системи в цілому [2].
Метою цієї роботи є знаходження алгоритма оптимального введения надмірності в системи з довільною структурою одразу за двома показниками — ефективності та вартості. Змінюючи ефективність i вартість кожного елемента системи, оптимізуеться ефективність i вартість системи в цілому.
1. Визначення задач оптимального резервування На практиці виникають ситуації, коли потрібно максимізувати надійність при декількох обмеженнях або мінімізувати витрати для надлишкових елементів при заданій сукупності вимог до надшності окремих телекомунікаційних підсистем. Як обмеження можуть виступати такі величини: R(xly...,xm) — показник надійності системи за умови, що на і-й ділянці є резервні елементи; Т(xt,...,xm) — середній наробіток до відмови за умови, що на і-й ділянці є резервні елементи. Для різних сполучень вищенаведених показників можливі такі формулювання задач оптимального резервування [3]:
1. Одне обмеження з показником надійності типу R У цьому випадку показник надшності системи визначається у вигляді добутку відповідних показників надійності окремих ділянок
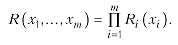
За наявності одного обмежувального фактора в умовах сформульованого завдання можлива постановка таких задач:
а) роздільним резервуванням системи досягти показника надійності не менше заданого RQ ІЗ мінімально можливою вартістю резерву в цілому
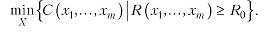
б) роздільним резервуванням системи, що складаеться з т д1лянок, досягти того, щоб при максимально можливому показнику надійності системи R (або при мінімально можливих показниках Q або L) вартість усього резерву не перевищила заданого значення C0
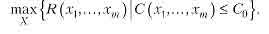
Надалі R будемо інтерпретувати в термінах імовірностей безвідмовної роботи для невідновлюваних систем. Однак простою заміною цих імовірностей відповідними коефіціентами готовності (або коефіціентами оперативної готовності) можуть бути розв'язані оптимальні задачі i для відновлюваних систем.
2. Одне обмеження з показником надійності типу Т. У цьому випадку показник надійності системи

Можна сформулювати дві задачі:
а) Пряма задача. Роздільним резервуванням системи, що складається з т ділянок, досягти того, щоб значення середнього наробітку до відмови було не меншим від заданого То з мінімально можливою вартістю резерву в цілому, тобто
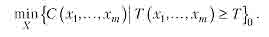
б) Зворотна задача. Роздільним резервуванням системи, що складаеться з т ділянок, максимізувати середній наробіток до відмови Т за умови, що вартість резерву не перевищить заданого значення CQ
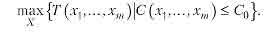
3. Кілька обмежень з показником надійності типу R.
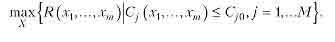

Виходячи з формули (6) i економічних показників на практиці припускають
4. Багатофункціональна схема з декількома обмеженнями. Для багатофункціональних систем вимоги до надійності задаються у вигляді набору Нехай є М обмежень, наприклад, на вартість, масу, габаритні розміри тощо, які повинні бути виконані одночасно. Використовуючи введені позначення, можна сформулювати задачу значень імовірності виконання кожної з цих функцій. (Значення цих імовірностей залежать від важливості й відповідальності відповідних функцій.) Виконання кожної функції залежить від працездатності певних елементів системи, причому в загальному випадку підмножини елементів, необхідні для реалізації різних функцій, можуть мати й спільні частини (перетинатися). При цьому може бути сформульована така задача: роздільним резервуванням системи, що складаеться з т ділянок, домогтися, щоб iмовірності виконання системою кожної з К функщй були не меншими від заданих значень при мінмальній загальній вартості резерву
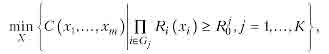
де Gj — підмножина елементів, працездатність яких необхідна для виконання j-ї функції; Щ — необхідне значения ймовірносі виконання j-iї функції.
2. Алгоритм оптимального введення надмірності в системи з довільною структурою Далі розглянемо алгоритм оптимального введения надмірності в системи з довільною структурою. Розглянемо деяку систему, що складаеться з п елементів. Кожен i -й елемент може перебувати у двох станах: у стані працездатності (Sj = 1) i в стані відмови (Si = 0). Тоді в довільний фіксований момент часу система може перебувати в одному з 2" різних станів S = (S1,S2, ..., Sn), де Sі приймають значення 0 або 1. Показник ефективності Е складної системи визначається як
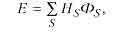
де Hs — імовірність S-го стану системи; Фs — показник умовної ефективності системи в S-му стані, піддсумовування здійснюється за всіма індексами S . Імовірність Hs може бути легко розрахована в припущенні незалежності окремих елементів
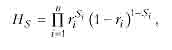
де ri; — iмовірність працездатного стану i -го елемента у фіксований момент часу.
Будемо розглядати систему, елементи якої можуть бути виконані декількома різними варіантами; наприклад, і-й елемент може мати варіант і1, і2,..., іj,, ... Кожний і1, j-й варіант i –го елемента характеризується двома показникам: надійності гДг,-) i вартістю сДг') . Передбачається, що для кожного елемента варіанти утворюють опуклу вгopi домінуючу послідовність. Розглянемо задачу оптимального розподілу наявної вартості між елементами системи для того, щоб домогтися максимального показника ефективності Е. Попередньо визначимо залежність показника Е від надійності кожного з елементів системи. Використовуючи (11), формулу (10) можна записати у вигляді
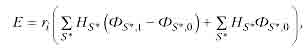
де S* — стан системи без обліку і-го елементу; S*, 0 и S*, 1 — стани системи, коли вci елементи, крім і-го, перебувають у стані S*, а і -й перебувае в стані Si = 0 або Sj = 1 відповідно. Зрозуміло, що величини Hs* не залежать від ri. Таким чином, з формули (12) бачимо, що показник ефективності Е є лінійною функцією ri. Розв'язання задачі зводиться до оптимального підвищення надійності елементів для збільшення показника ефективності Е системи при обмеженнях на сумарні витрати С0 (або для рішення зворотного завдання: мінімації сумарних витрат системи при обмеженні на показник Е0). Для визначення елемента, надійність якого доцільніше всього підвищувати з погляду оптимізаци показника ефективності системи в цілому, обчислюемо величини.

де Е\ i Q — відповідно значення показника ефективності й вартості системи на першому кроці оптимального процесу за умови, що з метою підвищення надійності варіант г0 замінений варіантом ц , i = 1,2,..., п.
Далі визначаеться номер елемента к, відповідний величині
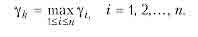
У даного елемента здійснюється заміна варіанта ^на k\ i вважаеться, що початковий стан перед другим кроком характеризується Е = Ek i С = С^ . Подібний процес триває далі, тобто

На N-му кроці процесу система складається з таких варіантів елементів: nin(N) (ТУТ Ji(N) — індекс, що означає порядковий номер варіанта і-го елемента на N-му кроці процесу), а й вартість
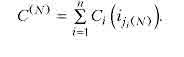
Імовірно, що ЛГ=^/ДЛГ), тому що на кожному кроці процесу один з елементів міняє г=1 номер варіанта на одиницю.
Значения у\ + можна легко обчислити, використовуючи вирази (12) и (16)
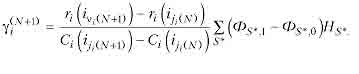
Якщо елементи системи мають високі показники надійності, такі, що і - й — для п вcix i = 1,2,..., п, то можна записати

де ФЕ — умовний показник ефективності системи за умови, що вci елементи п працездатні, тобто для St = 1, S2 = 1 ,•••, Sn = 1; ФЕ* s =о ~ умовний показник ефективностi системи за умови, що вci елементи i"i, кpiм ^-го, працездатні, тобто для St = 1. Висновки
Сформульовано задачі оптимального резервування, а саме, визначені алгоритми пошуку кількості резервних елементів для показників надійності R- i Г-типів i3 заданою кількістю обмежень. Дане питания є досить актуальним для телекомунікаційних систем i мереж, тому що, маючи інформацію про топологію мережі й «вузькі місця», використовуються резервні канали зв'язку й обхідні маршрути з різними типами показника надійності й наявності обмежень. На практиці, визначаючи завдання оптимального резервування для телекомунікаційних систем, найчастіше розглядається алгоритм розв'язання багатофункціональних систем з декількома обмеженнями або резервування з декількома обмеженнями для показника надійності типу R.
СПИСОК ЛІТЕРАТУРИ
1. Черкесов Г. Н. Надежность аппаратно-програмных комплексов / Учебное пособие. 1-е изд.. — С-Пб., 2004 г.
2. Комарницкий Э. И. Надежность работы волоконно-оптических сетей связи и оперативное устранение аварий // LIGHTWAVE Russian Edition. — 2005 г. — № 4.
3. Надежность технических систем: Справочник / Ю. К. Беляев, В. А. Богатырев, В. В. Болотин и др.; Под ред. И. А. Ушакова. — М.: Радио и связь, 1985.