ЭВОЛЮЦИОННОЕ ВЫЧИСЛЕНИЕ НА ОСНОВЕ ЗАДАЧИ МНОГОКРИТЕРИАЛЬНОГО ПЛАНИРОВАНИЯ ПРОИЗВОДСТВЕННОГО ПРОЦЕССА

Авторы: G. Zhou, M. Gen

Перевод: Солодуха О.В.

Источник: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.17.1651

Аннотация - задача планирования производственного процесса (ППП), распространена среди производственных систем. В общем, задача может быть решена с помощью сетевого анализа или динамического программирования. Но в случае многокритериального планирования производственного процесса (коротко мППП) традиционным методам оптимизации трудно справиться с этим. В этой статье рассматривается новый эволюционный вычислительный (ЭВ) подход, который решает задачу ППП с единственными или множественными целевыми функциями. Предлагаемые ЭВ подход придерживается нового простого шифрования состояния перестановки и объединяется с методом поиска окрестности операции мутации, чтобы улучшить эволюционный процесс поиска оптимального решения задач ППП. Численный анализ показывает, что предлагаемое эволюционное вычисление очень эффективно для проблемы ППП.
Ключевые слова - планирование производственного процесса, многокритериальная оптимизация, эволюционное вычисление.

1. Введение

Задача планирования производственного процесса (ППП) распространена среди производственных систем. Задача обеспечивает детальное описание производственных способностей и требований для преобразования необработанного запаса материалов в завершенный продукт через многоступенчатый процесс. Задача ППП поддается методам оптимизации для того, чтобы найти лучший план производственного процесса между многочисленными альтернативами, получившими определенный критерий, такой как минимальная стоимость, минимальное время, максимальное качество или с несколькими этими критериями. Неявное перечисление всех этих альтернатив может быть сформулировано как сетевой поток. В случае единственного целевого критерия задача эквивалентна нахождению кратчайшего пути, которая может быть эффективно решена с помощью некоторых алгоритмов, таких как Дийкстра и Флойеда. Однако, в случае множественной целевой функции (т.е. при мППП) некоторые методы, основанные на целевом программировании, развивались, но только были представлены с помощью маленьких сетей [14] [15] .
Недавно подход, основанный на генетическом алгоритме (ГА), для решения задачи ППП был представлен в [1], где было принято шифрование двоичных строк для представления хромосом. Двоичные строки были признаны эффективными для некоторых задач [5] [6] [10], но они не всегда работают хорошо. В [1] усложненная модификация, которая принимается для генетических операций как начальная популяция или потомок, сгенерированный с помощью кроссинговера или мутации, может быть нелегальной в большинстве случаев, которые воздействуют на эффективность эволюционного процесса в подходе, основанном на ГА.
Эволюционное вычисление (ЭВ), основанное на ГА, принимает естественное кодирование, такое как переменная точка или естественная перестановка, чтобы представить задачи реального мира и развивать их к оптимальному решению, соединенному с генетическими операциями [3] [7] [13]. Этот новый подход широко и успешно применяется в разнообразных исследовательских областях [8] [9] [12]. В этой статье показано развитие задач ППП и мППП. Новое шифрование непосредственно кодирует выбранное состояние на каждой стадии средствами перестановок, которые бывают только длиной n-1 для n-стадии задачи ППП, поэтому сохраняется большая часть памяти и повышается вычислительная эффективность. Достоинство нового кодирования состоит в том, что любая общая генетическая операция на этом кодировании не будет генерировать нелегального потомка таким образом, что ему не потребуется модификация как для начальной популяции, так и для потомка, сгенерированного в эволюционном процессе. Кроме того, легко смешать это новое кодирование с некоторыми эвристическими операциями мутации, такими как метод поиска окрестности, чтобы эффективно эволюционировать к оптимальному решению. Эксперимент на нескольких тестовых задачах показывает, что предлагаемый метод эффективен для ППП с единственными или множественными целевыми функциями.
Задача мППП и ее математическая модель описаны в разделе 2. В разделе 3 описано новое кодирование для мППП. В целом ЭВ подход рассмотрен в разделе 4. В разделе 5 проанализированы тестовые проблемы на новом кодировании и ЭВ подходе и заключение следует в разделе 6.

2. Описание задачи мППП

Система ППП обычно состоит из серии машинных операций, таких как превращение, бурение, перемалывание, полировка и т.д., для превращения части в ее финальную форму или продукт. Целый процесс может быть разделен на несколько стадий. На каждой стадии есть множество подобных производственных операций. Задача ППП - найти оптимальное планирование процесса среди всех возможных альтернатив, получивших определенный критерий, такой как минимальная стоимость, минимальное время, максимальное качество или несколько этих критериев, которые определены на операции для выбора. Как пример, рисунок 1 показывает простую задачу ППП, решаемую средствами сетевого потока.

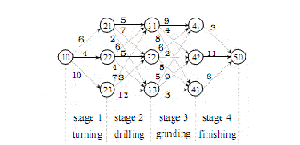
Рисунок 1: Сетевой поток для простой проблемы ППП

Для n-стадии задачи ППП, пусть Sk будет некоторым состоянием на стадии k, Dk(Sk) - множество возможных состояний, которые могут быть выбраны на стадии k, k=1,2,..,n. Затем задача ППП может быть сформулирована так:

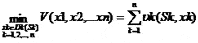(1)

где vk(Sk,xk) - критерий для определения xk при состоянии Sk на стадии k, обычно определен как реальное число, например, стоимость, время или расстояние.
Уравнение (1) может быть записано как динамическое рекурсивное выражение, как показано на рисунке 1 оно может быть принято методами кратчайшего пути или динамического программирования. Однако, в случае множественного целевого критерия уравнение (1) принимает следующий вид:

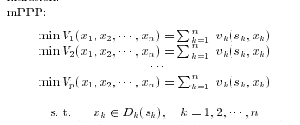(2)

где р - число критериев. Уравнение (2) обозначено как задача мППП.
Очевидно, что сложно преобразовать выражение (2) в его эквивалент динамического рекурсивного выражения для решения методом кратчайшего пути или динамического программирования. Относительно проблемы маленького масштаба, уравнение (2) может приблизиться к некоторому традиционному многокритериальному решению, полученного методами, например, целевого программирования. Однако, если масштаб проблемы возрастет, станет сложно иметь дело даже в случае единственного целевого критерия из-за быстрого расширения числа состояний, которые должны рассматриваться, не говоря уже о случае множественного целевого критерия. Поэтому необходимо развивать новый подход к решению задачи мППП. В следующем разделе мы обсудим наш эволюционный вычислительный подход.

3. Кодирование состояние перестановки

Когда рассмотрение сетевого потока выражения (1) показано на рисунке 1, интуитивно описать планирование процесса с помощью указания какой узел или состояние выбирается для специфических операций на каждой стадии. Если узел или состояние выбрано, это обозначается "1", если не выбрано, обозначается как "0". Таким образом, решение ППП может быть зашифровано в формате двоичной строки с помощью объединения всех состояний множества на стадиях, которые показаны на рисунке 2.

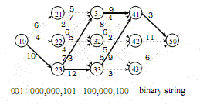
Рисунок 2: Кодирование двоичных строк для задачи ППП

Так как на последней стадии всегда только одно состояние, которое выбрано, это не требует кодирования. Хотя двоичным кодированием строк можно управлять без окружении ГА, неизбежным является то, что в начальной популяции или потомке, сгенерированном в процессе эволюции, будет более чем два возможных планирования процесса, закодированных одновременно одним кодированием, или ни одного возможного закодированного планирования процесса. Поэтому требуются более усложненные модификации для операций ГА, включающих как "идентификатор пути", так и "множественный корректор пути" [1].
Фактически, относительно задачи ППП, показанной на рисунке 1, альтернативные состояния на каждой стадии могут быть выражены сериями целых чисел для указания узла или состояния. Если состояние для операции выбрано на той же стадии для планирования процесса, то передача целого числа для того узла или состояния может быть назначена, тогда как целое число - в пределах номера возможных состояний на той стадии. Поэтому решение ППП может быть кратко закодировано в формате состояния перестановок объединением всех состояний множества на стадии, как показано на рисунке 3.
Это кодирование состояний перестановок один к одному отображает распределение для задачи ППП, поэтому его легко раскодировать и оценить. Сравнивая с двоичным кодированием строк, это кодирование состояний перестановок имеет три ценных преимущества:
(1) длина кодирования равна только n-1 для n-стадии задачи ППП, которая состоит в сохранении большой части памяти, пока масштаб проблемы растет;
(2) кодирование не требует никаких модификаций в генетических операциях, таких как кроссинговер или мутация, которые также повышают вычислительную эффективность;
(3) кодирование легкое для смешивания с некоторыми эвристическими генетическими операциями, чтобы улучшить процесс эволюции.

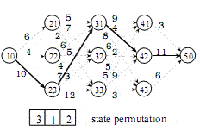
Рисунок 3: Состояние перестановок для задачи ППП

4. Эволюционный вычислительный подход

А. Генетическое представление
Так как он был рассмотрен в предыдущем разделе, кодирование состояния перестановок более применимо для ППП. Те три преимущества гарантируют кодирование состояние перестановок, которое приспосабливается к генетической операции в ЭВ подходе. Относительно начальной популяции для n-стадии задачи ППП, каждый индивидуум - это перестановка с n-1 целыми числами, тогда как каждое целое число генерируется случайно с номером всех возможных состояний на передаваемой стадии.

Б. Генетическая операция
Хотя любая общая генетическая операция в кодировании состояния перестановок не даст результат в нелегальном потомке, мы придерживаемся операции мутации в ЭВ подходе, так как операция кроссинговера не имеет большого эффекта в задаче ППП, что будет продемонстрировано в экспериментальном анализе в разделе 5. С другой стороны, для этого кодирования состояния перестановок легко смешать метод поиска окрестности в операции мутации для получения улучшенного потомка. Рисунок 4 показывает пример для такой операции мутации с методом поиска окрестности, полагая, что ген мутирует на стадии 3 и выбранное число возможных состояний равно 4.

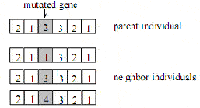
Рисунок 4: Мутация с поиском окрестности

В.Оценочное вычисление
В случае задачи ППП с единственной целевой функцией мы можем непосредственно рассчитать фитнес значение каждого индивидуума в соответствии с целевой функцией выражения (1). Однако, относительно задачи мППП мы можем только рассчитать каждое целевое значение выражения (2), но не можем вычислить его фитнес значение, так как эти множественные критерии обычно конфликтуют друг с другом на практике. Другими словами, мы не можем получить абсолютное оптимальное решение, но мы можем получить оптимальное решение Парето. Здесь, мы принимаем некоторое множественное критериальное решение по методу [4], чтобы вычислить фитнес функцию для задачи мППП.
Определение 1. Дан набор допустимого решения Х для выражения (2), решение х? € Х обозначено как оптимальное решение Парето (не превалирующее решение) для выражения (2) тогда и только тогда, если нет любого другого решения х € Х, удовлетворяющего следующим условиям:

Vq(x) Vk(x)<=Vk(x') для всех k<>q

Определение 2. Относительно выражения (2), при оптимизации каждой целевой функции min Vk(x), k=1,2,…p, соответственно р оптимальное решение хj, j=1,2,…,р, и передача целевого значения:

Vkj=Vk(xj), k=1,2,…p, j=1,2,…p

В целевом пространстве, хотя то р указывает Vk=(Vk1,Vk2,…Vkp) (k=1,2,..p), существует гиперактивная плоскость, которая удовлетворяет:

Sum(bkVk)=a, k=1..p

где a и bk (k=1,2,…р) - решения следующих равенств:

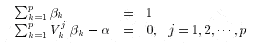(3)

Эта гиперплоскость обозначена как адаптивная целевая вычислительная гиперплоскость для выражения (2).
Вышеуказанное уравнение (3) имеет (р+1) переменную и (р+1) линейных уравнений. Не трудно проверить, что существует уникальное решение, если не существует абсолютного оптимального решения для выражения (2).
Используя эту адаптивную целевую вычислительную гиперплоскость, мы можем вычислить фитнес значения выражения (2) в смысле многокритериальности и следить за соблюдением оптимального решения Парето, чтобы получить близкую к идеалу цель настолько, насколько это возможно. Вычислительным процессом можно управлять следующим образом:
процедура: вычисление для мППП
шаг 1: декодировать все индивидуумы и рассчитать их целевые значения в каждой задаче.
шаг 2: определить bk (k=1,2,…р) в соответствии с Определением 2.
шаг 3: определить фитнес значения вычисления (х) всех индивидуумов в соответствии со следующей формулой:

Относительно задачи мППП с двумя критериями, механизм вычисления в эволюционном процессе может быть реализован, как показано на рисунке 5. Адаптивная целевая вычислительная гиперплоскость разделяет область поиска на две части. Одна содержит оптимальное решение Парето и идеальную точку, которая недостижима, а вторая только содержит доминирующие решения. С эволюционным процессом и под давлением операций селекции, адаптивная целевая вычислительная гиперплоскость обновляется снова и снова, и перемещается к идеальной точке, чтобы осуществить приближение всех решений Парето к идеальной точке настолько, насколько это возможно. Наконец, все решения Парето достигают своей границы.

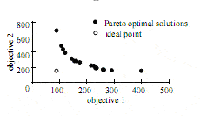
Рисунок 5: Изображение вычисления

Г. Выбор
Здесь мы принимаем (m+l) стратегию выбора [2]. Но для того, чтобы избежать преждевременных сходимости эволюционного процесса, наша стратегия выбора только выбирает m разных лучших индивидуумов из m родителей и l потомков. Если нет доступных m различных индивидуумов, свободный пул популяции заполняется восстановленными индивидуумами, сгенерированными случайным образом.

5. Численный анализ

Прежде всего, мы провели несколько численных экспериментов на задаче ППП. Численный пример с простой задачей, представленный Б. Авадом и др., подробно рассмотрен в [1]. Проблема включает 7 стадий, 24 узлы, 80 дуг и общую численность в 1440 возможных планирований производственных процессов. Это выдано, как показано на рисунке 6.

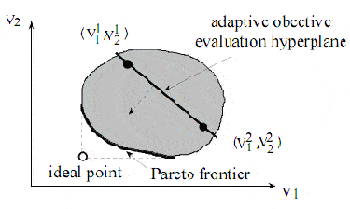
Рисунок 6: Изображение численного примера с 7 стадиями и 24 узлами

Для этого простейшего примера, с использованием двоичных строк и установлением размера популяции pop_size: 200, в наилучшем случае оптимальное решение может быть найдено на 5 генерации и в среднем работа эволюционного процесса имеет выравнивание от старта только после 21 генерации в 20 случаях [1]. Однако, с использованием кодирования состояния перестановок и предлагаемого ЭВ подхода, оптимальное решение может быть в среднем получено на 4 генерации для малейшей популяции размером pop_size: 5 и на 3 генерации для более длинных популяций размером pop_size: 50. С тех пор, как кодирование состояния перестановок стало намного проще, чем кодирование двоичных строк для этой задачи, это действительно забирает не много усилий в эволюционном процессе, чтобы развиваться к оптимальному решению. Рисунок 7 ясно показывает эволюционный процесс кодирования состояния перестановок под действием предлагаемого ЭВ подхода, который начерчен в соответствии со средними результатами в 20 испытаниях.

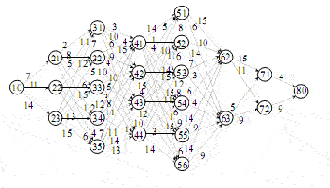
Рисунок 7: Изображение эволюционного процесса с использованием ЭВ подхода

Относительно анализа для установочных параметров генетических операций, мы вычисляем более длинный масштаб задачи ППП, которая состоит из 15 стадий, 89 узлов, 562 дуг, на которых веса - целые числа, генерируемые случайным образом и единообразно распространенные на участке [1, 50]. В соответствии с результатами эксперимента, кроссинговер реально имеет небольшой эффект на эволюционный процесс для ЭВ подхода к этой проблеме. Если только операция кроссинговера принята, ни одного оптимального решения не может быть получено в 20 испытаниях. Что касается операции мутации, она проводится с большой вероятностью получить оптимальное решение независимо от того, что кроссинговер одновременно принята или нет. Рисунок 8 четко показывает чувствительность операций кроссинговера и мутации на предлагаемом ЭВ подходе и указывает, что скорость мутации в пределах от 0,6 до 0,9 имеет наилучший механизм для эволюционного процесса.

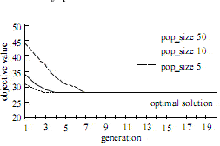
Рисунок 8: Изображение чувствительности кроссинговера и мутации

Результаты эксперимента показывают, что в ЭВ подходе к задаче ППП операция кроссинговер (равномерный кроссинговер или точечный кроссинговер) не дает достаточно новых генов для эволюционного процесса, чтобы развиваться к оптимальному решению. Только операция мутации генерирует серии новых генов, необходимых в эволюционном процессе, и гарантирует развитие к оптимальному решению, пока будет совмещенной с методом поиска окрестности. Более того, слишком низкая мутационная скорость не в состоянии сделать достаточной мутацию на некоторых генах для эволюции; пока слишком высокая мутационная скорость дает результат в слишком большом случайном порядке волнения на индивидуумах таким образом, что потомок имеет больше шансов потерять их сходство с родителями, и алгоритм теряет способность выучится из истории поиска. Когда мутационная скорость равна 0,7 - 0,8, ЭВ подход имеет большую вероятность развиваться к оптимальному решению данной проблемы.
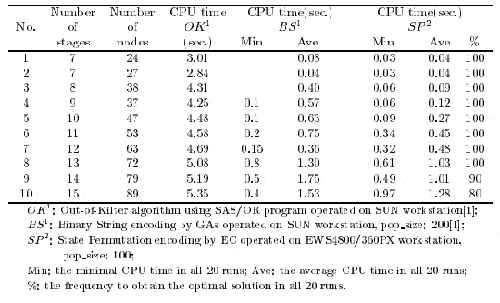
Для того, чтобы в дальнейшем показать эффективность предлагаемого ЭВ подхода на проблеме ППП, мы сгенерировали 10 различных задач ППП, которые имеют одинаковый масштаб как в [1]. Все результаты сведены в таблице 1. Для того, чтобы сравнить 2 разных ЭВ подхода на одной проблеме, есть несколько факторов, которые взяты в рассмотрение. Кроме того, различные установки параметров, таких как скорость кроссинговера, скорость мутации, размер популяции, количество генераций и количество пробегов, различный мягкий и вычислительный смыслы также очень важны для вычислительных сравнений. Однако, сравнивая результаты экспериментов в [1], таблица 1 по-прежнему ясно показывает, что наш ЭВ подход эффективен для проблемы ППП.
Наконец, давайте обсудим проблему мППП. Основанная на численном анализе задачи ППП с единственной функцией, более длинный масштаб проблемы мППП с 15 стадиями и 89 узлами спроектирован. Два атрибута определены на каждой дуге, чьи веса - целые числа, генерированные случайным образом и единообразно распространенные на участке [1, 50] и [1, 100] соответственно. Идеальная точка это (91,159) и две другие экстремальные точки (оптимальное решение Парето) - (91,686) и (402,159). Потому что есть различные атрибуты, определенные на каждой дуге, невозможно получить идеальную точку как оптимальное решение. Мы можем только получить оптимальное решение Парето проблемы мППП. Используя адаптивную целевую вычислительную гиперплоскость как фитнес функцию, результаты предлагаемого ЭВ подхода изображены на рисунке 9.

Рисунок 9: Изображение задачи ППП

Рисунок 9 ясно показывает, что адаптивная целевая вычислительная гиперплоскость играет очень важную роль в руководстве поиском идеальной точки в эволюционном процессе для случая многокритериальной целевой функции, и реально осуществляет поиск всех оптимальных решений Парето, полученных к идеальной точке так близко, как только возможно и сфокусированных на границе Парето возле идеальной точки. Это обычно результаты некоторых надежд решительных творцов в принятии многокритериального решения.
Таблица 1: Сравнение среди различных подходов к проблеме ППП

6. Заключение

Эта статья представляет новый подход к решению задачи ППП с использованием метода ЭВ. Предлагаемый ЭВ подход принимает новое кодирование состояний перестановок для того, чтобы сделать эволюционный процесс даже более простым в нахождении оптимального решения, и объединяется с методом поиска окрестности для получения большой вероятности приблизиться к оптимальному решению. Численный анализ показывает, что предлагаемый ЭВ подход конкурентоспособен по отношению к традиционным методам сетевого анализа в решении этого типа задач. Сравнивая с другими подходами, основанными на ГА, предлагаемый ЭВ подход эффективен в отношении к этому типу задач с единственными или множественными критериями.