Соловьёв М.С., Воропаева В.Я. Прогнозирование трафика GSM сетей с учётом свойств фрактальности

ПРОГНОЗ ТРАФИКА GSM СЕТЕЙ С УЧЁТОМ СВОЙСТВ ФРАКТАЛЬНОСТИ

Соловьёв М.С., Воропаева В.Я.

Донецкий Национальный Технический Университет, кафедра АТ

Источник: Проблемы Телекоммуникаций – 2008 / Материалы II международной научно-технической конференции. – Киев, КПИ – 2008, с.99-101.

Операторы телекоммуникационных услуг, в том числе и мобильных, стремятся повысить эффективность использования установленного оборудования при сохранении высоких показателей качества предоставляемых услуг. Экспериментальные исследования указывают на специфическую природу процессов в телекоммуникационных сетях, которые не укладывается в традиционные рамки теории телетрафика. Характерным для описания процессов передачи данных пакетным трафиком являются обнаруженные на практике свойства самоподобия или фрактальности (масштабной инвариантности) статистических характеристик.

Для прогноза трафика GSM сети необходимо сделать математическое описание, которое будет учитывать свойства фрактальности трафика.

Постановка задачи прогнозирования и её решения заключается в том, что данные прогноза о пропускной способности позволяют получить дополнительные сведения для решения различных задач управления сетью, а именно формирование алгоритма предотвращения перегрузок.

Как показали исследования, трафик сети обладает свойствами самоподобия. Разделим отрезок на три равные части (ξ=1/3). Отбрасываем открытую среднюю часть, оставляя слева и справа от неё два отрезка длины 1/3. Применим эту процедуру к оставшимся отрезкам, получаем четыре отрезка длины (1/3)².Далее мы продолжаем подобную процедуру разделения на отрезки, и доходим до n-ого этапа разбиения к отрезкам длины δ_i=(1/3)ⁿ, i=1,N общим числом N=2ⁿ. Мера определяется из формулы (1) при L₀=1

Эта мера не расходится или не стремится к нулю, если В=β. Указанному условию соответствует 2ⁿ(1/3)^nβ=1 или β=ln2/ln(1/ξ)=ln2/ln3. Мы получили канторовское множество, которое является фракталом, его размерность имеет дробную величину. В процессе разбиения исходного отрезка часть состояний (отрезков) невозвратно теряется.

Выберем импульсную переходную характеристику вида которая пронормирована на единицу: . Процессу u(t) на выходе системы с полной памятью соответствует процедура усреднения на интервале (0,t) временной оси . Исходный интервал делится на три части. Отбрасываем среднюю часть, оставляя слева и справа от неё два подинтервала длины ξt. Координаты оставшихся подинтервалов (0, ξt) и (2ξt,t). В результате перенормировки на единицу плотности состояний после первого этапа разбиения 1/2ξt. На n-m этапе разбиения имеем 2ⁿ подинтервалов, каждый длины ξⁿt. Плотность состояний в таком случае будет определятся выражением 1/(2ξ)ⁿt. Интеграл будет иметь вид , где единичная функция принимает значение 1 при , и 0 при . Для построения канторовского множества является прямоугольник с площадью, равной размеру файла X=λt – количество посланных за время t данных. Ему соответствует результат интегрирования , при f(τ)=λ. На первом этапе разбиения при ξ=1/3 количество переданных данных 2ξλt, потерянных – ξλt. На n-м этапе разбиения (2ξ)ⁿλt и λt[1-(2ξ)ⁿ]. После предельного перехода n→∞ количество переданных данных вычисляется из выражения 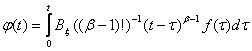, которое после замены переменных t-τ=y и f(τ)=λ будет иметь вид . Данный интеграл нормирован на единицу, поэтому число переданных пакетов λt^β оказывается меньше числа посланных – λt. На передачу недосланых пакетов потребуется затратить время t^1/^β-t. Таким образом мы имеем возможность получить достоверный прогноз об общем количестве информации, выделить необходимый для этого ресурс, что позволит более рационально использовать канал связи.

Таким образом, сформировано математическое описание свойств фрактальных процессов применительно к телекоммуникациям; полученные результаты свидетельствуют о том, что для получения достоверного прогноза можно передавать часть информации, а затем выделять требуемый ресурс для выполнения задачи.

Литература

1. А.Я, Городецкий, В.С. Заборовский Фрактальные процессы в компьютерных сетях. СПб: 2000.

2. Peitgen H.O., Richter P.H. The beauty of Fractels. Springer – Verlag. Berlin, 1986.

3. Федер Ens. Фракталы / пер.с англ. – М.: Мир, 1991.