Àâòîðû: Manish Mehta, Rakesh Agrawal, Jorma Rissanen
Èñòî÷íèê: http://www.springerlink.com/content/mt27q3g813631k79/
SLIQ: A Fast Scalable Classifier for Data Mining
Abstract. Classification is an important problem in the emerging field of data mining. Although classification has been studied extensively in the past, most of the classification algorithms are designed only for memory-resident data, thus limiting their suitability for data mining large data sets. This paper discusses issues in building a scalable classifier and presents the design of SLIQ, a new classifier. SLIQ is a decision tree classifier that can handle both numeric and categorical attributes. It uses a novel pre-sorting technique in the tree-growth phase. This sorting procedure is integrated with a breadth-fist tree growing strategy to enable classification of disk-resident datasets. SLIQ also uses a new tree-pruning algorithm that is inexpensive, and results in compact and accurate trees. The combination of these techniques enables SLIQ to scale for lerge data sets and classify data sets irrespective of the number of classes, attributes, and examples (records), thus making it an attractive tool for data mining.
1 Introduction
The success of computerized data management has resulted in the accumulation of huge amounts of data in several organizations. There is a growing perception that analyses of these large data bases can turn this "passive data" into useful "actionable information". The recent emergence of Data Mining, or Knowledge Discovery in Databases, is a testimony to this trend. Data mining involves the development of tools that can extract patterns from large data bases.
Classification is an important data mining problem [1] and can be described as follows. The input data, also called the training set, consists of multiple examples (records), each having multiple attributes or features. Additionally, each example is tagged with a special class label. The objective of classification is to analyze the input data and to develop an accurate description or model for each class using the features present in the data. The class descriptions are used to classify future test data for which the class labels are unknown. They can also be used to develop a better understanding of each class in the data. Applications of classification include credit approval, target marketing, medical diagnosis, treatment effectiveness, store location, etc.
Classification has been studied extensively (see [13] for an excellent overview of various techniques). However, the existing classification algorithms have the, problem that they do not scale. Most of the current algorithms have the restriction that the training data should fit in memory. This is perhaps a result of the type of applications to which classification has been hitherto applied. In many applications, there were simply not many training examples available. As a matter of fact, the largest dataset in the Irvine Machine Learning repositary is only 700KB with 20000 examples. Even in [5], a classifier built with database considerations, the size of the training set was overlooked. Instead, the focus was on building a classifier that can use database indices to improve the retrieval efficiency while classifying test data.
In data mining applications, very large training sets with several million examples are common. Our primary motivation in this work is to design a classifier that scales well and can handle training data of this magnitude. The ability to classify larger training data can also improve the classification accuracy [2] [3].
Given our goal of classifying large data seta, we focus mainly on decision tree classifiers [4] [10]. Decision tree classifiers are relatively fast compared to other classification methods. Methods like neural networks can have extremely long training times even for small datasets. A decision tree can be converted into simple and easy to understand classification rules [10]. They can also be converted into SQL queries for accessing databases [5]. Finally, tree classifiers obtain similar and sometimes better accuracy when compared with other classification methods [7], Figure 1 gives an example of a decision tree classifier for a toy dataset of six examples.
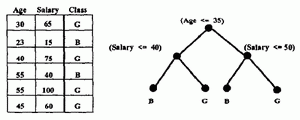
Fig. 1. Example of a decision tree
The idea of modifying tree classifiers to enable them to classify large datasets has been explored previously. Previous proposal include sampling of data at each decision tree node [2], and discretization of numeric attributes [2]. These methods decrease classification time significantly but also reduce the classification accuracy. Chan and Stolfo [3] have studied the method of partitioning the input data and then building a classifier for each partition. The outputs of the multiple classifiers are then combined to get the final classification. Their results show that classification using multiple classifiers never achieves the accuracy of a single classifier that can classify all of the data.
The decision-tree classifier we present, called SLIQ, uses novel techniques that improve learning time for the classifier without loss in accuracy. At the same time, these techniques allows classification to be performed on large disk-resident training data. Consequently, given training data that can be handled by other decision tree classifiers, SLIQ exhibits the same accuracy characteristics, but executes faster and produces small trees. However, SLIQ imposes no restrictions on the amount of training data or the number of attributes in the examples. Therefore, SLIQ can potentially obtain higher accuracies by classifying larger training datasets which cannot be handled by other classifiers.
The rest of the paper is organized as follows. Section 2 describes a genetic decision tree classifier and Section 3 discusses scalability issues. Sections 4 and 5 present the design and a detailed performance analysis of SLIQ, respectively. Finallv. Section 6 contains our conclusions.
2 Decision-Tree Classification
Most decision-tree classifiers (e.g. CART [4], C4.5 [10]) perform classification in two phases: Tree Building and Tree Pruning.
Tree Building An initial decision tree is grown in this phase by repeatedly partitioning the training data. The training set is split into two or more partitions using an attribute2. This process is repeated recursively until all the examples in each partition belong to one class. Figure 2 gives an overview of the process.
MakeTree (Training Data T)
Partition (T);
Partition (Data S)
If (all points in S are in the same class) then return;
Evaluate splits for each attribute A
Use best split found to partition S into S1 and S2;
Partition (S1):
Partition (S2);
Fig. 2. Tree-Building Algorithm
Tree Pruning The tree built in the first phase completely classifies the training data set. This implies that branches are created in the tree even for spurious “noise” data and statistical fluctuations. These branches can lead to errors when classifying test data. Tree pruning is aimed at removing these branches from the decision tree by selecting the subtree with the least estimated error rate.
3 Scalability Issues
3.1 Tree Building
There are two main operations during tree building: i) evaluation of splits for each attribute and the selection of the best split and ii) creation of partitions using the best split. Having determined the overall best split, partitions can be created by a simple application of the splitting criterion to the data. The complexity lies in determining the best split for each attribute. The choice of the splitting criterion depends on the domain of the attribute being numeric or categorical (attributes with a finite discrete set of possible values). But let us first specify how alternative splits for an attribute are compared.
3.1.1 Splitting Index A splitting index is used to evaluate the "goodness" of the alternative splits for an attribute. Several splitting indices have been proposed in the past[13]. We use the gini index, originally proposed in [4]. If a data set T contains examples from n classes, gini(T) is defined as
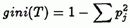
where Pj is the relative frequency of class j in T.
3.1.2 Splits for Numeric Attributes A binary split of the form A ≤ v, where v is a real number, is used for numeric attributes. The first step in evaluating splits for numeric attributes is to sort the training examples based on the values of the attribute being considered for splitting. Let v1, v2, … , vn be the sorted values of a numeric attribute A. Since any value between vi and v i+1 will divide the set into the same two subsets, we need to examine only n — 1 possible splits. Typically, the midpoint of each interval Vi — Vi+1 is chosen as the split point. The cost of evaluating splits for a numeric attribute is dominated by the cost of sorting the values. Therefore, an important scalability issue is the reduction of sorting costs for numeric attributes.
3.1.3 Splits for Categorical Attributes If S(A) is the set of possible values of a categorical attribute A, then the split test is of the form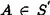 
, where 
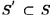. Since the number of possible subsets for an attribute with n possible values is 
, the search for the best subset can be expensive. Therefore, a fast algorithm for subset selection for a categorical attribute is essential.
3.2 Tree Pruning
The tree pruning phase examines the initial tree grown using the training data and chooses the subtree with the least estimated error rate. There are two main approaches to estimating the error rate; one using the original training dataset and the other using an independent dataset for error estimation.
Cross-validation [4] belongs to the first category. Multiple samples ate taken from the training data and a tree is grown for each sample. These multiple trees are then used to estimate the error rates of the subtrees of the original tree. Although this approach selects compact trees with high accuracies, it is inapplicable for large data sets, where building even one decision tree is expensive. Alternative approaches [10] that use only a single decision tree often lead to large decision trees.
The second class of methods divide the training data into two parts where one part is used to build the tree and the other for pruning the tree. The data used for pruning should be selected such that it captures the "true" data distribution, which brings up a potential problem with this method. How large should the test sample be and how should it be selected? Moreover, using portions of the data only for pruning, reduces the number of training examples available for the tree growing phase, which can lead to reduced accuracy.
The challenge for a scalable classifier in the pruning phase is to use an algorithm that is fast, and leads to compact and accurate decision trees.
4 SLIQ Classifier
We first give a. brief overview of SLIQ and then give details about the techniques used in SLIQ to address the scalability issues identified in the previous section.
4.1 Overview
SLIQ is a decision tree classifier that can handle both numeric and categorical attributes. SLIQ uses a pie-sorting technique in the tree-growth phase to reduce the cost of evaluating numeric attributes. This sorting procedure is integrated with a breadth-first tree growing strategy to enable SLIQ to classify disk-resident datasets. In addition, SLIQ uses a fast subsetting algorithm for determining splits for categorical attributes. SLIQ also uses a new tree-pruning algorithm based on the Minimum Description Length principle [11], This algorithm is inexpensive, and results in compact and accurate trees. The combination of these techniques enables SLIQ to scale for large data sets and classify data sets with a large number of classes, attributes, and examples.
4.2 Pre-Sorting and Breadth-First Growth
For numeric attributes, sorting time is the dominant factor when finding the best split at a decision tree node [2]. Therefore, the first technique used in SLIQ is to implement a scheme that eliminates the need to sort the data at each node of the decision tree. Instead, the training data are sorted just once for each numeric attribute at the beginning of the tree growth phase.
To achieve this pre-sorting, we use the following data structures. We create a separate list for each attribute of the training data. Additionally, a separate list, called class list, is created for the class labels attached to the examples. An entry in an attribute list has two fields: one contains an attribute value, the other an index into the class list. An entry of the class list also has two fields: one contains a class label, the other a reference to a leaf node of the decision tree. The ith entry of the class list corresponds to the ith example in the training data. Each leaf node of the decision tree represents a partition of the training data, the partition being defined by the conjunction of the predicates on the path from the node to the root. Thus, the class list can at any time identify the partition to which an example belongs. We assume that there is enough memory to keep the class list memory-resident. Attribute lists are written to disk if necessary.
Initially, the leaf reference fields of all the entries of the class list are set to point to the root of the decision tree. Then a pass is made over the training data, distributing values of the attributes for each example across all the lists. Each attribute value is also tagged with the corresponding class list index. The attribute lists for the numeric features are then sorted independently. Figure 3 illustrates the state of the data structures before and after pre-sorting.
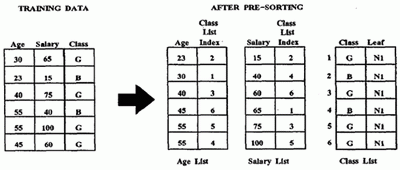
Fig. 3. Example of Pre-Sorting
EvaluateSplits ()
for each attribute A do
traverse attribute list of A
for each value v in the attribute list do
find the corresponding entry in the class list, and
hence the corresponding class and the leaf node (say L)
update the class histogram in the leaf L
If A is a numeric attribute then
compute splitting index for test (A ≤ v) for leaf L
if A is a categorical attribute then
for each leaf of the tree do
find subset of A with best split
Fig. 4. Evaluating Splits
4.2.1 Processing Node Splits Rather than using a depth-first strategy used in the earlier decision-tree classifiers, we grow trees breadth-first. Consequently, splits for all the leaves of the current tree are simultaneously evaluated in one pass over the data. Figure 4 gives a schematic of the evaluation process.
To compute the gini splitting-index (see Section 3.1) for an attribute at a node, we need the frequency distribution of class values in the data partition corresponding to the node. The distribution is accumulated in a class histogram attached with each leaf node. For a numeric attribute, the histogram is a list of pairs of the form < class, frequency >. For a categorical attribute, this histogram is a list of triples of the form < attribute value, class, frequency >.
Attribute lists are processed one at a time (recall that the attribute lists can be on disk). For each value v in the attribute list for the current attribute A, we find the corresponding entry in the class list, which yields the corresponding class and the leaf node. We now update the histogram attached with this leaf node. If A is a numeric attribute, we compute at the same time the splitting-index for the test A ≤ v for this leaf. If A is a categorical attribute, we wait till the attribute list has been completely scanned and then find the subset of A with the best split. Thus, in one traversal of an attribute list, the best split using this attribute is known for all the leaf nodes. Similarly, with one traversal of all of the attribute lists, the best overall split for all of the leaf nodes is known. The best split test is saved with each of the leaf nodes.
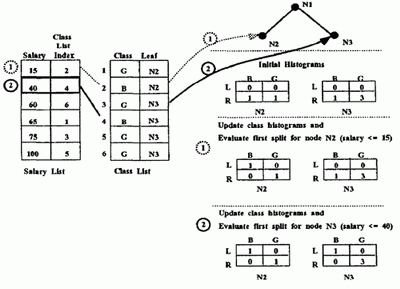
Fig. 5. Evaluating Splits: Example
Figure 5 illustrates the evaluation of splits on the salary attribute for the second level of the decision tree. The example assumes that the data has been initially split on the age attribute using the split age ≤ 35. The class histograms reflect the distribution of the points at each leaf node as a result of the split. The L values represent the distributions for examples that satisfy the test and R values represent examples that do not satisfy the test We show how the class histograms are updated as each split is evaluated. The first value in the salary list belongs to node N2. So the first split evaluated is (salary ≤ 15) for N2. After this split, the corresponding example (salary 15, class index 2) which satisfies the predicate belongs to the left branch and the rest belong to the right branch. The class histogram of node N2 is updated to reflect this fact. Next, the split (salary ≤ 40) is evaluated for node N3. After the split, the corresponding example (salary 40, class index 4) belongs to the left branch and the class histogram, of node N3 is updated to reflect this fact.
4.2.2 Updating the Class List The next step is to create child nodes for each of the leaf nodes and update the class list. Figure 6 gives the update process.
UpdateLabels ()
for each attribute A used in a split do
traverse attribute list of A
for each value v in the attribute list do
find the corresponding entry in the class list (say e)
find the new class c to which v belongs by applying
the splitting test at node referenced from e
update the class label for e to c
update node referenced in e to the child corresponding to the class c
Fig. 6. Updating Class List
As an illustration, Figure 7 shows the class list being updated after the nodes N2 and N3 have been split on the salary attribute. The salary attribute list is being traversed and the class list entry (entry 4) corresponding to the salary value of 40 is being updated. First, the leaf reference in the entry 4 of class list is used to find the node to which the example used to belong (N3 in this case). Then, the split selected at N3 is applied to find the new child to which the example belongs (N6 in this case). The leaf reference field of entry 4 in the class list is updated to reflect the new value.
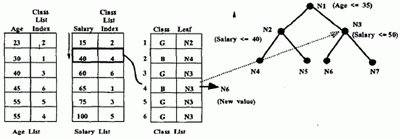
Fig. 7. Class List Update: Example
4.2.3 An Optimization While growing the tree, the above two steps of splitting nodes and updating labels are repeated until each leaf node becomes a pure node (i.e. it contains examples belonging to only one class) and no further splits are required. Note that some nodes may become pure earlier than others and it may be better to condense the attribute lists to discard entries corresponding to examples belonging to these pure nodes. This optimization can easily be implemented by rewriting condensed lists when the savings from reading smaller lists outweigh the extra cost of writing condensed lists. The information required to make this decision is available from the previous pass over the data. The important thing to note about pre-sorting and breadth-first growth is that these strategies allow SLIQ to scale for large data sets with no loss in accuracy. This is because the set of splits evaluated with and without pre-sorting is identical. Pre-sorting simply eliminates the task of resorting data at each node and removes the restriction that the training set be memory-resident.
4.3 Subset ting for Categorical Attributes
The splits for a categorical attribute A are of the form 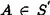, where 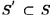and S is the set of possible values of attribute A. The evaluation of all the subsets of S can be prohibitively expensive, especially if the cardinality of S is large.
SLIQ uses a hybrid approach to overcome this issue. If the cardinality of S is less than a threshold, MAXSETSIZE, then all of the subsets of S are evaluated 3. Otherwise, a greedy algorithm (initially proposed for IND [8]) is used to obtain the desired subset. The greedy algorithm starts with an empty subset S' and adds that one element of 5 to 5 which gives the best split. The process is repeated until there is no improvement in the splits. This hybrid approach finds the optimal subset if S is small and also performs well for larger subsets.
4.4 Tree Pruning
The pruning strategy used in SLIQ is baaed on the principle of Minimum Description Length (MDL) [11]. We first review briefly the MDL principle and then show its application in decision-tree pruning.
The MDL principle states that the best model for encoding data is the one that minimiaes the sum of the cost of describing the data in terms of the model and the cost of describing the model. If M is a model that encodes the data D, the total cost of the encoding, cost(M, D), is denned as:
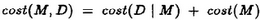
Earlier applications of the MDL principle to tree pruning [9] [12] showed that accuracy. In [6], an alternative application of MDL was presented that yielded small trees without sacrificing accuracy. However, the pruning algorithm in [6] was limited; it either pruned all or none of the children of a node in the decision tree. We present a new algorithm that is able to prune a subset of the children at each node and thus subsumes the previous algorithm.
There are two components of the pruning algorithm: the encoding scheme that determines the cost of encoding the data and the model, and the algorithm used to compare various subtrees of T.
4.4.1 Data Encoding The cost o£ encoding a training set 5 by a decision tree
T is defined as the sum of all classification errors. A classification of an example ia an error if the classification produced by T is not the same as the original class label of the example. This count of misclassificatioti errors is collected during the tree building phase. So, the data encoding step is inexpensive.
4.4.2 Model Encoding The encoding scheme for the model has to provide for the cost of describing the tree and the costs of describing the tests used in the tree at each internal node.
— Encoding the Tree: Given a decision tree, a node in the decision tree can be an internal node with one or two children, or a leaf node. The number of bits required to encode the tree depends on the permissible tree structures. We explore three possible ways of encoding the tree:
1. Code1: A node is allowed either 0 or two children. Since there are only two possibilities, it takes only one bit to encode each node.
2. Code2: Each node can have no children, a left child, a right child, or both children. Therefore, 2 bits are needed to encode the four possible values of each node.
3. Code3: Only internal nodes are examined. So each node can have a left child, a right child, or both children. This requires log(3) bits
— Encoding the Splits: The cost of encoding the splits depends on the type of attribute tested for the split:
1. Numeric Attributes: If the split is of the form A ≤ v where A is a numeric attribute and v is a real-valued number, the cost of encoding this test is simply the overhead of encoding v, say P. Although the value of P should optimally be determined independently for each such test in the decision tree, we assume a constant value of 1 throughout the tree. The value of 1 was empirically determined.
2. Categorical Attributes: For tests of the form A 
S, where A is a categorical attribute and S is a subset of the possible values of A, the cost is calculated in a two-step process. First, we count the number of such tests used in the tree,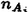 
, for each categorical attribute Ai. Then the cost of the test is calculated as Ln( ).
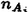From now on, 
denotes the cost of encoding any teat at an internal node.
4.4.3 Pruning Algorithms The MDL pruning evaluates the code length at prune the left or the right child, or leave the node intact. For each of the above options, the code length C(n) for a node n is calculated as follows:
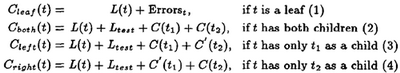
Except for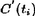 
all the other quantities are self-explanatory. In the case of partial pruning when either t1 or t2 is pruned, the examples that fall into the pruned branch are encoded using the statistics at the parent node. 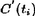represents the cost of encoding the children's examples using the parent's statistics.
We consider three pruning strategies:
1. Full: This strategy, first presented in [6], considers only options (1) and (2). If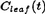 
is smaller than 
for a node t then both the children are pruned and the node is converted into a leaf. This approach codes the decision tree using only one bit (method Code1).
2. Partial: The partial pruning strategy chooses amongst all four options. Each node is converted into the option with the shortest code length. This approach uses the second method for coding trees, Code2, which requires 2 bits for each node.
3. Hybrid: The hybrid method prunes the tree in two phases. It first uses the Pull method to get a smaller tree and then considers only options (2), (3) and (4) to further prune the tree.
5 Performance Results
This section presents a detailed performance evaluation of SLIQ. We first discuss the metrics used in the evaluation and then describe the experimental methodology. This is followed by a comparison of SLIQ with other tree classification methods and the result of experiments showing SLIQ's scalability.
5.1 Metrics
The primary metric for evaluating classifier performance is classification accuracy-the percentage of test samples that are correctly classified. We also present the classification time, and the size of the decision tree as secondary metrics. The ideal goal for a classifier is to produce compact, accurate trees in a short time.
5.2 Experimental Setup
The performance evaluation of SLIQ was divided into two parts. The first part compares SLIQ with the classifiers provided with the IND classifier package [8]. The IND package implements two of the most popular decision tree classifiers: CART [4] and C4 (a predecessor of C4.5 [10]). These implementations are henceforth referred to as IND-Cart and IND-C4. Since the IND classifiers handle only datasets that fit in memory, the comparison used datasets from the STATLOG classification benchmark [7]. Table 1 summarizes the important parameters of this benchmark.
The second part of the performance evaluation examines SLIQ's performance on disk-resident data. In the absence of a benchmark with large classification datasets, we used the evaluation methodology and synthetic databases proposed in [1]. Each tuple in these databases has nine attributes. Ten classification func¬tions were used in [1] to produce data distributions of varying complexities. In this paper, we use the functions which were the hardest to characterize and led to the highest classification errors — functions 5 and 10. All experiments were
performed on an IBM RS/SOOO 250 workstation with a buffer pool of 64 MB
and executing the AIX 3.2.5 OS.
5.3 MDL Pruning
Section 4.4 presented the partial and hybrid MDL-based pruning algorithms that
can remove a subset of the children at any decision tree node. The first experiment compares the performance of these algorithms to the full pruning algorithm. Table 2 shows the classification accuracy of the different algorithms while Table 3 shows the sizes of the final decision tree. The execution times of the three algorithms nearly the same and have therefore not been shown.
The tables show that compared to full pruning, the partial pruning leads to much smaller trees but at the cost of lower classification accuracy. This implies that the partial MDL pruning is “over-aggressive”. Hybrid pruning, on the other hand, achieves the same accuracy as full pruning, and leads to decision trees that are, on the average, 22% smaller. Hybrid pruning is therefore the preferred approach, and is used for the rest of the experiments in this paper.
5.4 Small Datasets
The next experiment compares the performance of SLIQ with IND-Cart and IND-C4. Table 4 shows the classification accuracy of each of the algorithm on the STATLOG benchmark. The results show that all the three classifiers achieve similar accuracy. The largest difference is only 5.3% (Diabetes). However I Table 5
shows that there is a significant difference in the sires of the decision trees produced by the classifiers. IND-C4 produces the largest decision trees for all the datasets. The trees produced by IND-Cart are 2 (Segment) to 16.4 (Australian) times smaller. SLIQ also produces trees that are comparable in size to IND-Cart and 2.1 (Shuttle) to 8.5 (Diabetes) times smaller than IND-C4.
The final criterion for comparing the pruning algorithms is the execution times of the algorithms. Table 6 shows that IND-Cart, which uses cross-validation for pruning, has the largest execution time. The other two algorithms grow a single decision tree, and therefore are nearly an order of magnitude faster in comparison. SLIQ is faster than IND-C4, except for the Australian, Diabetes, and DNA data. The Australian and Diabetes data are very small and, therefore, the full potential of pre-sorting and breadth-first growth cannot be fully exploited by SLIQ. The DNA data consists only of categorical attributes, and hence there are no sorting costs that SLIQ can reduce.
In summary, this set of experiments has shown that IND-Cart achieves good accuracy and small trees. However, the algorithm is nearly an order of magnitude slower than the other algorithms. IND-C4 is also accurate and has fast execution times, but leads to large decision trees. SLIQ, on the other hand, does not
suffer from any of these drawbacks. It produces accurate decision trees that are significantly smaller than the trees produced using IND-C4. At the same time, SLIQ executes nearly an order of magnitude faster than IND-Cart.
5.5 Scalability
The last set of experiments showed that SLIQ achieves good performance on memory-resident data. This section examines the scalability of SLIQ along two dimensions: the number of training examples, and the number of attributes in the data. Synthetic databases (Section 5.2) were used for these experiments.
Scalability on number of training examples Figure 8 shows the performance of SLIQ as the number of training examples is increased from 100,000 to 10 million. This corresponds to an increase in total database size from 4MB to 400MB.
The results show that SLIQ achieves near-linear execution times on disk-resident data. This is because the total classification time is dominated by I/O costs. Recall that SLIQ makes at most two complete passes over the data for each level of the decision tree. Since I/O costs are directly proportional to the
size of the data, the total classification time also becomes a near-linear function of data size. The two functions show different slopes because the size of the tree and hence the number of passes made over the data is function-dependent. Total linearity is not achieved because of two reasons. First, the pre-sorting time is non-linear in the size of the data. Second, classifying larger data sets sometimes
leads to larger decision trees which requires extra passes over the data.
Scalability on number of attributes The next experiment studies the performance of SLIQ as the number of attributes increases. Since the original synthetic databases have only 9 attributes, extra attributes were created by adding randomly generated values to each example. Note that the addition of these attributes does not substantially change the final decision tree produced because the extra attributes are not used by SLIQ anyway. The additional attributes simply increase the classification time because of the need to examine additional attributes at each level of the decision tree. The number of training examples
was fixed at 100,000 for this experiment. The number of attributes was increased from 9 to 400, which represents an increase in the database size from 4MB to 160MB. Figure 9 shows the performance for functions 5 and 10. There is a discontinuity at 100 attributes, when the database size is just over 40 MB and the attribute lists (80 MB) do not fit in memory. Recall that the buffer pool size was fixed at 64 MB of memory for all the experiments. For disk-resident data, the classification time increases linearly, again due to the domination of I/O costs.
6 Conclusions
Classification is an important problem in data mining. Although classification has been studied extensively in the past, the various techniques proposed for classification do not scale well for large data sets. We presented a new decision-tree classifier, called SLIQ, which is designed specifically for scalability. SLIQ uses the novel techniques of pre-sorting, breadth first growth, and MDL-based pruning. An empirical performance evaluation shows that compared to other classifiers, SLIQ achieves comparable or better classification accuracy but produces small decision trees and and has small execution times. We also demonstrated that SLIQ achieves good scalability and performs well for datasets with a large number of examples and attributes.
References
1. R. Agrawal, T. Imielinski, and A. Swami. Database mining: A performance per-
spective. IEEE fians. on Knowledge and Data Engineering, 5(6), Dec. 1993.
2. J. Catlett. Megainduction: Machine Learning on Very Large Databases. PhD the-
sis, University of Sydney, 1991.
3. P. K. Chan and S. J. StoIfo. Meta-learning for multistrategy and parallel learning.
In Proc. Second Intl. Workshop on Mu&strategy Learning, pages 150-165, 1993.
4. L. Breiman et. al. Classification and Regression Trees. Wadsworth, Belmont, 1984.
5. R. Agrawal et. al. An interval classifier for database mining applications. In Proc.
of the VLDB Conf., Vancouver, British Columbia, Canada, August 1992.
6. M. Mehta, J. Rissanen, and R. Agrawal. MDL-based decision tree pruning. In
Int? Conf. on Knowledge Discovery in Databases and Data Mining (KDD-95),
Montreal, Canada, Aug. 1995.
7. D. Michie, D. J. Spiegelhalter, and C. C. Taylor. Machine Learning, Neural and
Statistical Classification. E&s Horwood, 1994.
8. NASA Ames Res. Ctr. Intro. to IND Version 2.1, GA23-2475-02 edition, 1992.
9. J. R. Quinlan and R. L. Rivest. Inferring decision trees using minimum description
length principle. Information and Computation, 1989.
10. J. Ross Quinlan. C4.5: Programs for Machine Learning. Morgan Kaufman, 1993.
11. J. Rissanen. Stochastic Complexity in Statistical Inquiry. World Scientific Publ.
Co., 1989.
12. C. Wallace and J. Patrick. Coding decision trees. Machine Learning, 11:7-22,
1993.
13. S. M. Weiss and C. A. Kulikowski. Computer Systems that Learn: Classification
and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Ex-
pert Systems. Morgan Kaufman, 1991.
