Àâòîðû: A. Lendasse, J. Lee, E. de Bodt, V. Wertz, M. Verleysen
Èñòî÷íèê: http://www.dice.ucl.ac.be/~verleyse/papers/bookLesage03al.pdf
APPROXIMATION BY RADIAL BASIS FUNCTION NETWORKS
Application to Option Pricing
INTRODUCTION
The approximation of functions is one of the most general uses of artificial neural networks. The general framework of the approximation problem is the following. One supposes the existence of a relation between several input variables and one output variable. This relation being unknown, one tries to build an approximator (black box model) between
these inputs and this output. The structure of this approximator must be chosen and the approximator must be calibrated as to best represent the input-output dependence. To realize these different stages, one disposes of a set of inputs-output pairs that constitute the learning data of the
approximator.
The most common type of approximator is the linear approximator. It
has the advantage of being simple and cheap in terms of computation load,
but it is obviously not reliable if the true relation between the inputs and the
output is nonlinear. One has then rely on nonlinear approximators such as
artificial neural networks.
The most popular artificial neural networks are the multilayer
perceptrons (MLP) developed by Werbos [1] and Rumelhart [2]. In this
chapter, we will use another type of neural networks: the radial basis
function networks (or RBFN) [3]. These networks have the advantage of
being much simpler than the perceptrons while keeping the major property
of universal approximation of functions [4]. Numerous techniques have
been developed for RBFN learning. The technique that we have chosen has
been developed by Verleysen and Hlavackova [5]. This technique is
undoubtlessly one of the simplest ones but it gives very good results. The
RBFN and the learning technique chosen will be presented in section 1.
We will demonstrate that the results obtained with RBFN can be
improved by a specific pre-treatment of the inputs. This pre-treatment
technique is based on linear models. It does not complicate the RBFN
learning but yields very good results. The pre-treatment technique will be
presented in section 2.
These different techniques will be applied to option pricing. This
problem has been successfully handled by for instance Hutchinson, Andrew
and Poggio in 1994 [6], a work that has surely widely contributed to give
credibility to the use of artificial neural networks in finance. The existence
of a chapter dedicated to neural networks in the work of Lo, Cambell and
MacKinlay [7] sufficiently attests to it. Hutchinson et al., by using notably
simulated data, have demonstrated that RBFN allow to price options, and
also to form hedged portfolios. The choice that the authors made of the
determination of a call option price as application domain of neural networks
in finances is certainly not an accident. The financial derivatives assets
indeed characterize themselves by the nonlinear relation that links their
prices to the prices of the underlying assets. The results that we obtain are
comparable to those of Hutchinson et al. but with a simplified learning
process. We will demonstrate with this example the advantages of our
technique of data pre-treatment. This example will be handled in detail in
section 3.
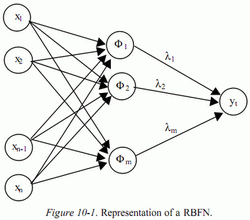
1. APPROXIMATION BY RBFN
We dispose of a set of inputs Xt and a set of outputs Yt. The
approximation of y, by a RBFN will be noted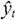 
. This approximation will be
the weighted sum of m Gaussian kernels Φ :
t = 1 to N , with
The RBFN is illustrated in figure 1.
The complexity of a RBFN is determined by the number of Gaussian
kernels. The different parameters to specify are the position of the Gaussian
kernels (Ci), their variances (σi), and the multiplicative factors (λi). The
technique that allows determining them is developed in detail in [5]. We
will explain it briefly.
The position of the Gaussian kernels is chosen according to the
distribution of Xt in space. At locations where there are few inputs Xt few
nodes will be placed and conversely, a lot of nodes will be placed where
there are many input data.
The technique that allows realizing this operation is called vector
quantization and the points that summarize the position of the nodes are
called centroids. The vector quantization is composed of two stages. The
centroids are first randomly initialized in the space. They are then placed in
the following way. All Xt points are inspected, and for each of them the
closest centroid will be moved in the direction of xt according to the
following formula:
with xt the considered point, Ci the closest centroid to Xt, and α a parameter that decreases with time. Further details on vector quantization methods can be found in [8,9].
The second parameter to be chosen is the standard deviation (or width) of
the different Gaussian kernels (σi). We chose to work with a different width
for each node. To estimate them, we define the Voronoï zone of a centroid
as the space region that is closest to this centroid than to any other centroid.
In each one of these Voronoï zones, the variance of the points belonging to
that zone is calculated. The width of a Gaussian kernel will be the product
of the variance in the Voronoï zone where the node is located, multiplied by
a factor k. We will explain in our application how to choose this parameter
[10]. This method has several advantages, the most important being that the
Gaussian kernels better cover the space of the RBFN inputs.
The last parameters to determine are the multiplicative factors λi. When
all other parameters are defined, these are determined by the solution of a
system of linear equations.
The total number of parameters equals m*(n+1)+1 with n being the
dimension of the inputs space and m being the number of Gaussian kernels
used in the RBFN.
2. RBFN WITH WEIGHTED INPUTS
One of the disadvantages of the RBFN that we have presented is that they
give an equal importance to all input variables. This is not the case with
other approximators of functions such as the MLP. We will try to eliminate
this disadvantage without penalizing the parameters estimation process of
the RBFN.
Let’s suppose first that all inputs are normalized. We understand by this that they all have zero mean and unit variance. If we build a linear model between the inputs and the output, the latter will be approximated by a weighted sum of the different inputs. The weighting associated to each input determines the importance that this latter has on the approximation of the output. Indeed, if one differentiates the linear model with respect to the different inputs, one finds back these very same weightings. This is illustrated in the following example:
which yields:
We thus dispose of a very simple mean to determine the relative importance that the different inputs have on the output. We will then multiply the different normalized inputs by the weighting factors obtained from the linear model. These new inputs will be used in a RBFN such as the one we presented in the previous section. This new RBFN that we will qualify as «weighted», will thus give a different importance to the different input variables.
3. OPTION PRICING
The initial success of neural networks in finance has most surely been
motivated by the numerous applications presented in the field of assets price
prediction (Cottrell, de Bodt and Levasseur [11] present a wide synthesis of
obtained results in this field). The emergence of nonlinear prevision tools
and their universal approximation properties, obviously not well understood,
brought in new hopes. Quickly though, it appeared that forecasting the price
of assets remains an extremely complex problem, that the concept of
financial markets informational efficiency introduced by Fama [12] is no
idle words; to overperform financial markets, after having taken account of
the transaction costs and the level of risk taken is not simple.
The application studied in this section, the modeling of the behavior of the price of a call option, as developed by Hutchinson, Lo and Poggio [6], presents a typical case of application of neural networks in finance. The prices of the derivatives depend nonlinearly on the price of the underlying assets. Major advances have been introduced in finance to set up analytical evaluation formulas for assets derivatives. The most famous is undoubtedly the one established by Black and Scholes [13], daily used nowadays by the majority of financial operators. Evaluation formulas of options prices are based on very strict assumptions among which, for example, the fact that the actions prices follow a geometric Brownian motion. The fact that these assumptions are not strictly verified in practice explains that the prices observed on financial markets deviate more or less significantly from the theoretical prices. In this context, to dispose of a universal function approximator, capable of capturing the nonlinear relation that links an option price to the price of its underlying asset, but that does not rely on the assumptions necessary for the setting up of analytic formulas, presents an obvious interest. It is though necessary that the proposed tool be reliable and robust for it to be adopted by the financial community. This is indeed our major concern.
3.1 Generating data
The RBFN with weighted inputs has been tested on an example of
determination of a call option price. This example has been handled by
Hutchinson, Lo and Poggio in 1994 [6], and we will use the same method of
generation of data.
To generate their data, the authors use in their article the Black and
Scholes formula [13] in order to simulate the call option prices. This
formula is the following:
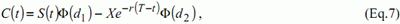
with
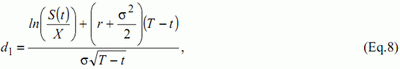
and
In the above formulas, C(t) is the option price, S(t) the stock price, X the strike price, r the risk-free interest rate, T-t the time-to-maturity, σ the volatility and Φ is the standard normal distribution function. If r and s are stable, which is the case in our simulations, the price of the call option will only be function of S(t), X and T-t. The approximation type that has been chosen is the following:
For our simulation, the prices of the option during a period of two years will be generated, in a classical way, by the following formula:
taking the number of working days by year equal to 253, and Zt a random
variable extracted from a normal distribution with µ = 0.10/253, and
variance σ2
= 0.04/253. The value S(0) equals 50 US$.
The strike price X and the time-to-maturity T-t are determined by the
rules of the «Chicago Board Options Exchange» (CBOE) [14]. In short, the
rules are the following:
1. The strike price is a multiple of 5$ for the stock prices between 25 and
200$;
2. The two closest strike prices to the stock prices are used at each
expiration of options;
3. A third strike price is used when the stock price is too close to the strike
price (less than one dollar);
4. Four expiration dates are used: the end of the current month, the end of
the next month and the end of the next two semesters.
3.2 Performance measures
Three performance measures will be used, as in Hutchinson et al. [6].
The first measure is the determination coefficient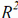 
between C et 
. The
two other performance measures are the tracking error ξ and the prediction
error η. These errors are defined as follows:
with V(t) being the portfolio value at time t, Vs the stock value, Vb the
obligations value, and Vc the option value. If the option price is correctly
evaluated, V(T) should at any time be equal to zero, given that it is a fully
hedged portfolio. The more the tracking error (ξ) deviates from 0, the more
the option price deviates thus from its theoretical value. The prediction error
is based on the classical formula of variance decomposition (the variance is
equal to the difference between the expectation of the squared variable and
its squared expectation). The expected squared V(T), in other words the
prediction average quadratic error, equals thus the sum of its squared
expectation and its variance. The terms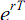 
represent the actualization terms
in continuous time, allowing the addition of obtained results at different
moments in time. A more detailed explanation of these criteria can be found
in [6].
3.3 Results
In order to measure the quality of the results obtained by classical and
weighted RBFN, we have simulated a price sample of a duration of 6 months
(using formulas (7) et (11)). Two RBFN are calibrated on these data: a
classical RBFN and a weighted RBFN. The number of Gaussian kernels is
6. This corresponds in fact to 19 parameters per RBFN, which is roughly
equivalent to the 20 parameters RBFN used in [6].
Then, one hundred test-sets are generated (using the same formulas), and
for each of the two RBFN the coefficient 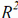is calculated. The values of ξ
and η obtained for the two RBFN and for the exact Black and Scholes
formula are also calculated.
The results obtained for 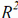(averaged on the one hundred test-sets) are
presented in Figure 4, as a function of k, the coefficient used to compute the
width of the nodes. The value of k to be used is chosen as the smallest value
giving a result (in terms of 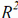) close to the asymptote, that is to say a value
that can be found in the elbow of the curves in Figure 4. The value of k = 4
has been chosen in this case.
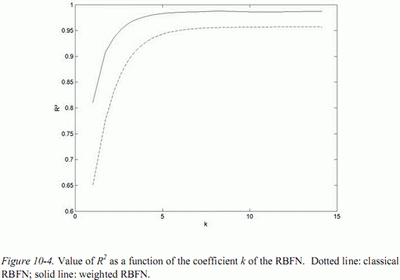
The benefit of weighting is obvious. The 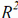obtained exceeds 97%,
which is equivalent to the results in [6] while using a RBFN with much
simpler learning process.
The results obtained for ξ and η are also in favor of the weighted RBFN.
Table 1 presents the average values and the standard deviations of , ξ and
η for both types of RBFN. As for the performance measures for the Black
and Scholes exact formula, we have ξ = 0.57 et η = 0.85.
4. CONCLUSIONS
In this paper, we have presented a simple method to parameterize a
RBFN. We have then proposed an improvement to this classical RBFN.
This improvement consists in the weighting of inputs by the coefficients
obtained through a linear model. These methods have then been tested for
the determination of the price of a call option. The results that we have
obtained show a clear advantage of the weighted RBFN whatever the
performance measure used. In addition, in the example used, the results are
comparable to the best RBFN or multilayer perceptrons that can be found in
literature. The advantages of this weighted RBFN are thus simplicity of
parameterization and quality of approximation.
ACKNOWLEDGMENTS
Michel Verleysen is Senior research associate at the Belgian Fonds
National de la Recherche Scientifique (FNRS). The work of John Lee has
been realized with the support of the Ministère de la Région wallonne, in the
framework of the Programme de Formation et d’Impulsion à la Recherche
Scientifique et Technologique. The work of A. Lendasse and V. Wertz is
supported by the Interuniversity Attraction Poles (IAP), initiated by the
Belgian Federal State, Ministry of Sciences, Technologies and Culture. The
scientific responsibility rests with the authors.
REFERENCES
[1] Werbos P. (1974), “Beyond regression: new tools for prediction and analysis in the
behavioral sciences”, PhD thesis, Harvard University.
[2] Rumelhart D., Hinton G., Williams R. (1986), “Learning representation by back-
propagating errors”, Nature 323, pp. 533-536.
[3] Powell M. (1987), “Radial basis functions for multivariable interpolation : A review”, J.C.
Mason and M.G. Cox, eds, Algorithms for Approximation, pp.143-167.
[4] Poggio T., Girosi F. (1987), “Networks for approximation and learning”, Proceedings of
IEEE 78, pp. 1481-1497.
[5] Verleysen M., Hlavackova K. (1994), “An Optimised RBF Network for Approximation of
Functions”, ESANN 1994, European Symposium on Artificial Neural Networks, Brussels
(Belgium), pp. 175-180.
[6] Hutchinson J., Lo A., Poggio T. (1994), “A Nonparametric Approach to Pricing and
Hedging Securities Via Learning Networks”, The Journal of Finance, Vol XLIX, N°3.
[7] Cambell, Y., Lo, A., MacKinlay, A. (1997), The Econometrics of Financial Markets,
Princeton University Press, Princeton.
[8] Kohonen T. (1995), “Self-organising Maps”, Springer Series in Information Sciences, Vol.
30, Springer, Berlin.
