Авторы: A. Lendasse, J. Lee, E. de Bodt, V. Wertz, M. Verleysen
Автор перевода: Стихарь А.Г.
Источник: http://www.dice.ucl.ac.be/~verleyse/papers/bookLesage03al.pdf
ПРИМЕНЕНИЕ НЕЙРОННЫХ СЕТЕЙ С РАДИАЛЬНО-БАЗИСНЫМИ ФУНКЦИЯМИ ДЛЯ РЕШЕНИЯ ЗАДАЧ АППРОКСИМАЦИИ
(перевод статьи: Стихарь А.Г., язык русский)
Введение
Аппроксимация функций является одним из самых общих использований искусственных нейронных сетей. Общая структура проблемы аппроксимации состоит в следующем: каждый предполагает существование отношения между несколькими входными переменными и одной выходной переменной. Это отношение является неизвестным, каждый пробует построить аппроксиматор (модель «черного ящика») между этими входами и этим выходом. Структура этого аппроксиматора должна быть выбрана и аппроксиматор должен быть градуирован относительно лучшего представления вход-выход. Что бы понять эти различные стадии, каждый располагает набором пар вход-выход, которые составляют обучающие данные аппроксиматора.
Самый распространенный тип аппроксиматоров – линейный аппроксима-тор. Преимущество в том, что он простой и дешевый в терминах загрузки вычислений, но он очевидно не надежный, если истинное отношение между входами и выходами не линейно. Тогда полагаются на нелинейный аппроксиматор, такой как искусственные нейронные сети.
Самые популярные искусственные нейронные сети – это многослойный персептрон (MLP), разработанный Werbos [1] и Rumelhart [2]. В этой главе, мы будем использовать другой тип нейронных сетей: радиальнобазисные нейрон-ные сети (или RBFN) [3]. Эти сети имеют преимущество, т.к. они более просты чем персептрон, сохраняя при этом главные свойства универсальных аппрок-симаторов функций [4]. Многочисленные методики были разработаны для обучения RBFN. Методика, которую мы выбрали, разработана Verleysen и Hlavackova [5]. Эта методика, несомненно, одна из самых простых, но дает очень хо-рошие результаты. RBFN, и выбранная методика обучения будут представлены в разделе 1.
Мы будем демонстрировать, что результаты, полученные с помощью RBFN, могут быть улучшены определенной предобработкой входов. Эта методика предобработки основывается на линейных моделях. Это не усложняет обучение RBFN, но дает очень хорошие результаты. Методика предобработки будет представлена в разделе 2.
Эти различные методики будут применены к оценке ценообразования. Эта проблема была успешно решена, например, Hutchinson, Andrew и Poggio в 1994 [6], работа, которая, несомненно, значительно содействовала использованию искусственных нейронных сетей в финансах. Существование главы, посвящен-ной искусственным нейронным сетям в работах Lo, Cambell и MacKinlay [7] достаточно подтвердило это. Hutchinson и другие, при использовании особенно моделируемых данных, демонстрировали, что RBFN позволяет ценовым оп-ционам сформировать застрахованные портфели. Выбор, сделанный авторами, из определения цены опциона покупателя, как прикладной области нейронных сетей в финансах, конечно не случайность. Финансовые активы производных в самом деле характеризуют себя нелинейным отношением, которое связывает их цены с ценами основных активов. Результаты, которые мы получаем, сопоста-вимы с таковыми из Hutchinson и др., но с упрощенным процессом обучения. Мы будем демонстрировать с этим примером преимущества нашей методики предобработки данных. Этот пример будет детально рассмотрен в разделе 3.
1. Аппроксимация RBFN (нейронные сети с радиально базисной функцией)
Мы избавляемся от множества входов Xt и множества выходов Yt. Значение y, аппроксимированное RBFN, будет помечено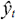 
. Эта аппроксимация будет являться взвешенной суммой по m Гауссова ядра
t = 1 .. N, с
Радиально базисная нейронная сеть проиллюстрирована на рис. 1
Сложность RBFN определена количеством Гауссовых ядер. Используются различные параметры, для определения позиции Гауссовых ядер (Ci), их дисперсий (σi), и мультипликативных факторов (λi). Методика, позволяющая их определять, подробно описана в [5]. Мы объясним это кратко.
Позиция Гауссовых ядер выбирается согласно распределению Xt в слое. В местоположениях, где немного входов Xt – будет помещено немного узлов и наоборот, много узлов будет помещено там, где есть много входных данных.
Методику, которая позволяет реализовать эту операцию – называют векторным квантованием и точки, которые суммируют позиции узлов – называют центроидами (центрами тяжести). Векторное квантование состоит из двух стадий. Вначале, центроиды в слое проинициализированы случайным образом. Затем они размещаются следующим образом. Все точки xt изучены (просмотрены), и для каждой из них ближайший центроид будет перемещен в направлении Xt, согласно следующей формуле:
Где Xt – рассматриваемая точка, Ct ближайший центроид к Xt, и α, параметр, который уменьшается со временем. Дальнейшие детали, относительно методов векторного квантования могут быть найдены в [8,9].
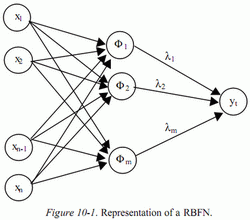
Рис. 1.1 – Представление радиально базисной нейронной сети.
Второй параметр, который будет выбран – это среднеквадратическое отклонение (или ширина), различных Гауссовых ядер (σi). Мы хотели работать с различной шириной для каждого узла. Чтобы оценить их, мы определяем зону Voronoi центроида, как область слоя, которая является самой близкой к этому центроиду, чем к любому другому центру тяжести. В каждой из этих зон Voronoi, вычислена дисперсия точек, принадлежащих той зоне. Ширина Гауссова ядра будет результатом умножения дисперсии в зоне Voronoi, где расположен узел, на фактор k. Мы объясним в нашей работе как выбрать этот параметр [10]. Этот метод имеет несколько преимуществ, наиболее важным является то, что Гауссовы ядра лучше покрывают входной слой RBFN.
Последние параметры определяют мультипликативные факторы λi. Когда все другие параметры найдены, они определяются как решение системы линейных уравнений.
Общее количество параметров равняется m*(n+1)+1, где n – измерение входного слоя и m – число Гауссовых ядер, используемых в RBFN.
2. RBFN со взвешенными входами
Один из недостатков RBFN, который мы представили – это то, что они дают равную значимость всем входным переменным. Дело обстоит не так, как с другими функциями аппроксиматорами, как например, MLP. Мы будем пытаться устранить этот недостаток, без «ущерба» процессу оценивания параметров RBFN.
Для начала, давайте полагать, что все входы нормализованы. Под этим мы понимаем, что все они имеют нулевое среднее и единичную дисперсию. Если мы построим линейную модель между входами и выходом, то последний будет аппроксимирован взвешенной суммой различных входов. Умножение на весовой коэффициент, связное с каждый входом определяет важность того, что этот последний выход будет аппроксимирован. В действительности, если вы дифференцируете линейную модель относительно входов, каждый посчитал их весьма похожими на умножение на весовой коэффициент. Это иллюстрируется следующим примером:
Которое дает:
Таким образом, мы избавляемся от очень простого среднего, что бы определить относительную значимость (влияние) различных входов на выход. Затем мы умножим разные нормализованные входы на весовые коэффициенты, полученные от линейной модели. Эти новые входы будут использоваться в RBFN, как например мы представили в предыдущей секции (разделе). Этот новый RBFN, который мы квалифицируем как «взвешенный», таким образом даст разную значимость различным входным переменным.
3 Генерация данных
RBFN со взвешенными входами был опробован на примере определения цены опциона покупателя. Этот пример был обработан Хатчинсоном, Ло и По-гджо в 1994 [6], и мы будем использовать тот же самый метод генерации данных.
Для генерации этих данных, авторы используют в их статье формулу «Бле-ка и Шольза» [13] подходящую для моделирования цены опциона покупателя. Эта формула имеет следующий вид:
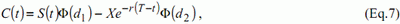
где
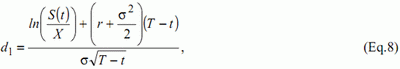
и
В вышеуказанных формулах, C(t) – это цена опциона, S(t) – курс акций, X цена страйка, r – безрисковая процентная ставка, T-t – срок погашения, σ – изменчивость и Φ – стандартная функция нормального распределения. Если r и s стабильны, что имеет место в наших моделированиях, цена на опцион покупателя будет только функцией S(t), X и T-t. Тип аппроксимации, который был выбран следующий:
Для нашей модели, цена на опцион в течение периода двух лет будет генерироваться классическим способом, по следующей формуле:
Возьмем количество рабочих дней в году равное 253, и Zt – случайная переменная, извлеченная из нормального распределения с µ = 0.10/253, и дисперсией σ2 = 0.04/253. Значение S(0) равно 50 US$.
Цена страйка Х и срока погашения T-t определена по правилам «Чикагской Биржи Опционов» (ЧБО) [14]. Короче говоря, правила имеют следующий вид:
1. Цена страйка – число кратное 5$ для курса акций между 25 и 200$;
2. Две ближайшие цены страйка к курсам акций, используются по каждому истечению срока опционов;
3. Третья цена страйка, используется когда курс акций слишком близок к цене страйка (меньше чем один доллар);
4. Используются четыре истечения срока: конец текущего месяца, конец следующего месяца и конец следующих двух семестров.
3.2 Критерии эффективности
Будут использоваться 3 критерия эффективности, как у Хатчисона и др. [6]. Первым критерием является коэффициент детерминации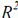 
между C и C. Два других критерия эффективности – это ошибка слежения ξ и погрешность предсказания η. Эти ошибки определены следующим образом:
Где V(t) – «портфель» величин, зависящих от t, Vs – рыночная стоимость, Vb – стоимость облигаций, и Vc – стоимость опциона. Если цена опциона правильно оценена, V(T) должно в любое время равняться 0, при условии что это полностью застрахованный портфель. Чем больше ошибка слежения (ξ) отклоняется от 0, тем больше цена опциона отклоняется от ее теоретической стоимости. Погрешность предсказания (прогноза) основывается на классической формуле декомпозиции дисперсии (дисперсия равна разнице между ожидаемым квадратом переменной и ее квадратом ожидания). Ожидаемый квадрат V(T), другими словами средняя квадратичная ошибка предсказания (прогноза), равняется т.о. сумме ее квадрата ожидания и ее дисперсии. Элементы erT представляют собой условия актуализации в непрерывное время, позволяя добавление полученных результатов в разные моменты времени. Более детальное объяснение этих критериев может быть найдено в [6].
3.3 Результаты
Для того, что бы измерять качество результатов полученных классическим и взвешенным RBFN, мы моделировали ценовой образец в течение 6 месяцев (используя формулы (7) и (11)). Два RBFN проверены на этих данных: классический RBFN и взвешенный RBFN. Число Гауссовых ядер равно 6. Это соответствует фактически 19 параметрам в RBFN, которые являются приблизительно эквивалентными 20 параметрам RBFN используемым в [6].
Затем, генерируется сто испытательных наборов (с использованием тех же самых формул), и для каждого из двух RBFN рассчитывается коэффициент 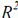. Значения ξ и η, полученные для двух RBFN и для точной формулы «Блека и Шольза» также рассчитываются.
Результаты, полученные для r 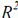(усредненные на этих ста испытательных наборах) представлены на рис. 4 как функция k, коэффициент использовался для вычисления ширины узлов. Используемое значение k выбирается как минимальное значение, дающее результат (в терминах 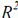)близкий к асимптоте, другими словами значение, которое может быть найдено в «колене» кривых на рис. 4. Значение k, выбранное в этом случае равно 4.
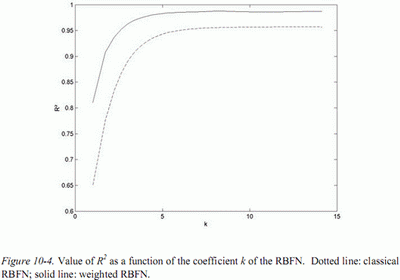
Рис 4. – Значение R2 как функции коэффициента k RBFN.
Точечная линия: классический RBFN;
сплошная линия: взвешенный RBFN.
Выгода от взвешенного RBFN является очевидной. Полученный 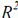превышает 97%, и является эквивалентен результатам в [6], несмотря на то, то использовался RBFN с более простым процессом обучения.
Результаты, полученные для ξ и η – так же в пользу взвешенного RBFN. Таблица 1 представляет средние значения и среднеквадратичные отклонения от 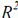, ξ и η для обоих типов RBFN. Что касается критериев эффективности для точной формулы «Блека и Шольза», мы имеем ξ = 0.57 и η = 0.85.
Таблица 1. Средние значения и среднеквадратические отклонения от от R2, ξ и η для обоих типов RBFN.
Список литературы
[1] Werbos P. (1974), “Beyond regression: new tools for prediction and analysis in the
behavioral sciences”, PhD thesis, Harvard University.
[2] Rumelhart D., Hinton G., Williams R. (1986), “Learning representation by back-
propagating errors”, Nature 323, pp. 533-536.
[3] Powell M. (1987), “Radial basis functions for multivariable interpolation : A review”, J.C.
Mason and M.G. Cox, eds, Algorithms for Approximation, pp.143-167.
[4] Poggio T., Girosi F. (1987), “Networks for approximation and learning”, Proceedings of
IEEE 78, pp. 1481-1497.
[5] Verleysen M., Hlavackova K. (1994), “An Optimised RBF Network for Approximation of
Functions”, ESANN 1994, European Symposium on Artificial Neural Networks, Brussels
(Belgium), pp. 175-180.
[6] Hutchinson J., Lo A., Poggio T. (1994), “A Nonparametric Approach to Pricing and
Hedging Securities Via Learning Networks”, The Journal of Finance, Vol XLIX, N°3.
[7] Cambell, Y., Lo, A., MacKinlay, A. (1997), The Econometrics of Financial Markets,
Princeton University Press, Princeton.
[8] Kohonen T. (1995), “Self-organising Maps”, Springer Series in Information Sciences, Vol.
30, Springer, Berlin.
