Авторы: Царегородцев В.Г.
Источник: http://www.neuropro.ru/mypapers/rostov05_3.pdf
ОПТИМИЗАЦИЯ ПРЕДОБРАБОТКИ ДАННЫХ ДЛЯ ОБУЧАЕМОЙ НЕЙРОСЕТИ:
КРИТЕРИИ ОПТИМАЛЬНОСТИ ПРЕДОБРАБОТКИ
1. Задача оптимальной предобработки выборки данных
Для искусственных нейронных сетей, обучаемых с учителем градиентными
алгоритмами на основе метода обратного распространения ошибки, скорость (время)
обучения зависит от способа предобработки значений признаков [1,2]. В [1,2] и в этой
работе рассматривается оптимизация предобработки количественных независимых
признаков (входных сигналов нейросети), поскольку для булевых и номинальных
признаков схемы предобработки однозначны, а для предобработки количественных
зависимых признаков необходимо знать возможный диапазон выходных сигналов сети.
В качестве индикатора оптимальности предобработки в [1,2] взята выборочная
оценка константы Липшица (далее КЛ). Даже при сохранении неизменными условных
энтропий между независимыми и зависимыми величинами, т.е. при линейных
масштабированиях количественных признаков, уменьшение КЛ выборки ускоряет
обучение нейросети [1,2]. Т.к. оценка КЛ требует порядка N2
вычислений расстояний
между парами примеров, в [1,2] рассмотрены способы снижения трудозатрат. Перебор
всех пар примеров выборки необходим и при поиске дублирующих (одинаковых) и
противоречивых (имеющих одинаковые вектора независимых признаков и разные
вектора зависимых признаков) примеров [3,4]. Но при оптимизации предобработки
выборки часто нужен многократный расчет КЛ, что на практике затруднительно.
Основными целями настоящей работы являются следующие:
• более широкая, по сравнению с результатами [1,2], проверка возможности
использования КЛ как индикатора оптимальности предобработки, анализ возможности
применения других или дополнительных индикаторов;
• для схем линейного масштабирования ñ выстраивание их по гипотетической степени
оптимальности и проверка действенности такого упорядочения;
• изучение возможных индикаторов оптимальности предобработки, затраты на
вычисление которых линейны по числу примеров выборки, как альтернатив КЛ.
2. Линейное масштабирование значений отдельных признаков
При линейном масштабировании можно предположить, что схема, которая
распределит предобработанные значения на наибольшем интервале, и будет лучшей,
поскольку максимальным образом (среди набора используемых схем шкалирования)
снизит выборочную КЛ. При этом вообще не требуется расчет КЛ выборки ñ можно
сравнивать интервалы значений переменных по итогам действий схем шкалирования, а
интервалы получать трансформацией только выборочных минимумов и максимумов.
Формула линейного масштабирования значения признака x для i-го примера
выборки в интервал [a,b] такова:
где Xmax, Xmin - минимальное и максимальное выборочные значения признака. Схему для интервала [-1,1] и возьмем в качестве первой рассматриваемой и базы для сравнения:
Если закон распределения признака x имеет длинные хвосты, то можно допускать
выход значений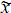 
за интервал [-1,1]: главное, чтобы новый интервал и начальная
генерация весов значений синапсов нейросети с самого начала не приводили нейроны к
насыщению, что затруднит обучение. Поэтому альтернативой (1) можно взять
масштабирование, сдвигающее выборочное среднее M(x) в 0 и помещающее ближайшее к
M(x) граничное (минимальное или максимальное) выборочное значение в -1 или 1, а
другую границу выводящее за интервал [-1,1]:
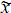по сравнению с (1) и (2) можно нормировкой 
3. Редукция исходных интервалов значений признаков для задачи классификации
Если для признака x можно упорядочить его минимальные внутри классов
значения в ряд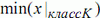 
< 
≤ ... ≤
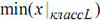, где между первыми
двумя членами выполняется строгое неравенство, то новым выборочным минимальным
значением можно взять величину 
и перед
предобработкой (по формулам (1)-(3) или иным) ограничивать диапазон значений
признака: для i-го примера брать 
что сохранит возможность разделения
классов K, L. Подобная же схема строится и для правой границы интервала значений
признака ñ для редукции максимального выборочного значения.
Фактически, это наиболее простой способ коррекции возможных выбросов в
независимых переменных. Конечно, желательно предварительно применять процедуры
коррекции выбросов, одновременно рассматривающие все множество независимых
переменных (например, [5]), как более строгие и точные, а затем выполнять редукцию
для отдельных признаков описанным способом. Далее схемы масштабирования в виде
пары "редукция - одна из формул (1)-(3)" будут соответственно названы (1р), (2р), (3р).
4. Индикаторы свойств выборок
Укажем свойства выборок, которые можно использовать наряду с оценкой КЛ или
взамен её, и затраты на оценку которых линейны по числу примеров выборки.
Геометрию "облака" данных можно описать через доли общей дисперсии,
соответствующие главным компонентам: можно оценить вытянутость эллипсоида
рассеяния в главном направлении и возможность масштабирования данных вдоль осей
эллипсоида рассеяния, а не вдоль осей координат ñ например, для декорреляции
признаков и максимизации их совместной энтропии. Но не всегда (при наличии булевых
или номинальных признаков) применение такого индикатора будет корректно.
КЛ и главные компоненты характеризуют только выборку, а взгляд на выборку со
стороны нейромодели отражают свойства матрицы Гессе целевой функции по
адаптивным параметрам нейросети, что важно, т.к. для обучения сети используются
методы градиентной оптимизации. Для оценки собственных векторов и чисел матрицы Гессе нейросети в [6] предложена итерационная процедура приближения через конечные
разности, не требующая непосредственного вычисления гессиана..
5. Экспериментальная проверка
Для экспериментов были взяты несколько баз данных из UCI KDD Database
Repository (http://kdd.ics.uci.edu/), критериями выбора являлись следующие: наличие
количественных признаков (для возможности применения формул (1)-(3)), задача
классификации с учителем (для возможности редукции исходных интервалов значений
признаков), значительная сложность задачи (число примеров в обучающей выборке).
Требование большого объема выборки основывалось на результатах [7] о сходимости с
ростом объема выборки ошибок обучения и обобщения к асимптотическому значению,
задающему предел предсказуемости (из-за шума, неинформативности признаков или
противоречивости примеров) задачи ñ чтобы не использовать никаких дополнительных
приемов повышения качества обобщения, которые могли бы повлиять на результаты.
Было взято 12 задач (12 баз данных): AnnThyroid, HypoThyroid, Letter, MUSK
Clean 2, Opt digits, Page blocks, Pen digits, Pima, Satellite, Statlog shuttle, Spambase, Yeast.
Признаки для предобработки по схемам (2), (3) выбраны эмпирически: в базах данных
взяты признаки с унимодальным неодносторонним законом распределения. Остальные
признаки предобрабатывались по схеме (1), как и отобранные признаки в стартовом
случае отсутствия специальной нормировки. Возможность же редукции интервалов
значений определялась для всех признаков.
Для каждой задачи способы предобработки были упорядочены по уменьшению
КЛ выборки. Ускорение или замедление обучения при переходе от одной предобрабоки к
другой определялось сравнением среднего по 25 сетям числа итераций обучения с
использованием метода сопряженных градиентов. Для случаев статистически
достоверного роста числа шагов обучения (несмотря на снижение КЛ выборки) было
исследовано, могли ли отличные от КЛ интегральные индикаторы оптимальности
предобработки показать причину или вероятность замедления обучения.
Общие результаты говорят, что для ускорения обучения в разы необходимо
снижать КЛ тоже в разы, а для ускорения на порядок - снижать КЛ на порядок как
сменой способа масштабирования, так и редукцией начальных интервалов значений
признаков. Рядам (1)-(2)-(3), (1р)-(2р)-(3р) предобработок соответствует снижение
времени обучения вдоль таких рядов. Исключения объясняются в следующем разделе.
Из 12-ти задач всего пять имеют тестовые выборки, для трех таких задач качество
обобщения ухудшается с уменьшением КЛ: это означает, что сложность выборок с
предобработкой снижается, сеть становится сравнительно более избыточной и может
излишне настроиться на свойства, присущие только обучающей выборке.
6. Анализ поведения индикаторов оптимальности предобработки
Снижение КЛ не всегда ускоряет обучение, но почти всем таким случаям можно
дать объяснение на основе других индикаторов оптимальности предобработки. Рост
первого собственного числа (и, вероятно, обусловленности) матрицы Гессе необученной
нейросети очень часто приводит к замедлению обучения. Увеличение же вытянутости
облака данных в главном направлении (увеличение доли дисперсии, выбираемой первой
главной компонентой) иногда не играет ухудшающей роли, но иногда приводит к
существенному ухудшению.
Т.о., результаты говорят, что и новые рассмотренные индикаторы позволяют
достаточно надежно сравнивать схемы предобработки. Но от использования КЛ
полностью отказаться все же нельзя. Можно сформировать требования к оптимальной
предобработке (и индикаторы выполнения этих требований):
1. Оптимальная схема предобработки должна минимизировать обусловленность матрицы Гессе нейросети в момент начала обучения;
2. Оптимальная предобработка должна приводить к низкой КЛ выборки как индикатору
оптимальности для завершающих шагов обучения (чем больший скачок поверхности
отклика придется аппроксимировать, тем предположительнее больше будет
обусловленность гессиана целевой функции в этой области высоких
чувствительностей выходного сигнала сети к изменению входных сигналов).
Второй пункт говорит, что только изучение нескольких пар примеров, порождающих
максимальные и близкие к ним значения КЛ, и покажет, вдоль каких направлений
(исходных переменных или главных компонент выборки) нужно масштабирование.
7. Заключение
Для оценки оптимальности предобработки обучающей выборки рассмотрено два
интегральных для выборки критерия, вычислительно менее затратные по сравнению с
ранее использовавшейся оценкой константы Липшица; экспериментально выявлена
достаточная синхронность поведения этих индикаторов и чувствительность к ухудшению
способа предобработки, иногда не идентифицируемому по оценке КЛ.
Трудность оптимизации предобработки данных обусловлена нелинейностью
обучаемой нейромодели ñ поэтому в работе сделана попытка сформировать требования к
критерию оптимальности в разные моменты процесса обучения. Именно рассмотрение
индикаторов оптимальности и, в перспективе, их динамического поведения и отличает
[1,2] и эту работу от, например, [8,9], где предлагают изменять алгоритмы обучения для
декорреляций сигналов или их центрирования, в том числе центрирования динамически
изменяющихся в процессе обучения величин невязок и сигналов нейронов скрытых слоёв
сети. Хоть центрирование сигналов и действенно [2,9], изменение алгоритмов обучения
не позволяет ни сопоставлять между собой трансформированные разными способами
выборки, ни предлагать четких советов по трансформации (предобработки) выборки или
её переменных.
Работа поддержана грантом 15G277 Красноярского краевого фонда науки.
Литература
1. Царегородцев В.Г. Предобработка обучающей выборки, выборочная константа Липшица и
свойства обученных нейронных сетей // Материалы Х Всеросс. семин. "Нейроинформатика и
ее приложения", Красноярск, 2002. 185с. - С.146-150.
2. Царегородцев В.Г. Оптимизация предобработки данных: константа Липшица обучающей
выборки и свойства обученных нейронных сетей // Нейрокомпьютеры: разработка,
применение. 2003, №7. - С.3-8.
3. Tuv E., Refenes A.N. Removal of catastrofic noise in hetero-associative training samples / Proc.
IJCNN, Nagoya, Japan, 1993. Vol.3. - pp.2628-2633.
4. Крисилов Р.А., Тарасенко В.А. Предварительная оценка качества обучающей выборки для
нейронных сетей в задачах прогнозирования временных рядов / Тр. Одес. Политехн. Ун-та.
Одесса, 2001. - Вып.1. - С.90-93.
5. Hamalainen J.J., Jarvimaki I. Input projection method for safe use of neural networks based on
process data / Proc. IJCNN, Anchorage, Alaska, USA, 1998. - pp.193-198.
6. LeCun Y., Simard P.Y., Pearmutter B. Automatic learning rate maximization by on-line estimation
of the Hessian's eigenvectors / Advances in Neural Information Processing Systems 5 (1992).
Morgan Kaufmann, 1993. - pp.156-163.
7. Cortes C., Jackel L.D., Solla S.A., Vapnik V., Denker J.S. Learning curves: Asymptotic values and
rate of convergence / Advances in Neural Information Processing Systems 6 (1993). Morgan
Kaufmann, 1994. - pp.327-334.
8. PÈrez-Ilzarbe M.J. Preconditioning method to accelerate neural networks gradient training algorithms
/ Proc. IJCNN, Washington, DC, USA, 1999. - 5p.
9. Schraudolph N.N. Centering neural network gradient factors / Neural networks: Tricks of the trade.
Springer Verlag. Lecture Notes in Comp. Sci., Vol.1524. 1998. - pp.207-226.
