В. Г. Матвейкин ИСПОЛЬЗОВАНИЕ БАЙЕСОВСКОГО ПОДХОДА В ОБУЧЕНИИ НЕЙРОННЫХ СЕТЕЙ

Авторы: В. Г. Матвейкин, С. В. Фролов
Источник: http://www.techno.edu.ru:16001/db/msg/27152.html

ИСПОЛЬЗОВАНИЕ БАЙЕСОВСКОГО ПОДХОДА
В ОБУЧЕНИИ НЕЙРОННЫХ СЕТЕЙ

Показывается, что альтернативой структурной оптимизации нейронных сетей при их обучении является использование байесовских методов регуляризации. Рассматриваются алгоритмы обучения нейронных сетей с использованием традиционных и байесовских методов регуляризации. Приводится основанный на байесовском подходе алгоритм вычисления погрешности прогноза выходных значений нейронной сети.

Одним из важнейших направлений информатизации является создание и внедрение средств вычислительной техники для автоматизации технологических процессов в промышленном производстве, на транспорте, в сельском хозяйстве и т. д. Современные системы управления строятся на базе программно-технических комплексов (ПТК) [1], которые характеризуются распределенной структурой, наличием процессоров большой вычислительной мощности, возможностью вести сбор, архивирование и хранение текущей информации от объекта. Для решения задач прогноза и оптимизации актуальным является построение экспериментальных математических моделей (ЭММ) технологических процессов на основе накопленной в архивах ПТК информации. Под ЭММ понимается оператор 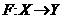, обеспечивающий отображение входного вектора x = (х₁, х₂, ..., x_n) в выходной вектор y = (y₁, y₂, ..., у_n), где 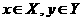Определение структуры и параметров ЭММ проводится на основе обучающей выборки. 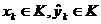Обучающая выборка характеризуется парами векторов , где — соответственно входные и выходные экспериментальные значения; .

Наиболее часто в качестве ЭММ применяются регрессионные модели [2]. Однако, как показано в [2, 3], аппроксимация функциональной зависимости степенными многочленами, используемыми в регрессионном анализе [2], применима для малой размерности n вектора входных параметров x. С ростом n резко возрастает число корректируемых параметров многочлена "проклятие размерностей" [4]), и необходима обучающая выборка экспериментальных данных большого объема. Например, для аппроксимации зависимости, имеющей 30 входных переменных, требуется степенной многочлен, содержащий примерно 46 000 корректируемых параметров [3].

Эффективным математическим аппаратом для обработки "исторических" данных о процессе являются искусственные нейронные сети (Neural Networks (NN)), которые названы и строятся по аналогии с биологическими нейронными сетями. Нейронные сети решают проблему представления нелинейного отображения у = у(x, w), форма которого управляется вектором весов w.

К одной из самых популярных архитектур NN, эффективно решающих проблему аппроксимации, относится многослойный перцептрон (Multilayer Perceptron (MLP)) (рис. 1) [5]. Сеть MLP характеризуется числом слоев сети L и числом нейронов N_l в каждом l-м слое. Связи между нейронами в каждом слое отсутствуют. Каждый i-й нейрон l-го слоя преобразует входной вектор в выходную скалярную величину . На первом этапе вычисляется функция

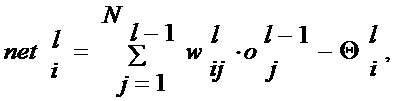(1)

где — весовой коэффициент, являющийся настраиваемым параметром и характеризующий связь j-го нейрона l — 1 -го слоя с i-м нейроном l-го слоя; — пороговый элемент.

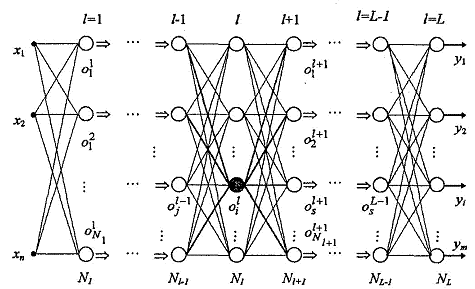
Рис.1. Структура сети MLP

Принимая , уравнение (1) перепишем в виде

(2)

Далее функция (2) преобразуется в выходную величину

(3)

Нелинейное преобразование (3) задается функцией активации, которая часто определяется сигмоидальной функцией

Имеется также много примеров прикладных исследований [5], в которых функция активации имеет простую линейную форму: .

Обучение NN на основе метода обратного распространения ошибки

Обучением NN в общем случае называется процесс изменения ее структуры и значения параметров. Когда структура и параметры сети изменяются на основе обучающей выборки , то такое обучение называется контролируемым (с учителем) [5]. Если в этом процессе используется только набор входных данных x₁, x₂,…, x_k,…, x_K, то обучение называется неконтролируемым (без учителя). Обучение сети MLP является только контролируемым. Применительно к MLP выбор структуры означает задание L и N_l . На практике эти параметры задаются априори, а процесс обучения сводится только к нахождению .

С учетом того, что в основе обучающей выборки лежат экспериментальные данные, являющиеся случайными величинами, критерий аппроксимации имеет вероятностный смысл и определяется из условия максимального правдоподобия. Для реальных объектов управления на основании многочисленных экспериментальных исследований можно предположить, что компоненте вектора соответствует условная плотность вероятности, описываемая нормальным законом распределения:

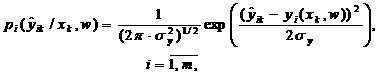
где — детерминированная функция, значение которой в точке x_k соответствует математическому ожиданию случайной величины ; — среднее квадратичное отклонение случайной величины . Тогда пара из обучающей выборки характеризуется условной плотностью вероятности:

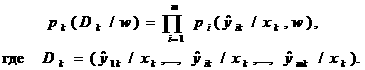
Полная плотность вероятности для обучающей выборки

или

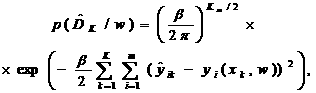(4)

где

(5)

Максимизация критерия аппроксимации (4) эквивалентна минимизации его отрицательного логарифма. Тогда критерий записывается в виде

или с учетом (4)

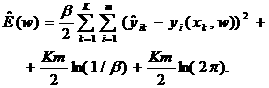(6)

Исключая из (6) множитель β и слагаемые, которые не зависят от варьируемого вектора w, для критерия максимального правдоподобия окончательно получим:

(7)

где соответствует i-му выходу сети .

Вектор веса w_ML, который вычисляется как , получил название вектора максимального правдоподобия (maximum likelihood) [6].

Таким образом, сеть MLP определяет уравнение множественной нелинейной регрессии, в которой искомыми параметрами являются компоненты вектора весовых коэффициентов w. В ряде работ, например [7—9], доказывается способность сети MLP с одним внутренним слоем и достаточно большим числом нейронов в этом слое аппроксимировать с требуемой точностью любое непрерывное отображение.

В основе методов обучения MLP лежит метод обратного распределения ошибки (error back propagation method, далее ВР) [10]. Ввиду недостаточно полного изложения в отечественной литературе, а также чрезвычайной важности метода ВР в общей теории NN приведем краткий его вывод.

Поиск оптимальных весовых коэффициентов w, при которых критерий (7) минимален, может проводиться с помощью известных методов нелинейной оптимизации [11]. Производная критерия (7) может определяться как

(8)

где e_k в теории NN принято называть мгновенной ошибкой:

(9)

По правилу дифференцирования сложной функции

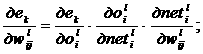(10)

Согласно (2) и (3) можно записать:

(11)

(12)

Пусть

(13)

Тогда с учетом (10) и (11) получим:

(14)

Согласно правилу дифференцирования сложной функции имеет место равенство (см. рис. 1):

(15)

С учетом (13) и того, что равенство (15) перепишем в виде

(16)

Уравнение (10) с учетом (11), (12), (16) имеет вид:

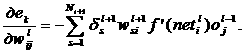(17)

Из уравнения (14) и (17) следует рекуррентная зависимость

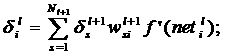(18)

Уравнение (9) согласно (2) и (3) переписывается в виде

тогда

С учетом (14) и равенства , получаем:

(19)

Таким образом, для определения производных (8) для каждой пары из обучаемой выборки вычисляются производные и выходы (фаза прямого распространения). Далее для каждого по формулам (8), (14), (18), (19) определяется производная ошибки аппроксимации (фаза обратного распространения). Исключительная вычислительная эффективность ВР достигается за счет того, что при расчете в обратном направлении используются значения и , вычисленные в фазе прямого распространения и хранимые в оперативной памяти компьютера.

В [3] показано, что при традиционном численном вычислении производных (8) требуются затраты машинного времени: , где τ — время вычисления производной; V — число весовых коэффициентов, а с применением ВР время вычисления уменьшается: τ ~ V. Использование алгоритма ВР для определения производной (8) дает возможность применять для корректировки весов на (t + 1)-м шаге известные методы нелинейной оптимизации [11]. Простейший из них — градиентный метод:

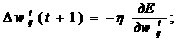(20)

где η — настроечный параметр (0 < η ≤ 1).

Для повышения сходимости алгоритма приращение в (20) может вычисляться с учетом коррекции на t-м шаге:

(21)

где — настроечный параметр (0 < ≤ 1).

Однако при использовании градиентного метода в соответствии с формулами (20), (21) наблюдается низкая скорость сходимости. К одним из самых эффективных и одновременно простых методов обучения MLP принадлежат алгоритмы Quick-prop[12] RPROP [13, 14]. Алгоритм Quick prop основан на квадратичной аппроксимации функции. Приращение веса на (t + 1)-м шаге

Основной принцип RPROP заключается в том, что приращение веса определяется только знаком производной ошибки (7) и не зависит от значения этой производной.

Методы регуляризации при обучении NN

В работе [3] показывается, что от числа степеней свободы NN — весовых коэффициентов — зависит точность аппроксимации экспериментальных данных. Сеть с недостаточным числом нейронов не может с заданной точностью представить зависимость. Избыточная структура NN также ведет к увеличению погрешности аппроксимации. При избыточной структуре NN наблюдается высокая точность аппроксимации в экспериментальных точках и одновременно большая ошибка в промежуточных точках. Это явление получило в литературе название overfitting [3,6]. При использовании методов, основанных на выборе оптимальной архитектуры NN (см., например, [15]), не устраняется возможность попадания в локальные минимумы функции ошибки (7). К тому же оптимизация по дискретным параметрам — числу нейронов — менее эффективна в вычислительном отношении, чем по непрерывным.

При обучении NN предпочтительно использовать метод регуляризации [3, 16], позволяющий определять такой вектор весовых коэффициентов w, при котором зависимость имеет более гладкий вид.

Поиск весовых коэффициентов ведется в NN с заранее выбранной избыточной структурой. Критерий (7) переписывается в виде

(22)

где — параметр регуляризации; — равномерно выпуклая функция:

(23)

в которой V — число весовых коэффициентов.

Для MLP выражение (23) имеет вид

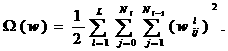
Оптимальное значение λ, может находиться итерационно [3, 16]. На (s + 1)-м шаге для каждого определяется оптимальный вектор w*, доставляющий минимум критерию (22). Поиск заканчивается, когда параметр достигает оптимума:

Более общими являются методы регуляризации, основанные на байесовском подходе [3, 6]. На основании теоремы Байеса [17] для условной плотности вероятности, описывающей распределение вектора веса w, можно записать:

(24)

где — апостериорная плотность вероятности, определяемая по (4); — плотность вероятности, являющаяся константой; p(w) — априорная плотность вероятности:

(25)

Плотность вероятности p(w) соответствует априорному предположению о том, что наиболее вероятными являются малые значения весовых коэффициентов.

Наиболее вероятный вектор весовых коэффициентов w_MP (most probable) достигается, когда . Максимизация критерия (24) эквивалентна минимизации его отрицательного логарифма. После подстановки (4), (25) в (24) и очевидных преобразований, аналогичных проведенным для критерия (4), для критерия аппроксимации окончательно получим:

(26)

где E(w) и определяются соответственно по формулам (7), (23).

Для определения оптимальных α, β проводятся следующие преобразования. Согласно [3, 6] можно записать

или с учетом (4), (25), (26)

(27)

Аналитически вычислить интеграл (27) не представляется возможным, поэтому используется методика аппроксимации подынтегрального выражения [6]. Функция (27) разлагается в точке w_MP в ряд Тейлора. С учетом предположения о том, что первая производная функции (26) в точке равна нулю, получим

(28)

где ; A — матрица Гессе размером , каждый элемент которой определяется формулой

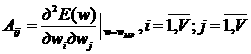(29)

Из (23), (26), (29) следует очевидное равенство

(30)

где I — единичная матрица; В — матрица вторых производных, каждый элемент которой определяется выражением

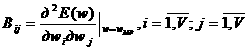
Согласно известной зависимости [6] имеет место равенство

(31)

С учетом (26)—(28), (31) после проведения очевидных преобразований получим выражение для отрицательного логарифма — :

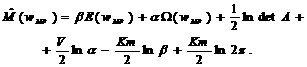(32)

Наиболее вероятные значения α, β достигаются когда

С учетом (30) и известного соотношения [6]

где Q — любая квадратная матрица; tr — оператор следа матрицы [17], получим

(33)

Если с учетом (33) продифференцировать (32) по а и р и приравнять полученные выражения к нулю, то окончательно получим:

(34)

(35)

Таким образом, алгоритм обучения NN с использованием байесовского подхода состоит из следующих шагов.

Шаг 1. s =1. Задание начальных параметров регуляризации и вектора весов w₀(s) = w₀.

Шаг 2. Минимизация критерия (26) и определения вектора w_MP.

Шаг 3. Вычисление по формулам (34), (35).

Шаг 4. Если значения α и β на предыдущем и последующем шагах мало различаются, то обучение NN закончено, иначе w₀(s+1) = w_MP, s = s + 1 и переход на Шаг 2.

Вычисление ошибки прогноза выходных значений NN

При применении NN необходимо знать, с какой погрешностью вычисляется составляющая y_i_,_K₊₁ вектора y_K₊₁ в зависимости от нового входного вектора x_K₊₁, не входящего в обучающую выборку. Выходной вектор может быть вычислен по NN, обученной на выборке . Для этого проводятся следующие преобразования. Имеет место равенство [3 ,6]:

(36)

После очевидных преобразований на основе (4), (24), (25), (27), (28), (31) получаем

(37)

Паре будет соответствовать плотность вероятности

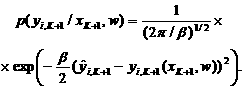(38)

Тогда (36) с учетом (37), (38) преобразуется к виду:

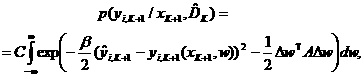(39)

где

Функция y_i_,_K₊₁(x, w) в точке (x_K₊₁, w_MP) разлагается в ряд Тейлора:

(40)

где a^T — вектор, элементы которого определяются формулой

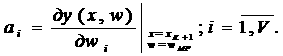(41)

После очевидных преобразований формула (39) с учетом (40), (41) принимает вид:

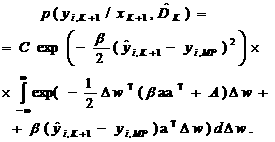(42)

С учетом известной зависимости [3] можно записать:

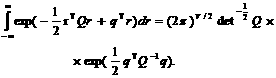
Принимая , формулу (42) перепишем в виде:

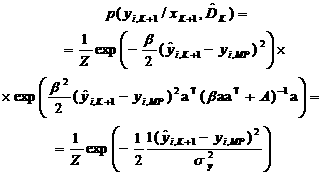(43)

где

(44)

(45)

Числитель и знаменатель формулы (44) умножаются на выражение . Учитывая, что и используя правило комбинирования матриц [17], после очевидных преобразований получим:

или

(46)

Уравнение (45) преобразуется к виду

(47)

Для собственного значения и матрицы (R + I) согласно [17] можно записать:

u(R + I) = u(R) + I. (48)

С учетом правила комбинирования матриц [17] имеют место равенства:

aa^TA^-1a = a^T A^-1aa и Ra = ua,

где а и и =а^T А^-1а — соответственно собственный вектор и собственное значение матрицы R. Тогда согласно [17] и (48), det(R + I) = u + 1 или det(βaa^T A^-1 + I) = β а А^-1а + 1.

С учетом последнего выражения, а также (5), (46), (47) можно записать:

(49)

Тогда плотность вероятности (36) с учетом (43), (49) окончательно принимает вид:

(50)

Таким образом, уравнение (50) подтверждает, что выражение (46) определяет ошибку прогноза вычисления выходного значения y_i_,_K₊₁ NN по входному вектору x_K₊₁ не входящего в обучающую выборку. Возможность определения ошибки (46) является существенным преимуществом использования байесовского подхода при обучении NN по сравнению с другими итерационными методами регуляризации, например [16].

Обучение NN типа RBF

К другой разновидности NN, позволяющей эффективно решать задачи аппроксимации экспериментальных данных, относятся NN типа RBF (Radial Basis Functions) (рис. 2) [5]. Сеть RBF состоит из одного скрытого уровня нейронов и определяется зависимостью

(51)

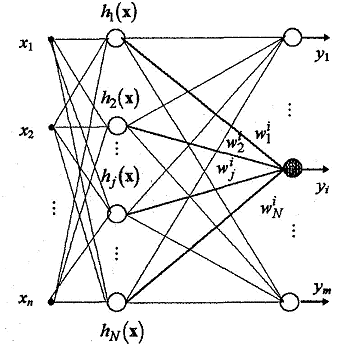
Рис. 2. Структура сети RBF

Функции базиса h_j(x), как правило, задаются в виде гауссовой функции:

(52)

где .

Для упрощения записи индекс i (формула (51)) в дальнейших выкладках опускается.

В ряде работ доказывается, что сеть RBF, так же как и MLP, является универсальным аппроксиматором [18, 19]. Обучение сети RBF в отличие от MLP состоит из двух этапов [3]. На первом этапе осуществляется неконтролируемое обучение. Для этого на регулярной сетке пространства входа X случайным образом выбирается N центров: , которые образуют классы . В качестве центров могут служить случайно выбранные входные векторы x_k из обучающей выборки. В результате классификации в каждом классе Су должно оказаться по N_j входных векторов из обучающей выборки:

(53)

где — евклидова норма.

После операции классификации (53) параметры функции (52) определяются выражениями

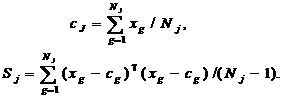
На втором этапе проводится контролируемое обучение, позволяющее определить оптимальные параметры . Критерий оптимизации имеет вид (22). Производная функции (22) по параметрам w_j

С учетом и получаем

(54)

где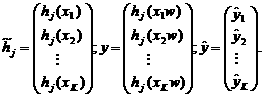

Уравнение (54) для переписывается в виде

(55)

где элемент матрицы H

С учетом (51) можно записать:

где

Для вектора y верно равенство

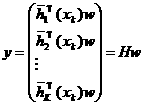Тогда из (55) определяется вектор оптимальных весовых коэффициентов:

(56)

Параметр регуляризации λ находится аналогично, как и для сети MLP итерационными методами [16]. При λ = 0 уравнение (56) переписывается в виде

где вектор w* является вектором максимального правдоподобия w* = w_MP.

При использовании байесовского подхода [6] для обучения сети RBF критерий аппроксимации (26) переписывается в виде

(57)

Тогда матрица Гессе с элементами (29), (30)

(58)

При проведении преобразований, аналогичных (54)—(56), с учетом (57), (58) для наиболее вероятного вектора весовых коэффициентов получаем равенство

Параметры α и β определяются итерационно по формулам (34) и (35), ошибка (48) переписывается с учетом (41), (51) в виде:

В отличие от сети MLP обучение сети RBF не требует применения сложных алгоритмов нелинейной оптимизации и основано на методах линейной алгебры.

Таким образом, применение байесовского подхода при обучении NN типа MNL и RBF позволяет применять эффективные алгоритмы поиска параметров регуляризации и одновременно определять погрешность прогноза выходных параметров NN.

Рис. 3. Аппроксимация экспериментальной зависимости с применением нейронной сети

В качестве примера на рис. 3 показаны результаты численных расчетов, полученных при обучении NN. Была взята обучающая выборка, состоящая из экспериментальных точек, которые расположены на равном расстоянии друг от друга по оси X и получены путем наложения на базовую функцию гауссовского шума. Для аппроксимации экспериментальной зависимости использовалась NN типа MLP с одним внутреннем слоем, который состоит из 150 нейронов, имеющих линейную функцию активации . Результаты численных исследований показывают, что при обучении NN на основе критерия (7) наблюдается описанное выше в статье явление overfitting [3, 6]. В случае применения метода регуляризации на основе байесовского подхода отображение , которое реализует NN, имеет более гладкий вид, и наблюдается более низкая погрешность в промежуточных точках.

Список литературы

1. Корнеева А. И., Матвейкин В. Г., Фролов С. В. Программно-технические комплексы, контроллеры и SCADA-сис-темы. М.: ЦНИИТЭнефтехим, 1996, 220 с.

2. Налимов В. В., Чернова Н. А. Статистические методы планирования экстремальных экспериментов. М.: Наука, 1965, 340 с.

3. Bishop С. М. Neural Networks for Pattern Recognition. Oxford: Oxford University Press, 1995, 504 p.

4. Bellman R. Adaptive Control Processes: A Guided Tour. New Jersey: Princeton University Press, 1961.

5. Jain A., Mao J., Mohiuddin K. Artificial Neural Networks: A Tutorial // Computer. 1996. № 3. P. 31-44.

6. MacKay D. J. С Bayesian interpolation // Neural Computation. 1992. V. 4, № 3. P. 415-447.

7. Hornik K., Stinchcombe M., and White H. Multilayer feedforward networks are universal approximators // Neural Networks. 1989. V.2, № 5. P. 359 - 366.

8. Kreinovich, V. Y. Arbitrary nonlinearity is sufficient to represent all functions by neural networks: a theorem // Neural Networks. 1991. V.4, № 3. P. 381-383.

9. Кафаров В. В., Гордеев Л. С, Глебов М. Б., Цэнибяо Го. К вопросу моделирования и управления непрерывными технологическими процессами с помощью нейронных сетей // ТОХТ. 1995. Т. 29, № 2. С. 205-212.

10. Rumelhart D. E., Hinton G. E., and Williams R. J. Learning internal representations by error propagation. In Rumelhart D. E. and McClelland J. L., eds. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. V. 1. P. 318—362. Cambridge. 1986. MA: The MIT Press.

11. Реклейтис Г., Рейвиндран А., Рэгсдел К. Оптимизация в технике: В 2-х кн. М.: Мир, 1986.

12. Fahlman Scott E. Faster-learning variations on back-propagation: An empirical study. In T. J. Sejnowski, G. E. Hinton and D. S. Touretzky, editors, 1988 Connectionist Models Summer School, San Mateo, CA, 1988: Morgan Kaufmann.

13. Riedmilller M. and Braun H. A direct adaptive method for faster backpropagation learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks 1993 (ICNN 93), 1993.

14. Умнов Н. А., Орлов С. Н. Сравнение алгоритмов RPROP и SCG обучения многослойных нейронных сетей // Изв. вузов. Приборостроение. 1996. Т. 39, № 1. С. 17—22.

15. Smolensky P. Mozer M. Skeletonization: A Technique for Trimming the Fat from a Network via Relevance Assessment. In D. S. Touretzky, editor, Advances in Neural Information Processing Systems (NIPS) 1. P. 107—115, San Mateo, 1989. Morgan Kaufmann Publishers Inc.

16. Балакирев В. С, Володин В. М., Цирлин А. М. Оптимальное управление процессами химической технологии (экстремальные задачи в АСУ). М.: Химия, 1978, 383 с.

17. Корн Г., Корн Т. Справочник по математике. Для научных работников и инженеров. М.: Наука, 1974, 832 с.

18. Poggio Т. and Girosi F. Networks for approximation and learning // Proceedings of the IEEE. V. 78, № 9, 1990. P. 1481-1497.

19. Park J. and Sandberg I. W. Universal approximation using radial-basis-functlon networks // Neural computation. 1991. V. 3, P. 274-257.