Авторы: Горобець О.В.
Источник: http://www.confcontact.com/2008dec/8_gorobets.htm
ЗАСТОСУВАННЯ СТАТИСТИЧНОГО МОДЕЛЮВАННЯ
ПРИ ПЕРСПЕКТИВНИХ РОЗРАХУНКАХ СКЛАДУ ТА РУХУ НАСЕЛЕННЯ
Прогнозування динаміки чисельності та структури населення, чисельності та склад сімей, режимів відтворення населення, різних демографічних процесів складає значну частину діяльності міжнародних, державних та неурядових організацій, закладів та наукових інститутів. Провідні демографи, економісти, статистики здійснили чимало глибоких та різноаспектних досліджень проблем моделювання відтворення населення. Процес моделювання зміни чисельності населення, використання математичних, демографічних, статистичних методів викладено у наукових і навчально-методичних працях вчених А.Я. Боярського, Г.С. Кільдишевої, С.С. Герасименка, Н.В. Ковтун, Г.І. Купалової, А.М. Єріної, І.К. Дрозда, Л.В. Черничука, В.Г. Швеця, П.Є. Шевчука.
Сучасний погляд на проблему демографічного прогнозування полягає у синтезі елементів моделювання та власне прогнозу. Ця методологія має назву потенційного аналізу, який синтезує два основних підходи: соціально-інтегративний та регіонально-типологічний.
В сучасній статистиці використовуються різні методи, які мають різну точність та беруть за основу різні моделі. Деякі з них дають характеристику зміни населення в цілому — це моделі, які засновані на використанні в прогнозуванні математичних функцій (лінійна, експотенційна, логістична). Зміни чисельності населення найчастіше не мають різких ривків та нагадують деякі математичні криві, тому виникає питання про згладжування фактичній динаміці населення за їх допомогою.
Метою дослідження є розкриття основ використання математичного моделювання при прогнозуванні чисельності населення.
Демографічні моделі призначені для характеристики стану населення, окремих елементів відтворення населення чи процесу відтворення в цілому. Термін «демографічні моделі» почав широко використовуватися в науковій літературі з початку 40-х років ХХ сторіччя.
Більшість демографічних моделей не можуть розкрити явище, що моделюється, з урахуванням багатьох чинників та складових. Використання демографічних моделей потребує абстрагування ряду характерних ознак, властивостей об’єкта моделювання, які чи є несуттєвими, чи вважаються несуттєвими, с точки зору задач, які вирішує моделювання. «Ще на початку 1990-х років, коли демографічні моделі демонстрували неістотні відхилення від фактичних даних, в демографічній літературі вказувалося на можливе настання непередбачуваних, кардинальних зрушень у відтворенні населення України внаслідок бурхливих соціальних, політичних, економічних та екологічних змін. Причиною цього є недетерміністичність соціальних і, зокрема, демографічних процесів. З одного боку, їх не можна виразити у вигляді певного закону, функції певного виду. Застосування кореляційно-регресійних моделей не гарантує, що встановлені статистичні закономірності будуть постійними чи змінюватимуться в майбутньому певним чином. З іншого боку, демографічний розвиток, як розвиток будь-якої системи, не є хаотичним, у ньому достатньо послідовності та порядку» [1; с. 41].
В сучасній статистиці демографічні моделі використовуються:
1) Для отримання кількісних характеристик демографічних процесів та явищ. Особливе значення ці моделі мають значення при визначенні узагальнюючих характеристик інтенсивності демографічних процесів (середня тривалість житті, нетто-коефіцієнт відтворення населення та ін.), які є ендогенними змінними відповідних демографічних моделей, що є основою демографічних таблиць;
2) Для вивчення закономірностей та чинників демографічних процесів при виявленні зв’язку між складовими моделей, як засіб кількісної оцінки виявлених зв’язків та залежностей, як засіб перевірки гіпотез. В демографічній статистиці метод моделювання – один з головних методів виявлення та аналізу причинно-наслідкових зв’язків та інших залежностей;
3) Для демографічного прогнозу, де використовуються при визначенні майбутніх тенденцій окремих демографічних процесів та їх кількісних характеристик на перспективу, також при перспективних розрахунків чисельності та складу конкретного населення;
4) Для поточних та ретроспективних демографічних розрахунків, коли відсутні показники статистики населення або вони не малодостовірні;
5) Для визначення характеру збору та обробки інформації про населення.
При сучасному моделюванні характерним є каузальний підхід до моделювання, тобто підхід, при якому на перший план виходить не зовнішня схожість, а вивчення внутрішньої сутності об’єкту моделювання. У той же час широко розповсюджені спроби розкрити закономірності демографічних процесів тільки кількісно у тих випадках, коли аналіз їх змісту проводити не можливо при сучасному рівні демографічної науки.
Демографічна модель виникає як абстрактна математична модель, що може бути віднесена до кожного з населення, відповідно до визначених обмежень. Методи,що використовуються дозволяють відрізняти прогнозування населення:
1) За типом математичних функцій, що використовуються;
2) За демографічними моделями відтворення населення;
3) За статистичними характеристиками динаміки;
4) За переходом віку.
Можливо сумісне використання різних методів та прийомів прогнозування з метою перевірки правильності їх вибору та проведення нових прогнозних зіставлень, що базуються на різних моделях.
Американський астроном Г. Притчетті в 1892 р. з метою прогнозу чисельності населення США використав параболу третього порядку. Дані, які були вирівняні за цією кривою за 1790 – 1880 рр., майже за кожний рік співпадали з фактичними. Показники прогнозу за параболою третього порядку на 1880 р. мали невелике (55 тис.) неспівпадіння з фактичними. Вважаючи, що зростання населення США буде йти тим же чином, вчений розрахував чисельність на 1000 років вперед. Однак, в подальшому різниця між розрахунковою та фактичною численністю збільшувалася. З’ясувалось, що параболу, за якою можливо описати зростання населення в минулому, не можливо використати для прогнозу. В основу математичної моделі вікового складу населення може бути покладено марківський процес із дискретним або безперервним часом і кінцевою кількістю станів процесу.
Розповсюдження для характеристики минулого та майбутнього розвитку населення має показова або експотенційна крива, яка бере до уваги не тільки час прогнозного періоду, але й основний показник розвитку населення – коефіцієнт його природного приросту.
Якщо коефіцієнт природного приросту прийняти, як незмінний за деякий період часу, то виходячи з експонтенційного закону росту населення, є можливість визначити його зміну:
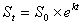(1)
де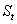 
– чисельність населення через t років;
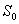– вихідна чисельність населення;
– основа натуральних логарифмів;
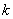– коефіцієнт природного приросту в долях одиниці [3; с. 493].
За наведеною формулою є можливість розрахувати чисельність населення через t років, якщо є показники за момент 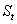та коефіцієнт природного приросту 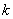. Однак за цією моделлю не можливо получити дані про вікову структуру населення, рівні народжуваності чи смертності, не має також можливості встановити пропорції між цими показниками.
Використавши екпоненційний закон, легко також встановити період часу, за який чисельність населення досягне встановленої величини. Для цього за формулою екпоненційного закону знаходять величину t, перед чим догу рифмують ліву та праву частини рівняння [5; с. 51]:
(2)
Оскільки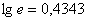 
, тому знаменник дробі буде складати 
. Замість 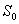можливо підставити будь-яку чисельність населення та визначити період t, через який базова чисельність 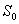при постійному 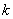досягне величини 
.
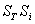Визначимо, коли чисельність Автономній республіці Крим буде становити 1500 тис. чол. при збереженні загального приросту за такими даними: чисельність на 1 січня 2008 року становила 1971,7 тис. чол. та середній коефіцієнт приросту (К) за 1998-2007 рік становить -6,2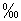
: 
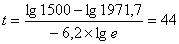(роки), тобто цей показник буде досягнуто в 2052 року.
Для розрахунку загальної чисельності через декілька років можливо використати наступну формулу [6; с. 89]:
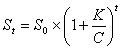(3)
де С – величина бази розрахунку (100 чи 1000).
За даними розрахунку на 1 січня 2018 року чисельність Автономній республіці Крим буде становити 1855 тис. чол. при збереженні загального приросту, тобто очікується зниження на 116,7 тис. осіб. Зниження чисельності можливо також підтвердити при дослідженні часткових та інтегральних індексів людського розвитку регіонів України. За даними Інституту демографії та соціальних досліджень НАНУ індекс демографічного розвитку Криму за період з 2000 – 2005 рр. зменшився на 0,054, а рейтинг АР Крим в цілому по Україні впав з 24 до 13 [2; с. 317].
Недоліком цього методу можливо вважати те, що коефіцієнт природного приросту вважається постійним в продовж багатьох років. Це припущення відрізняється від дійсності: у 2002 році він становив по Криму - 6,7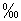, у 2004 р. - 6,1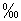, у 2006 році - 5,3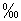, у 2007 році - 6,7.
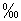Логістична функція дає характеристику такому зростанню, який спочатку має бистріший темп, продовжується до певного моменту, а потім стає більш повільним та в кінці досягає нуля [5; с. 54]:
(4)
де 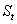– чисельність населення в момент t;
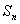– чисельність населення в момент максимального росту;
t – час;
, 
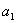– параметри функції.
Початківцем прогнозування чисельності населення за логістичною кривою став бельгійський вчений ХІХ ст. Р.Ф. Ферхюст. Подальший розвиток цей метод получив в працях американських вчених початку ХХ ст. Р. Пірля та Л. Ріда. У відповідності до теорії Пірля – Ріда в логістичній кривій є взаємозв’язок між темпами росту населення та його абсолютною чисельністю. Оскільки територія держави постійна, ця залежність переходить в залежність між темпами росту населення та його щільністю. Спочатку вона швидко зростає, потім, зустрівши подальший опір середи, зменшується, доходячи до нуля. Коли біолог Р. Пірль та математик Л. Рід придали логістичній кривій біологічне обґрунтування, вони використовували її за для вирівнювання емпірічних даних про чисельність населення. Для населення США та Швеції вирівнювання показало порівняно невеликі розходження між емпірічними та вирівняними даними, що дозволило проводити прогнозування за логістичною кривою.
Поєднання таблиць смертності та таблиць народжуваності дозволяє створити дискретну модель відтворення населення. Його система співвідношень між змінними показниками співпадає з розрахунками, які використовуються при розрахунках майбутньої чисельності населення за методом пересування за віком. З метою проведення аналізу більш частіше користуються математичною моделлю, що є аналогом цієї моделі, під назвою «інтегральне рівняння відтворення населення». Ці моделі застосовуються при дослідженні впливу народжуваності та смертності на структуру населення та їх зумисного впливу на темпи росту населення. Важливим елементом цього аналізу є модель сталого населення.
В останні роки зростає увага до використання методів і практичного використання імовірнісного прогнозування. Імовірнісний підхід при обчисленні перспективної чисельності населення за статево - віковими групами, як і більшість детерміністичних методів демографічного прогнозування, використовує когортно – компонентний метод та пересування вікових груп. Показники по окремих компонентах природного та механічного руху на перспективу отримуються за допомогою залучення різних методів: експертної думки, аргументованого підходу, методу динамічних рядів, аналізу похибок історичних прогнозів, умовного імовірнісного прогнозування.
Неточності, які мали місце в демографічних прогнозах минулого, пов’язані з такими помилками: недостовірність вихідної інформації та неадекватність сформульованих припущень про перспективу змін демографічних процесів. Тому найвірнішим критерієм точності прогнозів населення є збіг прогнозних і фактичних даних. Але таке порівняння можливо або після закінчення терміну прогнозу, або при ретроспективному прогнозуванні. При зіставленні прогнозних і фактичних даних можна використовувати абсолютну і відносну різниці розбіжностей, які називають абсолютною і відносною помилками прогнозу. При зіставленні різних методів прогнозування використовують середню квадратичну помилку прогнозу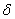 
, що обчислюється за формулою [5; с. 55]:
(5)
де 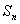– прогнозована чисельність;
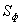– фактична чисельність;
п – число величин, що зіставляються.
Менша величина середньої квадратичної помилки свідчить про успішніший прогноз.
Дослідник питань економічного прогнозування американський вчений Г. Тейл запропонував вважати мірою помилки прогнозу коефіцієнт відповідності, в чисельнику якого береться середня квадратична помилка, а в знаменнику - середня квадратична з фактичних даних. Коефіцієнт невідповідності розраховується по формулі [5; с. 55]:
(6)
При V=0 має місце випадок повного збігу прогнозних і фактичних даних, V< 1 свідчить про незмінність приростів динаміки, V>1 означає, що прогноз дає гірші результати, ніж припущення про незмінність даного явища.
В деяких випадках надійність прогнозу визначається за допомогою показника вірогідності його реалізації, який пов'язаний з побудовою довірчих інтервалів прогнозу. Довірчий інтервал визначається виходячи з величини середньої квадратичної помилки фактичних даних від розрахункових і вірогідності можливої розбіжності. При вірогідності 0,997 величина довірчого інтервалу встановлюється в розмірі ±3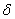, при вірогідності 0,954 вона рівна ±2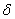, при вірогідності 0,683 ±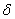. Отже, чим вища надійність прогнозу, тим нижча його точність, і навпаки.
Таким чином були розглянуті методи статистичного моделювання чисельності населення, визначені недоліки цих методів та можливості їх застосування в сучасній демографічній статистиці.
В якості подальшого напряму дослідження необхідно дослідити принципи використання прогнозів за демографічними моделями та за статистичними характеристиками динаміки.
Список використаної літератури
1. Комплексний демографічний прогноз України на період до 2050 р. (колектив авторів)/ за ред. чл.-кор. НАНУ, д.е.н., проф. Е.М. Лібанової. — К.: Український центр соціальних реформ, 2006.— 138 с. — ISBN 966-8998-22-7.
2. Людський розвиток регіонів України: аналіз та прогноз (колективна монографія) / за ред. чл.-кор. НАНУ, д.е.н., проф. Е.М. Лібанової. — К.: Ін-т демографії та соціальних досліджень НАН України, 2007.— 328 с. — ISBN 978-966-02-4481-8.
3. Медков В.М. Демография: Учебник. 2-е изд. — М.: ИНФРА-М, 2008. — 683 с.— (Высшее образование). — ISBN 978-5-16-002084-6.
4. Статинформация: Демографическая информация. Річна статистична інформація. — Режим доступу:http://sf.ukrstat.gov.ua/ukgdem.htm
5. Статистика населения с основами демографии: [Учеб. для вузов по спец. "Статистика" / Г. С. Кильдишев, Л. Л. Козлова, С. П. Ананьева и др.]. — М. : Финансы и статистика, 1990. — 310,[2] с. : ил.; 22 см. — Авт. указаны на обороте тит. л.. — Библиогр.: с. 309 (33 назв.). — ISBN 5-279-00305-0.
6. Тихомиров Н.П. Демография. Методы анализа и прогнозирования: Ученик для вузов / Н.П. Тихомиров. — М.: Экзамен, 2005. – 256 с. (Серия «Учебник Плехановской академии»). — ISBN 5-472-01119-1.
