Методические указания к расчетной работе «Моделирование оптического канала» по курсу «Оптико-электронные приборы и системы» (для студентов специальности 7.090902 «Научные, аналитические и экологические приборы и системы») / Хламов М.Г. – Донецк: ДонНТУ, 2004. – 33 с
1.1. Математическое моделирование оптического канала и сигналов
1.1.1. Спектр поглощения. При прохождении потока излучения через газообразные среды в различных областях спектра излучения имеют место изменения величины потока излучения обусловленные поглощением излучения различными компонентами газообразной среды.
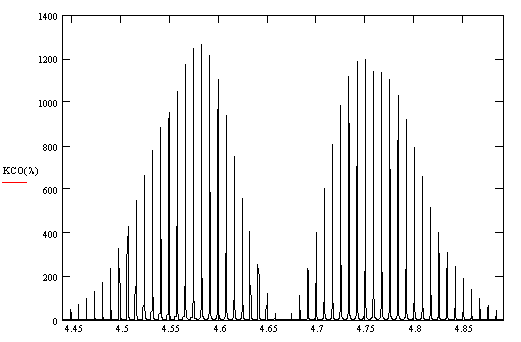
С колебательным и вращательным движениями молекул газа связана форма электромагнитного поля молекулы, зависящая одновременно от степени симметрии молекул газа и ее молекулярной массы. При этом молекулы могут быть строго симметричными и неполно симметричными различной степени симметрии. Полно симметричные молекулы имеют единственную полосу поглощения. Неполно симметричные молекулы, в зависимости от степени симметрии, имеют несколько полос поглощения. С ростом степени не симметрии число полос поглощения возрастает. С ростом молекулярной массы длина волны центра полос поглощения возрастает. Поглощение носит квантовый характер и связано с распределением энергии электронов, вращательного и колебательного движений по энергетическим уровням. Поглощение кванта энергии переводит молекулу в возбужденное состояние, в котором она находится tв » 10-6 с. Из возбужденного состояния молекулы возвращаются в исходное, при этом спонтанно излучается квант энергии. Каждая полоса поглощения может содержать две или три ветви образующих колебательно – вращательную полосу спектра. Полоса поглощения спектра носит линейчатый характер, показанный на рис. 3. Расчеты поглощенной энергии, дающие удовлетворительные результаты, выполняются при высоком разрешении по длине волны (на каждую линию спектра должно приходиться не менее 10 … 12 опорных точек расчета), что повышает степень их трудоемкости, но остаются единственно возможным методом для почти монохроматических источников излучения, которыми, например, являются полупроводниковые лазеры. При одинаковой точности расчетов для источников излучения с шириной спектра соизмеримой с шириной полосы поглощения более экономичными являются методы, основанные на учете интегрального коэффициента поглощения. Интегральный коэффициент поглощения ИК-излучения получается путем осреднения линейчатого спектра поглощения за интервал Dl*. Длина интервала осреднения Dl* выбирается не менее расстояния между линиями в спектре поглощения. В расчетной работе интервал осреднения принят равным расстоянию между линиями в спектре поглощения. Это ведет к уменьшению объема вычислений в 10 … 12 раз.

Рисунок 3 - Пример спектра поглощения трехатомного газа (молекулы
линейного типа)
1.1.2Модель оптического канала. На первой стадии математического моделирования, оптический канал (ОК) определим как слой тестируемого вещества, через который проходит, испытывая поглощение, поток излучения. По мере учета влияния различных факторов, определение канала будет уточнятся.
Модель ОК должна представлять собой зависимость концентрации ингредиента от параметров выходного сигнала канала и эта зависимость устанавливается на основании следующего.
Изменение однородного и монохромного потока излучения, проходящего через вещество описывается законом Ламберта - Бугера:
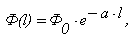 (1)
(1)
где Ф0 - поток излучения на границе тестируемого вещества;
a - показатель поглощения;
l - длина пути (трассы) излучения в тестируемом веществе.
Оптическая плотность вещества устанавливается законом Беера в виде:
D = a×l = k С×l , (2)
где С - концентрация активной компоненты вещества, поглощающего излучение;
k - удельный показатель поглощения.
Оптическая плотность вещества зависит от внешних условий: температуры и давления. Эти факторы в метеорологии [6], учитываются в виде эквивалентной длины трассы:
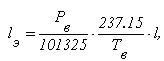 (3)
(3)
где давление Рв измеряется в [ Па ], а температура Tв - [ 0 К ]. В ИК-спектрометрии влияние давления и температуры учитывается более сложным образом: от давления сильно зависит полуширина спектральной линии поглощения и в меньшей от изменения температуры, огибающая спектра полосы тоже прямо пропорциональна изменению давления и обратно пропорциональна квадратному корню изменения температуры.
Положим, на входе ОК действует излучение с равномерным спектром, как показано на рис. 4. На волне l0 согласно закону Ламберта - Бугера между поглощенным, входным и выходным потоками ОК устанавливается связь:

Или, что тоже самое:
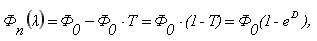 (4)
(4)
где Т – коэффициент пропускания оптического канала.
Приведенное соотношение иллюстрирует рис.5.

Для окрестности lп0 т.е. l0 ± Dl/2 процесс поглощения частотно зависим и определяется функцией интегрального коэффициента поглощения . Эта зависимость учитывается следующим образом:
 (6)
(6)
D(l,С) = Kинт(l)×lб×С/100; (7)
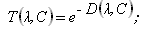 (8)
(8)
Коэффициент передачи оптического канала определяется как:
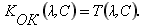 (9)
(9)
Пример АЧХ ОК приведен на рис.6.
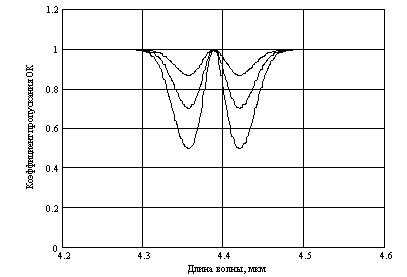
Рисунок 6 – Пример АЧХ оптического канала
Чувствительность измерителя определяется длиной трассы измерительного канала. Эту длину рекомендуется устанавливать соотношением:
 (10)
(10)
Полученное выражение используется для построения амплитудно-частотной характеристики ОК , включаемой в отчет по расчетной работе. Пример расчета спектральной характеристики оптического канала KОК(l, С) приведен в приложении Б.
Поток излучения, создаваемый электролюминесцентным источником и направляемый на облучение ОК , представляет собой входной сигнал ОК . Этот сигнал задан функцией sи(l)={ f3 , f4} , представляющий собой нормированную спектральную плотность потока излучения. Определим спектральную плотность потока входного сигнала оптического канала следующим образом:
SвхОК(l) = Su0 × su(l) (11)
Поток излучения, прошедший слой тестируемого вещества, образует выходной сигнал ОК . Этот сигнал содержит информацию о концентрации ингредиента в тестируемом веществе. Описывается он в следующем виде:
SвыхОК( l , C ) = SвхОК( l ) × KОК( l , C ). (12)
Обе функции представляются графически, причем график функции SвхОК(l) имеет вид SвыхОК( l , C=0) , а график функции SвыхОК( l , C ) для различных значений концентрации ингредиента приведен на рис.7.Полученные выражения спектральных плотностей потоков излучения используются для построения спектров входного и выходного сигналов ОК , включаемых в отчет по расчетной работе. Спектр выходного сигнала строится при максимальном значении концентрации ингредиента. Пример построения этих характеристик сигналов приведен в приложении Б.
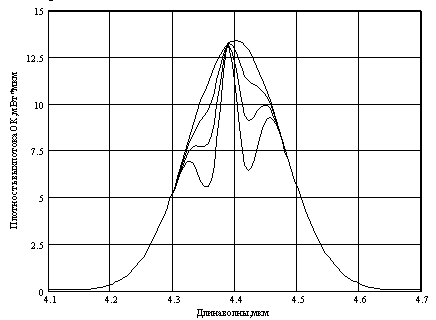
Рисунок 7 – Спектр выходного сигнала ОК при различных концентрациях ингредиента
Информация о концентрации ингредиента в выходном сигнале представлена в виде изменения формы спектра. Входной величиной всех фотоприемников является поток излучения, а не отдельные спектральные составляющие. Выходной сигнал фотоприемника пропорционален интегральной характеристике сигнала:
Uфп = Sинтс × ФвыхОК(С); (13)
 (14)
(14)

ФвыхОК(С)=C×W;
Рисунок 8 – Представление ОК звеном измерительной цепи
Результатом измерений должна быть концентрация, а не величина выходного потока. Для этого следует установить обратную зависимость:
С = W-1×ФвыхОК(С). (15)
Одной из задач расчетной работы является установление зависимости (15). При выполнении интегральных преобразований рекомендуется использование справочной литературы [7].Зависимость концентрации от потока излучения оказывается более наглядной и воспринимаемой, если она устанавливается не для потока излучения, а его относительного изменения:
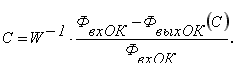 (16)
(16)
Зависимости (15) и (16) представляются в графической форме. Пример расчета и графического представления зависимостей приведен в приложении Б. Обратная функция W-1 представляет собой решение уравнения (16) относительно С. В (16) выходной поток оптического канала входит в виде интегрального соотношения (14) со сложной зависимостью от длины волны. Это значительно осложняет поиск решения в аналитическом виде, но за это решение может быть принято табличное представление зависимости, где аргумент и функцию легко поменять местами.