Бреслер ПИ Оптические абсорбционные газоанализаторы и их применение

Бреслер Павел Ильич

Оптические абсорбционные газоанализаторы и их применение. – Л.: Энергия. Ленингр. отд-ние, 1980. – 164 с.

1-3. Избирательное поглощение лучистой энергии в газах

Исследования поглощения газами ЛЭ очень важны для разных отраслей физики и техники, в частности: атмосферной физики, теории строения атомов и молекул, прикладной, в том числе бездисперсионной, спектроскопии. Первый закон поглощения был сформулирован Бугером более двухсот лет тому назад. Закон Бугера устанавливает прямую пропорциональность между интенсивностью падающего потока ЛЭ и количеством энергии dI×dn поглощаемой бесконечно тонким слоем du вещества в спектральном интервале dn:

dI×dn = K×I×du×dn, (1-1)

где K—коэффициент поглощения.

Экспериментальная проверка закона Бугера была произведена С. И. Вавиловым в 1919г. Он установил, что закон Бугера соблюдается в очень широком диапазоне интенсивности потока ЛЭ, (10^–18 – 10¹) Вт/см². Отклонения от него наблюдаются лишь в случаях, когда длительность возбужденного состояния молекул поглощающего вещества очень велика.

Второй закон поглощения — закон Ламберта — является интегральной формой закона Бугера для изотропной среды:

Idn = I₀×e^–K^×udn, (1-2)

где I₀—интенсивность параллельного потока ЛЭ в спектральном интервале dn, падающего на слой вещества толщиной u; I—интенсивность потока, прошедшего слой u.

Согласно третьему закону поглощения, называемому законом Беера, коэффициент поглощения для смеси J поглощающих веществ:

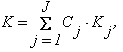(1-3)

где К,— коэффициент поглощения j-го- компонента;

С,— концентрация j-го компонента в смеси.

Многочисленные эксперименты целого ряда исследователей показали, что поглощение ЛЭ в реальных средах, в том числе и в газах, почти никогда не подчиняется законам Ламберта и Беера. Было установлено, что отклонения от этих законов бывают кажущимися и истинными. Кажущиеся отклонения обусловлены немонохроматичностью используемых потоков ЛЭ и зависимостью коэффициента поглощения от частоты (длины волны) света, а истинные отклонения—взаимодействием молекул поглощающей среды, например ассоциацией молекул поглощающего газа (например, HF) при увеличении его парциального давления.

В приборах бездисперсионной спектроскопии обычно имеют дело с немонохроматическими потоками ЛЭ. Поэтому следует в первую очередь рассмотреть влияние этого обстоятельства на вид зависимости поглощаемой газом энергии от параметров поглощающего вещества.

Поток ЛЭ, поглощенный в слое газа с эквивалентной толщиной u (т. е. с толщиной 100%-го газа, давление которого приведено к нормальному атмосферному Рн):

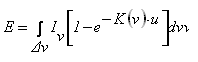(1-4)

Интегрирование этого выражения возможно при известных I_n и K(n). Если I_n = const и K(n) = const в интервале частот Dn, то очевидно, что закон Ламберта будет выполняться. Задача интегрирования выражения (1-4) в ИК-области спектра рассматривалась во многих работах, в частности в работах У. Эльзассера. Основные трудности возникают при этом из-за сложного вида функции K(n). Как известно, для ИК-области характерны так называемые колебательно-вращательные полосы поглощения, представляющие собой последовательности линий поглощения, контур каждой из которых определяется межмолекулярными соударениями и описывается выражением:

(1-5)

где 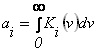—интегральная интенсивность i-й линии; d_i — полуширина линии;' n_0i — центр линии.

Коэффициент поглощения K(n) полосы выражается суммой коэффициентов поглощения отдельных линий:

(1-6)

Для вычисления ряда (1-6) вводились различные допущения о характере изменения a_i„ d_i и n_0i в пределах колебательно-вращательной полосы. У. Эльзассер рассматривал полосу поглощения как бесконечную последовательность одинаковых по интенсивности (a_i = const) и полуширине (d_i = d) равноотстоящих линий.

Автор рассмотрел [2] модель полосы поглощения, в которой равноотстоящие линии равной полуширины d имеют распределение интенсивности в каждой из двух ветвей полосы, соответствующее распределению молекул по вращательным уровням энергии. На рис. 2-7 приведены графики функции K(n), вычисленные для полосы 2350 см^-1 (4,26 мкм) СО₂ для трех значений d с использованием принятой модели полосы. Исследуя указанную модель полосы, можно показать, что интегральное поглощение ИК-излучения в полосах целого ряда классов молекул при толщинах слоев газа, соответствующих применяемым в ОПАГ, определяется «законом квадратного корня»:

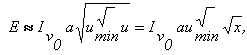(1-7)

(1-8, 1-9)

а при , т.е. при x < 1 — законом поглощения, близким к линейному:

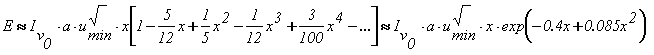
где a – интегральная интенсивность полосы поглощения; I_n0 интенсивность падающего на слой газа излучения в центре полосы n₀, принимаемая постоянной в пределах полосы; В—вращательная постоянная молекулы; m = =Bhc/(kT), причем k—постоянная Планка, с—скорость света в вакууме, k—постоянная Больцмана, Т— абсолютная температура газа; р—коэффициент, равный 1 для двухатомных молекул, линейных несимметричных молекул и сферических волчков и равный 2 для линейных симметричных молекул типа CO₂; d = 2Br — расстояние между центрами двух соседних вращательных линий, принятое одинаковым в пределах всей полосы; R₁ – коэффициент, равный 18 для сферических волчков, и 16,8—для остальных указанных выше классов молекул; R₂—коэффициент, соответственно равный 1,52 и 1,46.

Вверх