Цуканов А. В., доц. Дегтяренко И. В. Обоснование применения wavelet декомпозиции сигналов для борьбы с джиттером в телекоммуникационных системах

ОБОСНОВАНИЕ ПРИМЕНЕНИЯ WAVELET ДЕКОМПОЗИЦИИ СИГНАЛОВ ДЛЯ БОРЬБЫ C ДЖИТТЕРОМ

В ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМАХ

Цуканов А. В., доц. Дегтяренко И. В.

Источник: Компьютерный мониторинг и информационные технологии – 2009/ Материалы четвёртой научно-технической конференции студентов, асперантов и молодых учёных. – Донецк, ДонНТУ – 2009, с.130-131

Одной из главных тенденций современных телекоммуникационных систем является их цифровизация. В любой цифровой системе важным параметром является период дискретизации. И от того, насколько точно он выдерживается во многом зависит качество работы системы. Нежелательные фазовые и/или частотные случайные отклонения периода дискретности передаваемого сигнала называется джиттером. Он может возникать вследствие нестабильности задающего генератора, изменений параметров линии передачи во времени и различной скорости распространения частотных составляющих одного и того же сигнала [1]. Джиттер является одной из основных проблем при проектировании устройств цифровой электроники, в частности, цифровых интерфейсов. Недостаточно аккуратный расчет джиттера может привести к его накоплению при прохождении цифрового сигнала по тракту и, в конечном счёте, к неработоспособности устройства.

В области телекоммуникаций с джиттером и его последствиями борются с помощью буферной памяти, устройств ФАПЧ, применением специальных линейных кодов, созданием выделенных сетей тактовой синхронизации. В основном данные решения предполагают аппаратную реализацию. Однако в некоторых случаях имеет место постобработка и восстановление сигналов программными средствами. Данная работа посвящена развитию средств минимизации джиттера возникшего на этапе дискретизации сигнала. По сути, задача удаления джиттера сводится к восстановлению характеристик стохастически дискретизированных сигналов.

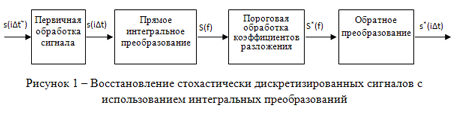
Одним из новых, мало исследованных на сегодняшний день подходов к восстановлению стохастически дискретизированых сигналов является метод, в котором используются интегральные преобразования [2]. Концепция данного метода может быть представлена в виде схемы (см. рис. 1).

В соответствии с предложенной структурой на первом этапе производиться преобразование неравномерно дискретизированного сигнала s(iΔt^~) к сигналу с постоянным шагом дискретизации s(iΔt). Далее производится прямое интегральное преобразование, переводящее сигнал из временного представления в частотное. Алисные компоненты при стохастической дискретизации имеют широкополосный шумоподобный спектр [3], и соответственно могут быть минимизированы путем пороговой обработки коэффициентов разложения S(f). После этого производится обратное преобразование, т.е. генерируется сигнал s^*(iΔt) имеющий постоянный шаг дискретизации с уменьшенными уровнями алиасных компонент. В качестве интегрального преобразования в данной структуре могут быть использованы дискретное преобразование Фурье (DFT) или его разновидности дискретное косинусное преобразование (DCT) и дискретное синусное преобразование (DST) [2].

Но эта структура не является универсальной, из-за того, что может использоваться только для восстановления стационарных сигналов имеющих линейчатый спектр, т.к. преобразование Фурье производит усреднение характеристик сигнала на всем участке обрабатываемого сигнала, вследствие чего, теряются его локальные особенности.

Избежать этой проблемы можно с помощью использования в качестве интегрального преобразования вейвлет декомпозицию сигналов, которая не обладает указанными выше недостатками [4]. Это разложение имеет вид

, (1)

где ψ(t) – материнская функция (материнський вейвлет);

а – коэффициент, задающий масштаб вейвлета (обретен частоте);

b - коэффициент, задающий положение вейвлета (пропорционален времени).

На практике чаще используется дискретное вейвлет преобразование сигналов, т.к. его можно реализовать с помощью набора НЧ и ВЧ фильтров. Эти фильтры связаны между собой и называются квадратурными зеркальными фильтрами. В результате прохода через ВЧ-фильтр получаются детализирующие коэффициенты разложения, а в результате НЧ фильтрации - коэффициенты аппроксимации.

Достоинствами этого способа декомпозиции сигналов является то, что учитываются все локальные особенности сигналов, в которых и заключена передаваемая информация. Кроме того, данное разложение просто в реализации и не вносит дополнительной избыточности в исходные данные. Обратное преобразование также реализуется с использованием фильтров.

Таким образом, в данной работе предложен новый способ борьбы с джиттером, возникшим на этапе дискретизации сигналов. Данный способ основан на использовании пороговой обработки вейвлет разложения сигнала. Он может также быть использован для восстановления потерянных отсчетов цифрового сигнала. Использование данного способа в телекоммуникационных системах позволит повысить достоверность передачи информации.

Литература

1. Джулиан Данн. Джиттер. Теория. Audio Precision. http://www.ixbt.com/proaudio/jitter-theory-part3.shtml

2. Дегтяренко И.В._, Афанасьев Д.Н. Алгоритм восстановления стохастически дискретизированых сигналов, Наукові праці ДонНТУ. Серія «Обчислювальна техніка та автоматизація. Випуск 15.- Донецьк: ДонНТУ, 2008- с.36-41.

3. Bilinskis I. Digital alias-free signal processing. – Willie, 2007. – 430 p..

4. Дьяконов В.П. Вейвлеты. От теории к практике. – М.: СОЛОН-Р, - 2002. – 448 с.

<<назад