Параметрическое моделирование дискретных стохастических процессов по известным входным и выходным сигналам
Анохин В. В.
Источник: soft.mail.ru/journal/pdfversions/378_anokhin.pdf
В настоящей работе кратко рассмотрены теоретические основы для решения обратной задачи применительно к процессам построения дискретных моделей по наблюдаемым (измеряемым) сигналам. Решение обратной задачи включает формирование или выбор: структуры модели изучаемого процесса; критерия качества идентификации; алгоритмов идентификации; критерия и методов верификации (подтверждения) модели. В статье рассмотрены вопросы параметрического моделирования стохастических процессов и приведены описания модельных структур на основе конечной совокупности настраиваемых параметров.
Задача
Параметрическое моделирование стохастических процессов. Описание модельных
структур процессов на основе конечной совокупности настраиваемых параметров.
Математические описания имитационных и прогнозирующих моделей процессов.
Программные средства
MATLAB, Simulink, Signal Processing Toolbox, Signal Processing Blockset.
Результаты
Изложены основы параметрического моделирования процессов и систем. Приведены
примеры и тексты программ для прогнозирования процессов. Представлены
математические описания имитационных и прогнозирующих моделей процессов.
Выбирая полный диапазон от 1 до N + p, получаем взвешенный случай, т. к. он включает пред- и постоконное взвешивание данных (отсутствующие данные приравниваются к нулю). Выбирая диапазон суммирования от 1 до N, получаемпредвзвешенный случай, поскольку данные, предшествующие y(1), полагаются равными нулю. Если взять диапазон суммирования от p+1 до N, имеем невзвешенный случай, поскольку используются только имеющиеся отсчеты данных. Взвешенный случай получил название автокорреляционного метода линейного предсказания, невзвешенный — ковариационного метода линейного предсказания.
Программная реализация Signal Processing
Toolbox имеет несколько функций для параметрического моделирования
авторегрессонных процессов, среди которых выделимследующие:
lpc.m — метод линейного предсказания;
aryule — м етодЮло-Уокера;
arburg — м етод Берга;
arcov — ковариационный метод;
armcov — модифицированный ковариационный метод.

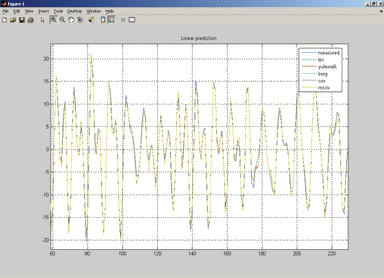
Рис. 1. Одношаговое прогнозирование процесса: результат работы программы ex1_parmod.m (показан фрагмент наблюдаемого процесса и его прогнозируемые значения).
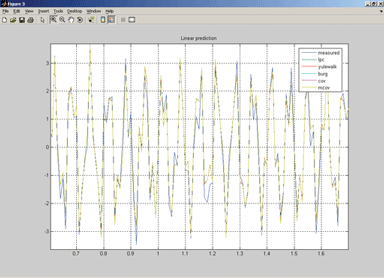
Рис. 2. Одношаговое прогнозирование процесса: результат работы программы mypred.m (показан фрагмент наблюдаемого процесса и его прогнозируемые значения).
Синтаксис вызова всех этих функций
одинаков и в минимальном варианте таков:
a=func(y,p);
где a — искомые оценки ˆak, y — массив отсчетов данных, p — порядок. Перед темк
ак проиллюстрировать работу этих функций и использовать полученные результаты —
маленькая справка о встроенной функции filter. Функция filter вычисляет значения
выходного процесса y(n) в соответствии с уравнением(2). Синтаксис вызова
следующий:
y=filter(b,a,u);
где b — коэффициенты числителя, a — коэффициенты знаменателя передаточной
функции (1), u — входной сигнал; в (2) в качестве u используется e.
После этого шага мы полностью готовы к построению моделей процессов, их
прогнозированию и спектральному оцениванию.
В Приложении 1 приведен текст простой программы ex1_parmod, в которой сначала задаются параметры фильтра, формирующего наблюдаемый процесс y, и формируется исходный сигнал (строки 1–4). Строки с 5 по 10 — это непосредственное использование упомянутых функций параметрического оценивания по их «боевому» назначению, т. е. получению оценок AR-параметров. После получения оценок этих параметров вычисляется линейное предсказание (строки 11–15) и строятся графики наблюдаемого процесса и линейного предсказания (строки 16–18). Поскольку в прогнозирующих моделях AR-параметры используются в качестве MA-параметров, в строках 11–15 перед ними ставится знак минус (смена знака) и не используется первый параметр, равный единице, т. к. это весовой коэффициент, на который умножается текущий выходной отсчет, стоящий слева от знака равенства. На рис. 1 показан результат работы программы (фрагмент полного графического построения). Программа-близнец mypred (Приложение 2) выполняет те же действия за исключениемтого, что наблюдаемый процесс — это сумма двух синусоид с аддитивным шумом. На рис. 4 показан увеличенный фрагмент полученного результата. Задача, решаемая программой ex1_parmod, м ожет быть решена и средствами Simulink с использовани емблок ов из Signal Processing Blockset (Signal Processing Blockset и Signal Processing Blockset/Estimation/Linear Prediction). На рис. 3 показана модель Simulink ex1_arestimate с результатами работы.

Рис. 3. Оценивание параметров
стохастического процесса: результат работы модели
Simulink ex1_arestimate.
Приложение 1. Программа ex1_parmod.m
1 e=randn(512,1);
2 a = [1 -2.2137 2.9403 -2.1697 0.9606];
3 b=1;
4 y=filter(b,a,e);
5 [a_lpc,e_lpc]=lpc(y,4);
6 a_lpc=real(a_lpc);
7 [a_yul,e_yul] = aryule(y,4);
8 [a_burg,e_burg] = arburg(y,4);
9 [a_cov,e_cov] = arcov(y,4);
10 [a_mcov,e_mcov] = armcov(y,4);
11 y_lpc=filter(-[0 a_lpc(2:end)],1,y);
12 y_yul=filter(-[0 a_yul(2:end)],1,y);
13 y_burg=filter(-[0 a_burg(2:end)],1,y);
14 y_cov=filter(-[0 a_cov(2:end)],1,y);
15 y_mcov=filter(-[0 a_mcov(2:end) ],1,y);
16 plot([y y_lpc y_yul y_burg y_cov y_mcov]), grid on
17 title(’Linear prediction’)
18 legend(’measured’,’lpc’,’yulewalk’,’burg’,’cov’,’mcov’)
Приложение 2. Программа mypred.m
1 t=(0:0.01:5.11)’;
2 y=2.2*sin(2*pi*15*t)+1.3*sin(2*pi*39*t)
+normrnd(0,.2,length(t),1);
3 a_lpc=real(lpc(y,4))
4 [a_yul,e_yul] = aryule(y,4)
5 [a_burg,e_burg] = arburg(y,4)
6 [a_cov,e_cov] = arcov(y,4)
7 [a_mcov,e_mcov] = armcov(y,4)
8 y_lpc=filter(-[0 a_lpc(2:end)],1,y);
9 y_yul=filter(-[0 a_yul(2:end)],1,y);
10 y_burg=filter(-[0 a_burg(2:end)],1,y);
11 y_cov=filter(-[0 a_cov(2:end)],1,y);
12 y_mcov=filter(-[0 a_mcov(2:end)],1,y);
13 figure
14 plot(t,[y y_lpc y_burg y_cov y_mcov]),grid on
15 title(’Linear prediction’)
16 legend(’measured’,’lpc’,’yulewalk’,’burg’,’cov’,’mcov’)
Литература
Литература
1. Анохин В. В. Модели динамических систем: технологии
построения в MATLAB // Exponenta Pro. Математика в
приложениях.— 2003.— №4.— С. 54–59.
2. Марпл С. Л. Цифровой спектральный анализи его
приложения.— М.: Мир.— 1990.— 584 с.48 с.