АНАЛІТИЧНІ МОДЕЛІ ДЛЯ ДОСЛІДЖЕННЯ ДИНАМІЧНИХ ПРОЦЕСІВ В ТЕЛЕКОМУНІКАЦІЙНИХ МЕРЕЖАХ
Воропавева А.А., Бессараб В.И.,
Донецкий национальный технический университет
Источник:Збірник тез доповідей дванадцятої Всеукраїнської (сьомої Міжнародної) студентської наукової конференції з прикладної математики та шнформатики СНКПМІ 2009
Для розробки моделей динамічних процесів в телекомунікаційних мережах останнім часом широко застосовують апарат ідемпотентних алгебр, [2], зокрема Max-Plus алгебру. Загальний підхід до опису процесів в ТМ мережі полягає в наступному. Нехай мережа складається з n-вузлів у кожному з яких є одно канальний пристрій обробки заявок (пакетів) і буфер в якому може відбуватися очікування обробки в черзі. Топологія мережі задається орієнтованим ациклічним графом  , де
, де  множина вершин графа, які відповідають вузлам мережі,
множина вершин графа, які відповідають вузлам мережі,  - множина дуг графа, що характеризують маршрути передачі заявок по мережі.
- множина дуг графа, що характеризують маршрути передачі заявок по мережі.
В структурі мережі виділяють особливі вузли. Множини вузлів мережі для якої виконується умова, що  розглядаються як джерела нескінченного потоку заявок (пакетів), що надходять до мережі. Заявки, які покидають мережу після обслуговування в вузлах i, для яких
розглядаються як джерела нескінченного потоку заявок (пакетів), що надходять до мережі. Заявки, які покидають мережу після обслуговування в вузлах i, для яких  називають множиною вузлів-приймачів заявок.
називають множиною вузлів-приймачів заявок.
У початковий момент часу всі пристрої обробки заявок в мережі вільні, черга заявок в кожному вузлі-джерелі має нескінченну довжину, а черги всіх інших вузлів i містять по ri –заявок, які готові до обслуговування пристроями.
Для формалізації процесу вводяться наступні позначення змінних:
 – тривалість обслуговування k-ї заявки в i-му вузлі мережі;
– тривалість обслуговування k-ї заявки в i-му вузлі мережі;
 – момент часу завершення обслуговування k-ї заявки в i-му вузлі мережі;
– момент часу завершення обслуговування k-ї заявки в i-му вузлі мережі;
 - момент надходження k-ї заявки в чергу на обслуговування в i-му вузлі мережі.
- момент надходження k-ї заявки в чергу на обслуговування в i-му вузлі мережі.
Передбачається, що  – невід’ємні випадкові величини з математичним очікуванням
– невід’ємні випадкові величини з математичним очікуванням  для всіх i=1…n та k=1,2….
для всіх i=1…n та k=1,2….
Для визначеності задають додаткові початкові умови процесу:
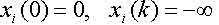 для k<0 та i=1,2…n;
для k<0 та i=1,2…n;
З урахуванням прийнятих позначень та припущень динаміка будь-якого вузла мережі описується в термінах Max-Plus алгебри [1] за допомогою рівняння:
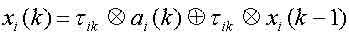 (1)
(1)
Для мережі з n вузлами, переходячи до керованої форми представлення рівняння (1) маємо два вектори:

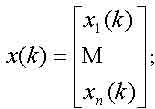
та діагональну матрицю обслуговування:

де  - загально прийняте позначення в Max-Plus алгебрі.
- загально прийняте позначення в Max-Plus алгебрі.
Тоді рівняння динаміки мережі з n вузлами у векторно-матричній формі матиме наступний вигляд:
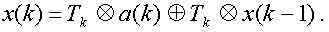 (2)
(2)
У випадку, коли черги вузлів не містять вимог, динаміка мережі може бути представлена за допомогою наступного рівняння:
 (3)
(3)
При моделюванні динаміки мережі з використанням рівняння (2) на процес обслуговування в вузлах завжди існують деякі обмеження, пов’язані з особливостями передачі інформаційних повідомлень, або специфікою протоколу, який використовується в мережі.
Як приклад застосування запропонованої методики, автором отримані характеристики середнього часу затримки для транспортних SDH-мереж, які використовуються для передачі голосового трафіку оператором мобільного зв’язку.
Литература
- Маслов В.П., Колокольцов В.Н. Идемпотентный анализ и его применение в оптимальном управлении. М.: Физматлит, 1994. 144 с.
- Min-plus and Max-plus System Theory Applied to Communication Networks. Jean-Yves Le Boudec, Patrick Thiran. LCA-ISC-I&C, EPFL, Lausanne, Switzerland. Volume 294/2004.
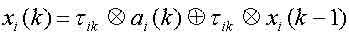 (1)
(1)  , де
, де  множина вершин графа, які відповідають вузлам мережі,
множина вершин графа, які відповідають вузлам мережі,  - множина дуг графа, що характеризують маршрути передачі заявок по мережі.
- множина дуг графа, що характеризують маршрути передачі заявок по мережі.  розглядаються як джерела нескінченного потоку заявок (пакетів), що надходять до мережі. Заявки, які покидають мережу після обслуговування в вузлах i, для яких
розглядаються як джерела нескінченного потоку заявок (пакетів), що надходять до мережі. Заявки, які покидають мережу після обслуговування в вузлах i, для яких  називають множиною вузлів-приймачів заявок.
називають множиною вузлів-приймачів заявок. – тривалість обслуговування k-ї заявки в i-му вузлі мережі;
– тривалість обслуговування k-ї заявки в i-му вузлі мережі; – момент часу завершення обслуговування k-ї заявки в i-му вузлі мережі;
– момент часу завершення обслуговування k-ї заявки в i-му вузлі мережі; - момент надходження k-ї заявки в чергу на обслуговування в i-му вузлі мережі.
- момент надходження k-ї заявки в чергу на обслуговування в i-му вузлі мережі. – невід’ємні випадкові величини з математичним очікуванням
– невід’ємні випадкові величини з математичним очікуванням  для всіх i=1…n та k=1,2….
для всіх i=1…n та k=1,2…. 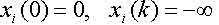 для k<0 та i=1,2…n;
для k<0 та i=1,2…n;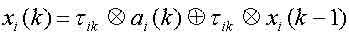 (1)
(1) 
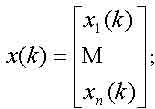

 - загально прийняте позначення в Max-Plus алгебрі.
- загально прийняте позначення в Max-Plus алгебрі.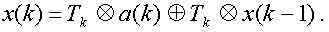 (2)
(2) (3)
(3)