10_____________________________Marcin Gajzler
is to show the possibilities of using fuzzy logic in the system assisting decision-making process in the contruction industry. The next phase consists of dividing the area of considered values. The typical way to do so is to evenly divide the area, which means to divide it into a specific number of fuzzy sets of identical width. Uneven area division of variable value is also possible. In this way membership functions in connection with original terms are created. Typical membership functions are triangle- or gauss-shaped.
The first thing to consider is the material type MT. The area was divided into three primary terms: A–spatula mortar, B–fine-grained mortar, C–coarse-grained mortar. Each of these terms corresponds to the value of the variable MT, which was defined in millimeters of aggregate grain thickness in the mortar.
0.0 0.2 0.4 [mm] MT
Fig. 1. Values of the variable MT
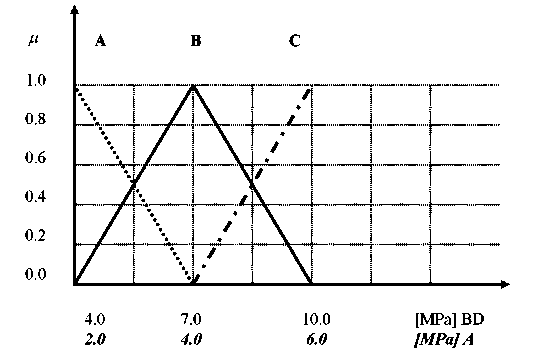
The next variable is the bending durability. Durability is a measurable value and it can be precisely defined. Still, also in this case the division of the value area had already been done, which served to separate 3 primary terms connected with the value of the variable BD: A–low durability, B–medium durability, C–high durability. The same was done as far as adhesion A is concerned. The only things changed were the ranges of the variable A, which was marked with a different font.