Известно [1, 2], что при изготовлении инструмента ори­ентация алмазных зерен, имеющих продолговатую форму (l/l>1,25), повышает его износостойкость и улучшает режущие свойства. Однако в настоящее время разработка технологии производства такого инструмента сдержива­ется отсутствием теории ориентации зерен.
    Форма удлиненных зерен наиболее точно аппроксимируется эллипсоидом. Ориентация может осуществляться в электрических, маг­нитных и электромагнитных полях.
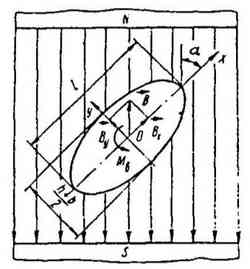
    Схема ориентации зерен в электромагнит­ном поле показана на рис. 1. На поверхность алмазов, предназначенных для ориентации, наносится покрытие, обладающее магнитными свойствами. Зерно, имеющее покрытие - объект с неоднородной внутренней массой. Ориентацию зерна обуславливают его масса, форма, соотношение линейных размеров, тол­щина и магнитные свойства покрытия, напря­женность поля.

    При ориентации алмазов магнитный момент М_м определяется произ­ведением векторов намагниченности и магнитной индукции , т. е. . Большую ось эллипсоида вращения примем равной длине l, а меньшую - полусумме ширины b и высоты h зерна, измеренного по двум проекциям (см. рис. 1). Величина магнитного момента в дан­ной системе координат,

где - угол между направлением линий ориентирующего поля и большей диагональю зерна (см. рис. 1).
    Для эллипсоида врашения компоненты вектора намагниченности связаны с компонентами вектора магнитного поля соотношением [3],

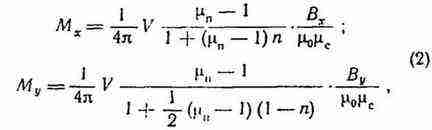
где V-объем покрытия алмаза; - магнитная проницаемость по­крытия и связки; - относительная магнитная постоянная; n=n_x - размагничивающий фактор, a n_y=( 1-n_x )/2.

где .

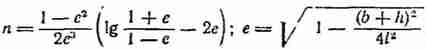    Объем покрытия , где lм, bм, hм - ли­нейные размеры металлизированного зерна. После соответствующих пре­образований (пренебрегая ввиду малости толщиной покрытия ) находим:

    Эффективность ориентации повышается в случае наложения коле­баний. При прохождении волны через абразивную массу удержание зерна окружающей его связкой резко ослабляется. В работе [4] пока­зано, что под действием колебаний происходит механическое разжи­жение сыпучей среды. Эффект разжижения почти мгновенно исчезает, если вибрации нет.
    Алмазы при разжижении насыпной массы свободно поворачивают­ся под действием электромагнитного поля в течение времени ( - период колебаний, - частота) на угол , где - угловая скорость вращения зерна. Вращательный момент, действую­щий на зерно,

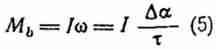
    Здесь I - момент инерции эллипсоида при вращении вокруг оси, перпендикулярной плоскости хоу (см. рис. 1): 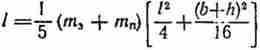где m_з и m_п - соответствгнно масса зерна и покрытия.
    Вращательный и магнитный моменты связаны соотношениями

    Приравнивая (5) и (6), находим или

где .
    Поворот множества зерен длинными осями в направлении магнитных линий поля - стохастический процесс, характеристики которого зависят от параметров вибрационного поля (частоты и амплитуды колебаний а). Для математического описания стохастического процесса введем функцию плотности вероятности f распределения углов , удовлетворяющую уравнению 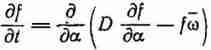, где средняя угловая скорость движения частицы , а коэффициент . При этом

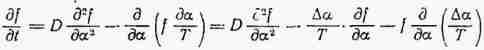
или, подставляя .

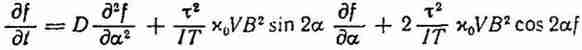
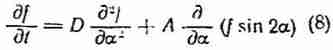
    Для установившегося процесса, т. е. при . Тогда

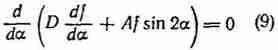
    Двукратное интегрирование уравнения (9) позволяет получить функ­цию плотности f_ст распределения углов ориентации в диапазоне в установившийся период

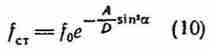
где f₀ - константа, определяемая из условия нормирования.
    Устойчивой ориентации в заданном направлении зерна достигают за некоторый промежуток времени, который назовем переходным пе­риодом и оценим его продолжительность. Чтобы определить время пе­рехода системы к установившемуся режиму, рассмотрим уравнение (8) для больших (но не бесконечных) моментов времени. В этом случае функцию плотности вероятности распределения углов можно представить в виде,

где - добавка, характеризующая отличие состояния системы в рассматриваемый момент от установившегося.
    Запишем 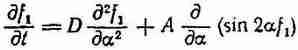или 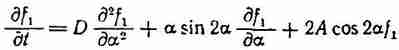    Решая последнее уравнение методом разделения переменных с заменой в виде , приходим к выражению:

    Левая часть данного равенства не зависит от , а правая - от t. Это может иметь место тогда, когда обе части уравнения [12] тожде­ственно равны некоторой постоянной величине, которую обозначим .     Решая первое из полученных дифференциальных уравнений , находим:

    Второе выражение представляет собой линейное дифференциальное уравнение с переменными коэффициентами, которое можно представить в нормальной форме путем замены переменных. Последующие преоб- разования приводят к уравнению Матье [5],

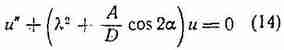
имеющему решение при определенных собственных значениях . Вви­ду симметричности функции плотности распределения углов оста­новимся па четном его решении. Для выражения (14) выбираем реше­ние, соответствующее і=1, т.е. так как нулевое собственное значение меньше нуля, а в пашем случае собственное значение >0). Последующие собственные значения можно не учитывать

    Время, за которое устанавливается режим, близкий к стационар­ному, получим из зависимости (13):

    Функция плотности вероятности распределения углов в пере­ходный период может быть получена нз выражения (11) с использова­нием зависимостей (10), (14) и (15).

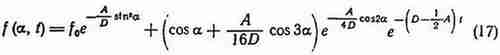
При выражение (17) преобразуется в (10).
    Причиной изменения ориентации алмазов при колебаниях смеси является неодинаковость момента количества движения, сообщаемого частицами связки, прилегающими к разным сторонам алмазного зерна. Так как удары каждой частицы связки при вибрации случайны, мож­но считать, что флуктуации скорости движения частиц , а флук­туации средней скорости группы из n частиц, прилегающих к половине поверхности алмазного зерна, , где n=(l/l₂)², l - длина ал­мазного зерна, l₂ - средний размер частицы связки. Отсюда можно оценить угол поворота алмазного зерна за период колебаний 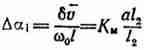( - коэффициент, учитывающий форму и массу зерен, силу их сцепления с частицами смеси).
    Взяв при расчете a = 2 мкм, l₂ = 10 мкм, l=200 мкм, К_м= 1, найдем, что рад. Значение , можно использовать для оценки порядка величины D. Если = 1 кГц, то .
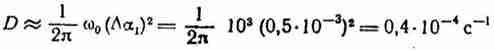    С помощью формулы (16) определим магнитную индукцию ориен­тирующего поля

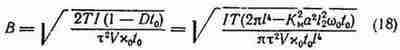
    Исходя из работы [4], можно считать, что = (0,05-0,2) Т. При­няв =0,1 Т, получим:

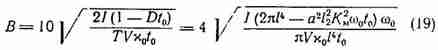
    После подстановки в (19) соответствующих величин находим

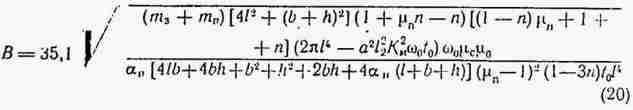
    Анализ данной зависимости показывает, что на магнитную индукцию ориентирующего поля влияют масса ( m_з ) и линейные размеры , толщина ( ), амплитудно-частотные характеристики накладываемых колебаний ( a, ) и их продолжительность ( t₀ ), характеристики связки ( l₂ , К_м ). При этом с увеличением массы зерна и частоты накладывае­мых колебаний необходимо повысить магнитную индукцию поля, а с увеличением толщины покрытия и продолжительности колебаний уменьшить.
    Для алмазных зерен продолговатой формы можно принять b=0,75l; h=0,63l [6]. Тогда после некоторых упрощений получим

    По формуле (21) вычислялось значение В, необходимое в случае изготовления кругов на связке M1 для ориентации алмазов АС4 и АС15, зерен кубонита КО с покрытием из никеля при 25-, 50- и 100%-ной степени металлизации (определяемой отношением ). Среднестатистическую массу зерна m_З измеряли во Всесоюзном науч­но-исследовательском институте метрологии. Применялся метод двой­ного взвешивания, что позволяло определять массу навески с точно­стью до 0,001 мг. Затем с помощью микроскопа МБС-2 подсчитывали число зерен в навеске и устанавливали среднестатистическую массу одного зерна (рис. 2).

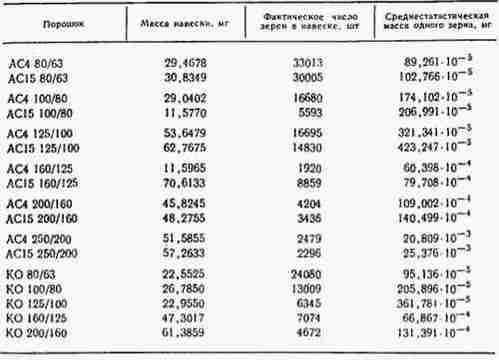
    В качестве примерарассчитаем В для ориентации алмазов АС15 125/100 с покрытием из никеля при 50%-ной степени металлизации. Используя данные рисунка 2 и работ [6, 7], примем l=184,3 мкм, b=138,9 мкм, h=111 мкм, =4 мкм, m_з=423,247*10^-5мг, m_п=0,5m_з, =100, t=20 с, =1000 Гц, =12,53*10^-7 Гн/м. Измерения показывают, что в зависимости от состава связки изменяется в широких пределах. Для связок, основой которых является медный, алюминиевый порошок или их смеси, данный показатель можно принять равный 1. Магнитная индукция вычисленная по формуле (21) для этих условий при трехкратном коэффициенте запаса, составит 0,06 Тл. Напряженность поля . Тогда для нашего примера Н=16143 А/м.
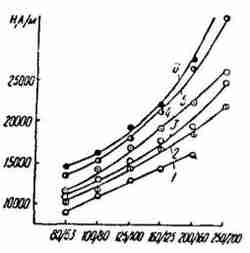
    Напряженность ориентирующего поля для алмазов и кубонита других зернистостей и марок приведена на рис. 3. Из него видно, что с увеличением зернистости ориентирующее поле должно иметь большую напряженность. Алмазы АС4 и АС15 одинаковой зернистости имеют несколько отличающуюся массу (см. рис. 2), а следовательно, и мас­су наносимого покрытия. Это приводит к тому, что для их ориентации нужна неодинаковая напряженность поля. Как показывают расчеты, расхождение в значениях напряженности не превышает 12%. Поэтому для практики, учитывая принятый коэффициент запаса, такое различие не существенно.

    С помощью описанной методики разработаны ряд способов ориен­тации зерен и соответствующая технологическая оснастка [8-10], а также технология изготовления шлифовальных кругов из зерен удли­ненной формы (l/b>2). В ее основу положена технология производ­ства, применяемая Полтавским заводом искусственных алмазов и ал­мазного инструмента. Круги для испытаний изготавливались на этом заводе и Воронежском заводе электровакуумных приборов. Микрошлиф поперечного сечения алмазоносного слоя такого круга показан на рис. 4
.     Полученный инструмент (по 10 кругов на каждой связке) испы­тывали в лаборатории технологии обработки специальных материалов Воронежского политехнического института. Использовались круги АЧК200х10хЗ на связках Ml, МП1 и Б156, которыми шлифовали образцы из твердого сплава ТТ10К8Б размером 20x20x7 мм, чугуна СЧ21-40 размером 130x50x50 мм, феррита 2000МТ1 и 1000НТ1 раз­мером 18x10x7 мм. Опыты осуществляли на станке мод. 3В642, до­полнительно оборудованном гидравлической продольной подачей. Ав­томатическое переключение продольной подачи проводилось вне зоны резания. В каждом опыте снимали по 500 г твердого сплава или фер­рита и 800-1000 г чугуна. При шлифовании чугуна и феррита техно­логической жидкостью служил 5%-ный водный раствор соответствен­но эмульсола ИСК-5у и ИХП-45Э; твердый сплав обрабатывали без охлаждения. Режимы шлифования: чугуна V_кр=33 м/с, S_пр=4 м/мин, t=0,015 мм/дв. ход; твердого сплава V_кр=28 м/с, S_пр=2 м/мин, t=0,04 мм/дв. ход;; ферритов V_кр=35 м/с, S_пр=1,5 м/мин, t=0,04 мм/дв. ход. Мощность шлифования измеряли ваттметром Н-348, шерохо­ватость поверхности - профилографом-профнлометром мод. 252. Рас­ход алмазов рассчитывали по методике, приведенной в работах [1, 11, 12], путем определения линейного износа круга. Во всех опытах заме­ры выполняли в восьми равномерно расположенных сечениях, причем в каждом нз них в пяти различных точках. Эксперименты повторяли от 5 до 16раз в зависимости отполя рассеивания результатов измерений в каждой точке. Число параллельных опытов выбирали так, чтобыпогрешность определения среднестатистического значения измеряемого параметра не превышала 3% при 95%-ной надежности.

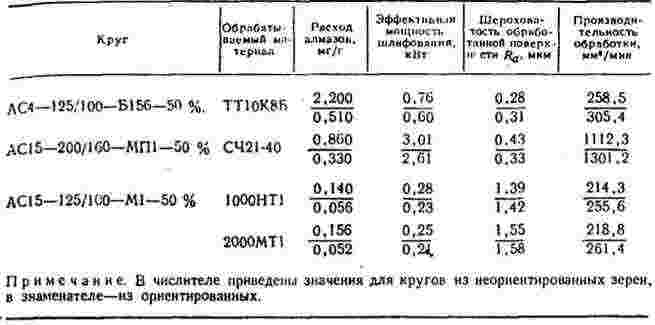
    Данные рис. 5 показывают, что износостойкость кругов с ориен­тированным расположением зерен значительно выше, чем обычных. Так, относительный расход алмазов при шлифовании кругами с ориен­тированными зернами твердого сплава в 4,3 раза меньше, чугуна - в 2,6, феррита в 2,5-3 раза. Одновременно со снижением расхода алмазов наблюдается некоторое увеличение производительности обра­ботки. Круги с ориентированными зернами характеризуются лучшей режущей способностью и правятся реже, чем обычные. При их исполь­зовании эффективная мощность шлифования снижается до 25%. Ше­роховатость поверхности при обработке кругами с ориентированными и неориентированными зернами примерно одинакова. Таким образом, экспериментальная проверка показала высокую эффективность кру­гов с ориентированными зернами. Описанная методика может служить основой для расчетов параметров ориентирующих полей, плотности распределения зерен и применяться при разработке технологии изго­товления кругов с управляемым внутренним строением.

    1. Зайцев А. Г. Влияние расположении алмазных зерен на процесс шлифования твердого сплава.- Вестн. машиностроения, 1977, № 8, С. 71-72.
    2. Зайцев А. Г. Влияние ориентированного расположения алмазных зерен на процесс шлифования.- В кн.: VI междунар. конф. «Intergrind-79» : Сб. материалов. Будапешт, 1979, т. 2, С. 737-742.
    3. Ландау Л. Д., Лифшиц Е. М. Электродинамика сплошных сред. - М.: Физматгиз, 1959. - С. 532.
    4. Блехман И. И., Джанелидзе Г. Ю. Вибрационное перемещение. - М.: Наука, 1964. - С. 412.
    5. Справочник по специальным функциям/Под ред. М. Абрамовича и И. Стриган. - М.: Наука, 1979. - С. 832.
    6. Зайцев А. Г. Объемные измерения зерен алмазных шлифовальных порошков марок АСВ и АСК, - Изв. вузов. Машиностроение, 1980, № 4, С. 146-148.
    7. Конструкционные материалы. - М.: Сов. эпцикл., 1964. - Т. 2, С. 408.
    8. А. с. 582957 (СССР). Способ изготовления абразивного инструмента / А. Г. Зайцев,- Опубл. в Б. И., 1977, № 45.
    9. А. с. 905040 (СССР). Способ изготовления алмазно-абразивного инструмента с ориентированным расположением зерен/А. Г. Зайцев, А. И. Скиданенко, Б. А. Меркушев. - Опубл. в Б. И., 1982, № 6.
    10. А. с. 906721 (СССР). Пресс-форма для изготовления абразивных инструментов с ориентированными зернами/А. Г. Зайцев, В. Д. Бондаренко, Б. А. Меркушев. - Опубл. в Б. И., 1982, № 7.