Рисунок 1 – Силы упругого последействия обработанной поверхности и силы на задней поверхности зуба инструмента

      Из рис. 1 видно, что движение зуба инструмента в направлении вектора скорости резания V будет возможно, когда сила Р, создаваемая силами упругого последействия Q обработанной поверхности будет больше проекции силы трения Fтр.

      Уравнение равновесия системы запишется в виде:

Fтр = Р = 0

где Fтр = Q • м • cosa; Р = Q • sina;
м – коэффициент трения между задней поверхностью зуба инструмента и обработанной поверхностью детали;
Q – сила упругопластического контакта, действующая на заднюю поверхность зуба;
sina – задний угол. После подстановки значений сил Fтр и P уравнение примет вид: Q • м • cosa = Q • sina

      После соответствующих преобразований уравнение примет вид:

м = tga

      Выполненные исследования показали, что коэффициент трения на задней поверхности зуба a = 0,6 [1], что соответствует величине заднего угла a = 31^o. Таким образом, движение зуба инструмента в направлении его вращения и противоположно действию тангенциальной составляющей силы Р возможно только при величине заднего угла a > 31^o.

      Учитывая, что для осевых инструментов типа зенкер и развертка величина задних углов не превышает 12^o, то движение вершины зуба, а соответственно, и центра инструмента противоположно действию силы Р, является невозможным.

      Траектория движения осевого инструмента при наличии колебательного движения рассмотрена на примере развертывания.

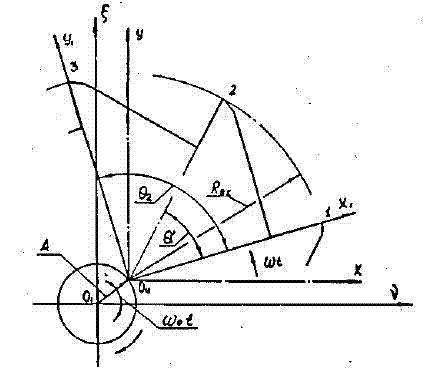
      Уравнение колебатсльного движения центра, когда его направление является противоположным направлению вращения развертки относительно неподвижной системы координат (рис. 2, а) имеющее общее начало с геометрической осью, предварительно обработанного отверстия, имеет:

vои = А•cos(w0•t);

Eои = –А•sin(w0•t);

где А – амплитуда радиальных колебаний центра развертки;
w0 – круговая частота колебаний центра развёртки.

      Предпологая, что период колебания центра определяется временем поворота развертки на один угловой шаг, с учетом уравнения (3) закон движения любого зуба развертки в плоскости, перпендикулярной её оси имеет вид:

vk = Rp • cos(w • t +Tetk) + A • cos(w • t);

Ek = Rp •sin(w • t +Tetk) – A • sin(w0 • t);

где Rp – радиус зуба развертки при эксцентричном расположении развертки относительно оси отверстия; w – круговая частота вращательного, движения развертки.

Рисунок 2 – Схема движения центра развертки:
а) направление движения центра противоположно направлению её вращения;
б) направление движения центра совпадает с направлением её вращения;

      Количество граней в поперечном сечении отверстия можно определить из равенства:

      Таким образом, количество граней при движении центра развертки в сторону, противоположную ее вращению, определится из выражения:

n = 2 • Z + 1

      Из него следует, что при движении центра развертки в сторону, противоположную ее вращению, количество граней в поперечном сечении отверстия – на единицу больше числа зубьев развертки.

      Создание условий, обеспечивающих движение центра развертки с задним углом a = 8^o, в сторону ее вращения, на практике не всегда представляется возможным. Например, для устранения эксцентричного расположения оси развертки относительно оси предварительно обработанного отверстия целесообразно применять "плавающее" закрепление развертки или детали. Устранение несоосности развертки и предварительно обработанного отверстия еще не гарантирует движение центра в направлении вращения развертки, так как при указанном закреплении развертки в период врезания силы демпфирования на вспомогательной режущей кромке практически отсутствуют. По мере входа развертки в обработанное отверстие силы демпфирования увеличиваются, но в это время на траекторию движения центра уже оказывает влияние след, образовавшийся в период врезания. Поэтому силы, действующие на задние поверхности зубьев, могут быть не достаточными для того, чтобы преодолеть сопротивление сил на передней поверхности и сил трения на задней поверхностизуба, а соответственно, и изменить направление движение центра в направлении вращения развертки.

      Увеличение сил упруго-пластического контакта на задней поверхности зубьев в момент врезания (рис. 2) создавалось искусственно, за счет пружины "плавающею" патрона, в котором крепится развертка.

      Уравнение колебательного движения центра, когда его направление совпадает с направлением вращения развертки относительно неподвижной системы координат (рис. 2,6), начало которой совпадает с геомстрической осью предварительно обработанного отверстия, имеет вид:

vои = А•cos(w0•t);

Eои = А•sin(w0•t);

      Траектория, описываемая зубьями развертки, когда движение центра совпадает с направлением ее вращения:

vk = Rp • cos(w • t +Tetk) + A • cos(w • t);

Ek = Rp •sin(w • t +Tetk) + A • sin(w0 • t);

      Тогда количество граней в поперечном сечении отверстия согласно выражению:

n = 2 • Z – 1

      Из выражения видно, что при совпадении направления движения центра и вращения развертки количество граней в поперечном сечении отверстия на единицу меньше числа зубьев.

      Выполненные исследования показали, что при отсутствии дополнительных источников сил на задней поверхности зуба осевого инструмента траектория колебательного движения зуба, а следовательно, и центра инструмента, противоположна направлению действия силы Р является невозможной.

СПИСОК ЛИТЕРАТУРЫ:

1. Малишко І.А. Основи теорії проектування осьових комбінованих інструментів, автореф. док. дис. – Київ, 1996. – 33 с.
2. Куликов В.А. Динамика станков. – M.: Машиностроение, 1967. – 360 с.