УДК 621.923
ВЛИЯНИЕ ХРУПКОГО РАЗРУШЕНИЯ МАТЕРИАЛА ПРИПУСКА КЕРАМИКИ НА ФОРМИРОВАНИЕ МИКРОРЕЛЬЕФА ПОВЕРХНОСТИ ДЕТАЛИ ПРИ АЛМАЗНОМ ШЛИФОВАНИИ
Гусев В.В., ДонНТУ, кафедра «Металлорежущие Станки и Инструмент», СартибаевД.Ю., магистран ДонНТУ
В статье рассмотрены физические основы формирования шераховатости поверхностного слоя деталей из керамики. Это позволило разработать математическую модель расчета параметров шераховатости керамики с учетом вероятностного характера хрупкого разрушения припуска в виде сколов.
Эксплуатационные показатели деталей, наряду с условиями работы (давления на сопрягаемых поверхностях, скорости их относительного перемещения, вида трения и смазки и т.д.) и параметрами, характеризующими состав, структуру и механические свойства взаимодействующих поверхностей, определяются параметрами, характеризующими состояние поверхностного слоя деталей, для оценки качества поверхностного слоя используют: геометрические параметры (отклонения от заданной геометрической формы, параметры волнистости, характеристики шероховатости, направление следов обработки). Из геометрических параметров детали наиболее изучено влияние на ее эксплуатационные показатели шероховатости поверхности, которая является простым и надежным критерием оценки состояния технологического процесса механической обработки и условий эксплуатации. Рекомендуемыми параметрами рабочих поверхностей деталей машин являются средне арифметическое отклонение профиля шероховатости Ra, высота сглаживания профиля с высоты небольшого выступа Rр, средний шаг неровностей профиля Sm, относительная опорная длина профиля tp и наибольшая высота профиля Rmax. Величина износа детали за период приработки зависит от того, насколько исходная шероховатость отличается от оптимальной, и может достигать 20-30% от предельного значения ее износа.
При обработке керамики наряду с внутрикристаллической деформацией протекает и межкристаллическая деформация — относительное скольжение и поворот зерен, дробление их на отдельные блоки, разрушение по границам зерен и их блоков. Примем, что формирование поверхностного слоя на керамической заготовке происходит з результате удаления материала припуска при копировании формы алмазного зерна круга и скола группы зерен керамики в виде очага разрушения. Независимо от вида керамики на обработанной поверхности наблюдается поле очагов разрушения в виде сколов, возникающее в результате случайного процесса разрушения припуска алмазными зернами (рис. 1). Для этого поля сколов характерно явление ординарности, так как они появляются по одиночке, а не по два, три, и т.д. Вероятность попадания того или иного числа сколов в плоскую фигуру не зависит от того, сколько сколов попало в любую другую непересекающуюся с ней фигуру. Таким образом, выполняется условие отсутствия взаимодействия сколов.

Рис. 1. Поверхность керамического образца после алмазного шлифования. Плоское шлифование периферией круга
1А1 250?20?32 АС6 125/100—4— М2-01
где Sc — площадь сколов на поверхности керамического образца площадью S. Исходя из сказанного, поле сколов может быть описано распределением Пуассона. Вероятность появления числа сколов m. (m = 1,2,3.) на базовой поверхности определяется по зависимости Поверхностная плотность образуемых сколов зависит от глубины резания и физико-механических свойств обрабатываемого материала (рис.2). С увеличением индекса хрупкости (Ну/К1с,) обрабатываемого материала, количество дефектов на единице поверхности уменьшается.
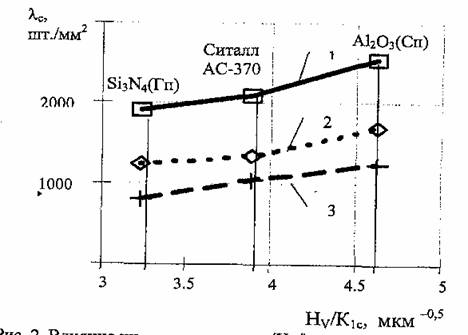
Рис. 2. Влияние индекса хрупкости (Нv/К1c) материала на поверхностную плотность сколов ?с при плоском врезном шлифовании алмазным кругом. 1А1 200?20?32 АС6 125/100— 4 - М2-0 1, скорость детали 0,5 м/мин, скорость круга 42 м/с, фактическая глубина резания: 1 — t=0,01 мм; 2—t=0,08 мм; 3— t=0,15 мм.
При переходе от числа сколов на поверхности к их числу на базовой длине в математической модели, на которой определяются параметры микрорельефа поверхностного слоя, использовали основное положение стереологии:
где SA — доля площади сколов на единице площади поверхности, LL — длина линейных отрезков пробной линии, пересекающей сколы, приходящяхся ма единицу длины этой линия, PP— число точек, попадающих на сколы, отнесенных к общему числу пробных точек.
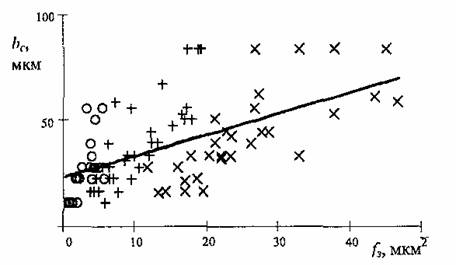
Обработка экспериментальных результатов показала наличие линейной корреляционной связи между средней шириной скола mb оксидной керамики и средними сечениями среза
Рис.3. Влияние среднего сечения среза на зернах f3 (мкм2) на ширину скола bc, (мкм)
O-Vд=0,5м/мин;+- Vд=2 м/мин; х – Vд =6 м/мин
В этом случае одномерный закон распределения элементарной случайной функции В(f3) нормален и имеет вид: Распространение разрушения вглубь керамики при очаговой форме разрушения h было принято равным половине размера ширины скола, т.е. h= 0,5-bc. Для определения количества сколов в i-том интервале необходимо найти обратное значение (квантили) распределения Пуассона. Используя ранее разработанную математическую модель и представленные выше положения хрупкого разрушения поверхности керамики при алмазном шлифовании, было произведено математическое моделирование процесса формирования шероховатости поверхности. Программа позволяет рассчитать параметры шероховатости в соответствии с ДСТУ ISO 12085-2001: средний шаг неровностей АR, среднюю глубину структурных элементов шероховатости R и максимальную глубину неровностей профиля Rx в пределах оценочной длины. Кроме этих параметров она позволяет рассчитать средне арифметическое отклонение профиля шероховатости Rа, высоту сглаживания профиля с высоты наибольшего выступа Rр и относителъную опорную длину профиля tp. При моделировании плоского шлифования периферией круга было установлено, что предложенная модель хрупкого разрушения поверхности керамики адекватно отражает реальный механизм образования шероховатости. Все теоретические значения укладываются в доверительный интервал экспериментальных данных. Рис. 4. Влияние глубины шлифования на среднюю глубину структурных элементов шероховатости R в пределах оценочной длины при плоском шлифовании периферией круга оксидной керамики. Таким образом, представленная модель хрупкого разрушения поверхности керамики при алмазном шлифовании адекватно отражает реальный механизм формирования шероховатости. данная модель реализована в универсальной математической системе расчетов MatCAD и может быть использована для прогнозирования всех параметров шероховатости обработанной поверхности керамических изделий при алмазном шлифовании (7) ЛИТЕРАТУРА 1. Гусев В.В. Молчанов А.Д. Математическая модель формирования шерахаватости поверхности конструкционной керамики при алмазном шлифовании // Прогрессивные технологии и системы машиностроения. Межд. сб. науч. трудов. Вып. 19. - Донецк: ДонГТУ, 2002. - С.50-57. 2. Гусев В.В. О распределении параметров срезов при глубинном круглом шлифовании периферией круга // Резание и инструмент в технологических системах: Межд. научн.-техн. сборник. - Харьков: НТУ ХПИ, 2003. -Вып. 65.- С.37-46.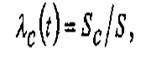
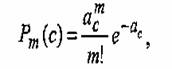
Это объясняется тем, что материалы с большим индексом хрупкости имеют меньшую предельную глубину микрорезания, при которой происходят переход от вязкого к хрупкому разрушению. При одной и той же глубине внедрения зерна и низком индексе хрупкости доминирует пластический механизм разрушения материала припуска, а с ростом индекса хрупкости материала происходит переход к хрупкому разрушению керамики. С увеличением фактической глубины резания при шлифования температура на поверхности заготовки увеличивается. заготовки увеличивается. Так как с ростом температуры твердость обрабатываемых материалов в зоне резания уменьшается, то индекс хрупкости материала уменьшается. Это приводят к увеличению доля пластических деформаций при разрушение материала припуска и снижению интенсивности сколов на поверхности заготовки.
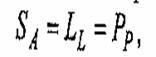
![]()
Следовательно, элементарная случайная функция имеет вид
![]()
где bc--случайная величина, распределенная нормально с параметрами
mb,, a — неслучайная величина, зависящая от физико-механических свойств обрабатываемой керамики.
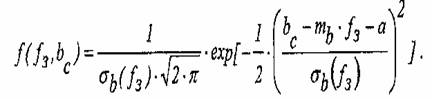
Таким образом, для определения условий съема материала припуска на первом этапе необходимо определить вероятность появления скола материала керамики при его срезании алмазным зерном. При наличии скола определяются его размеры. Для моделирования случайной дискретной величины, каковой является число сколов, нами был использован метод статистических испытаний (метод Монте-Карло). В математической модели, разработанной в работе, появление скола моделировалось по закону Пуассона. Глубина резания разбивалась на интервалы до 1 мкм.
Вероятность появления сколов определялась с помощью функции генерации случайных чисел по всем интервалам, сумма высоты которых составляет глубину резания. Эта задача решалась при использовании математического пакета MathCAD на ПЭВМ. Соответствующая функция — rnd(х). Таким образом, вероятность появления сколов в i-том интервале
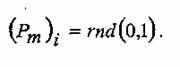
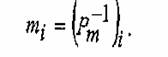
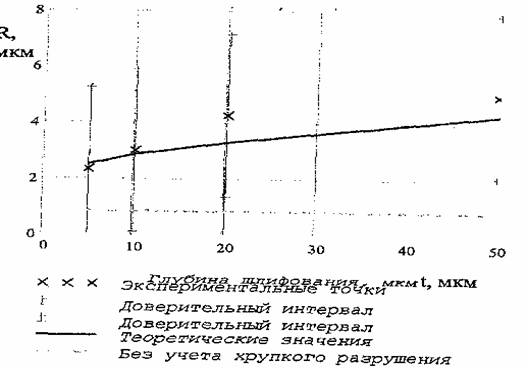
Круг 1А1 200?20?32 АС6 125/100—4— М2-01, скорость детали 6 м/мин, Скорость круга 42 м/с
3. Гусев В.В. Влияние на качество поверхностного слоя технической керамики износа алмазного шлифовального круга // Надежность инструмента и оптимизация технологических систем. Сборник научных работ. Вып. №12.- Краматорск: ДДМА, 2002.-С. 234-241.