Анализ диаграмм ускорений, рывка и усилий в шахтных подъёмных установках
Автор: Лазарева М.В.
Донецкий национальный технический университет
Источник: Х Международная научно-техническая конференция. Донецк 18-20 мая 2010 года. «Автоматизация технологических объектов и процессов. Поиск молодых»
Работа подъемной установки характеризуется цикличностью, т. е. рядом сменяющихся циклов, следующих друг за другом. В свою очередь каждый цикл можно разбить на четыре основ¬ных периода: разгон, равномерное движение, замедление до пол¬ной остановки и пауза.
Таким образом, чтобы обеспечить требуемую производитель¬ность любого подъема, каждый цикл должен укладываться в определенное, наперед заданное время. Для этого необходимо выдерживать расчетные значения ускорения и замедления, мак¬симальной скорости и продолжительности паузы, т. е. выдержи¬вать принятую диаграмму скорости. Диаграмма скорости подъ¬ема - это зависимость скорости движения подъемных сосудов от времени.
Подъемные установки в зависимости от назначение и высоты подъема, вида и грузоподъемности сосудов, числа обслуживаемых горизонтов, расстояния между ними могут работать по одной из следующих диаграмм движения (рис.1): а) трехпериодная, б) пятипериодная, в) шестипериодная, г) семипериодная.

Рисунок 1 - Диаграммы скорости шахтной подъемной машины: а — трехпериодная; б — пятипериодная; в — шестипериодная; г — семипериодная.
В зависимости от конструктивных особенностей ШПМ в процессе ее работы на ободе барабана (шкива трения) могут быть зафиксированы существенно разнящиеся величины движущих усилий (рис. 2).
Как видно из рисунка 2, движущие усилия изменяются ступенчато, причем в начале и конце движения возможно изменение знака. Такой характер диаграмм не является оптимальным, поскольку не учитывает динамические нагрузки в элементах привода и физиологическое воздействие рывка на пассажиров (горняков), находящихся в клети.
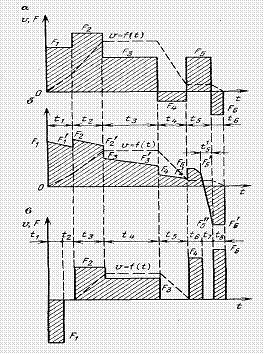
Рисунок 2 – Диаграммы усилий уравновешенной двухконцевой (а),
неуравновешенной с опрокидными скипами (б) и одноклетьевой (в)
подъемной установки.
Из анализа кривых следует, что наименьшее максимальное ускорение имеет место при работе по треугольной диаграмме, далее за ней следуют комбинированная, гармоническая, параболическая и циклоидальная диаграммы. Наибольший рывок наблюдается при работе по треугольной диаграмме. Наиболее равномерно рывок распределяется в гармонической и циклоидальной диаграммах.
Повышение плавности переходных процессов путем ограничения рывка желательно практически для всех подъемно-транспортных механизмов даже в тех случаях, когда правилами и нормами величина рывка не ограничивается. Это связано с желанием снизить динамические нагрузки рабочего оборудования и передач механизма в процессах пуска и торможения. Как было показано выше, ограничение темпа нарастания момента двигателя при пуске эффективно снижает амплитуды упругих колебаний. Соответственно снижаются максимальные нагрузки механического оборудования, повышается его надежность и долговечность. Кроме того, при ограничении рывка выбор зазоров в передачах происходит при меньших частотах вращения приводного двигателя, что также способствует снижению динамических нагрузок в элементах системы и привода.
В качестве примера рассмотрим моделирование системы в относительных единицах, тиристорный преобразователь – двигатель (ТП-Д) с ограничением рывка (рис.3). При моделировании системы были исследованы пуск, реверс, торможение, наброс и сброс нагрузки (рис.3).
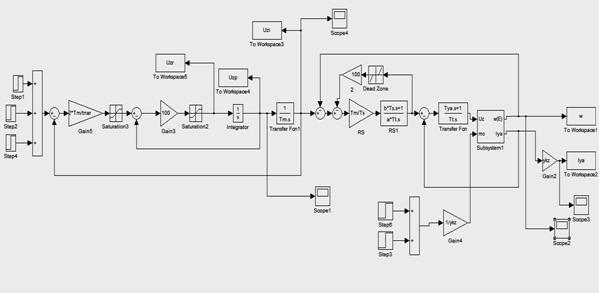
Рисунок 3 – Модель системы ТП-Д с ограничением рывка

Рисунок 4 – Переходные процессы, полученные при моделировании системы ТП-Д путём ограничения рывка
На основании выполненного анализа и результатов моделирования, можно сделать выводы о том, что система ТП-Д с ограничением рывка обладает лучшими показателями в плане формирования пускового режима, а также имеет место ограничения динамических нагрузок в системе с зазором, и имеет плавную характеристику изменения скорости.
Литература
- Малиновский А.К. Автоматизированный электропривод машин и установок шахт и рудников: учебн. пособие [для студентов высш. учебн. завед.] /Малиновский А.К. – М.: Недра,1987. – 280с.