Мариненко Олена Олександрівна
Электротехнічний факультет
Кафедра електропостачання міст
Спеціальність: Електротехнічні системи електропостачання
Тема випускної роботи: Оцінка надійності підстанції 110/10 кВ з урахуванням відновлення елементів системи, а також термінів діагностики засобів зіахисту
Керівник: Ковальов Олександр Петрович
Матеріали до теми випускної роботи:
Про автора
Реферат з теми випускної роботи
Актуальність.
Основним методом оцінки надійності структурно-складних схем в даний час є методи, засновані на складанні «схем мінімальних перерізів» [1]. Це означає, що принципову схему підстанції для оцінки її надійності потрібно представити в вигляді спеціальної схеми заміщення, що в багатьох випадках не є простим завданням. Тому розробка і використання нових способів перетворення складних за структурою схем систем електропостачання є актуальною науково-практичною задачею.
Наукова значимість.
Запропоновано удосконалений спосіб перетворення «трикутник - зірка» і «зірка - трикутник» для відновлюваних елементів мережі з урахуванням строків діагностики обладнання.
Мета роботи: Використовувати спосіб перетворення «трикутник - зірка» і «зірка - трикутник» і приведення складних за структурою схем до структур, що складається з послідовного і паралельного з'єднання елементів з урахуванням їх відновлення при відмовах.
Практична цінність. Запропоновано методику розрахунків надійності складних за структурою схем з урахуванням відновлення елементів, точність яких не відрізняється від методики, запропонованої в [1] більше, ніж на 5%.
Стан питання. На сьогоднішній день для оцінки надійності складних за структурою схем використовуються методи розрахунків, засновані на складанні схем мінімальних перерізів, тобто схем, що складаються з послідовно з'єднаних паралельних груп. Кожен елемент групи характеризується своїм параметром
 - параметр потоку відмов і відновлень відповідно
- параметр потоку відмов і відновлень відповідно
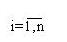 .
Для простих схем заміщення, що складаються з послідовного, паралельного або змішаного з'єднання елементів, еквівалентні параметри потоків відмов і відновлень відповідно
.
Для простих схем заміщення, що складаються з послідовного, паралельного або змішаного з'єднання елементів, еквівалентні параметри потоків відмов і відновлень відповідно
 знаходим наступним чином [4]:
знаходим наступним чином [4]:
1. Послідовне з'єднання:
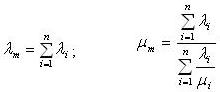
2.Паралельне з'єднання:

Формули (1) і (2) справедливі, коли функціонування елемента системи можна описати за допомогою чергуються інтервалів часу роботи:
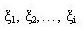 й пробою
й пробою  .
Випадкові інтервали часу
.
Випадкові інтервали часу и
и 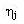 не суперечать експоненційної функції розподілу, тобто
не суперечать експоненційної функції розподілу, тобто
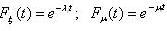 Всі розміри
Всі розміри  та
та 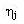 взаємно незалежні і виконується умова:
взаємно незалежні і виконується умова:


Рис. 1 - Можлива реалізація електроустаткування
Результати дослідження.
Схеми заміщення системи електропостачання не завжди складаються з послідовного, паралельного або змішаного з'єднання елементів. Існують і більш складні схеми - місткові [1]. Під системою електропостачання зі складною схемою будемо розуміти таку схему, до складу якої входять хоча б одна група елементів, що мають мостикову схему.
Для таких схем пропонується використовувати спосіб перетворення «трикутник - зірка». Цей спосіб відрізняється від відомого [5] тим, що дозволяє виробляти перетворення складних схем заміщення з урахуванням відновлення елементів і термінів їх діагностики.
Сутність пропонованого перетворення «трикутник - зірка» полягає в тому, що з'єднання елементів у вигляді трикутника замінюється еквівалентним по надійності з'єднанням
у вигляді зірки, тобто задача зводиться до визначення еквівалентних інтенсивностей відмов і відновлень «зірки», через аналогічні параметри надійності «трикутника».
На рис. 2. a, б зображено дві схеми з'єднання елементів - трикутник і зірка. Нехай кожен елемент трикутника має інтенсивності відмов
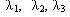 і відновлень
і відновлень 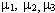 Аналогічні параметри надійності має і зірка
Аналогічні параметри надійності має і зірка
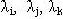 і відновлень
і відновлень
 .
.
Наведені структури будуть еквівалентними по надійності, якщо інтенсивності відмов і відновлень між вузлами 1-3, 1-2, 2-3 трикутника будуть рівні інтенсивності відмов і відновлень між відповідними вузлами зірки. Між вузлами 1-3 трикутника один шлях проходить через елемент 1, а другий - через елементи 2 і 3. Для вузлів
1-3 зірки є тільки один шлях через елементи і і k. Схеми заміщення наведені на рис. 2. в. Аналогічним чином складаються схеми заміщення і для шляхів 1-2 і 2-3 трикутника і зірки (рис. 2. г, д).
Використовуючи отримані схеми заміщення, за допомогою формул (1), (2) визначаються еквівалентні інтенсивності відмов і відновлень для всіх шляхів успішного функціонування елементів трикутника і зірки. Прирівнявши відповідні інтенсивності відмов і відновлень шляхів успішного функціонування елементів трикутника і зірки, отримаємо систему з шести лінійних алгебраїчних рівнянь:

Висловивши інтенсивності відмов
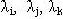 і відновлень
і відновлень
 елементів зірки через інтенсивності відмов і відновлень елементів трикутника, отримаємо:
елементів зірки через інтенсивності відмов і відновлень елементів трикутника, отримаємо:
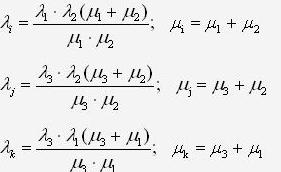
Якщо потрібно зворотний перехід від зірки до труегольніку, то, використовуючи цю ж систему рівнянь (3), отримаємо:

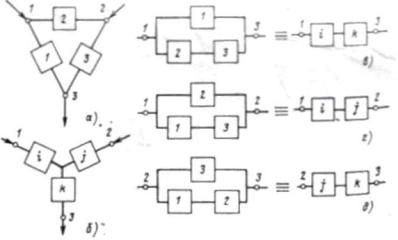
Рис.2 - Схемы зірки та трикутниика
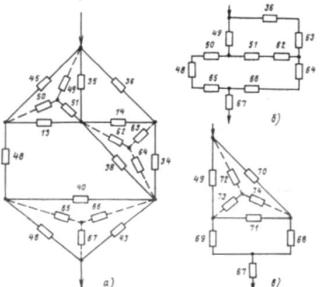
Рис.3 - Показники надійності схеми
Розрахунок надійності складних схем систем електропостачання
з урахуванням відновлення елементів і з застосуванням перетворення «трикутник - зірка» менш трудомісткий порівняно
з застосовуваними в даний час методами, які вимагають складання спеціальних схем заміщення мінімальних перерізів.
Висновки:
1. Запропоновано новий варіант перетворення з'єднання елементів у вигляді трикутника в еквівалентний за надійності з'єднання елементів у вигляді зірки з урахуванням відновлення елементів, що дозволяє приводити складні містково схеми до простих послідовно-паралельним.
2. На основі запропонованого перетворення розроблена
методика розрахунку надійності складних схем відновлюваних
систем електропостачання, що відрізняється від існуючих тим,
що не вимагає складання логічної схеми заміщення мінімальних перерізів. В якості розрахункової використовується принципова схема електропостачання.
3. Точність пропонованої методики не поступається існуючим [1, 2, 3].
При написанні даного реферату магістерська робота не завершена. Остаточний варіант роботи можна отримати у автора або наукового керівника після грудня 2010 року.
Література
1. Рябинин И. А. Основы теории и расчета надежности судовых электроэнергетических систем. — 2-е изд. Л.: Судостроение. 1971, с. 58-62.
2. Константинов Б. А., Лосев Э. А. Логико-аналитический метод расчета надежности восстанавливаемых систем электроснабжения. — Электричество, 1971, № 12, с.15-17.
3. Фокин Ю. А., Чан Динь Лонг. Структурный анализ и методы оценки надежности сложных систем электроснабжения. — Электричество, 1973. № 5, с. 4-6.
4. Козлов Ю. А., Ушаков И. А. Справочник по расчету надежности аппаратуры радиоэлектроники и автоматики.— М.:
Советское радио, 1975, с. 105-107.
5. Голинкевич Т. А. Прикладная теория надежности.—
М.: Высшая школа, 1977, с. 1-8.
6. Зорин В. В., Тисленко В. В., Клеппель Ф. и др. Надежность систем электроснабжения. Киев: Высшая школа, 1984, с. 207-217.
7. Фабрикант В.П. О применении теории надежности к оценке устройств релейной защиты. – Электричество, 1965, №9, с. 36-40.
8. Синьчугов Ф.И. Основные положения расчета надежности
электроэнергетических систем. – Электричество, 1980, № 4, с. 12-16.
9. Ковалев А.П., Муха В.П., Шевченко О. А., Якимишина В.В.
Метод расчета надежности электроснабжения узлов нагрузки с учетом отказов в срабатывании защитных коммутационных аппаратов.
Источник: Наукові праці Донецького державного технічного університету. Серія: «Електротехніка і енергетика», випуск 41: Донецьк: ДонДТУ, 2002. - с. 107-113.
Про автора
 - параметр потоку відмов і відновлень відповідно
- параметр потоку відмов і відновлень відповідно
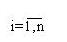 .
Для простих схем заміщення, що складаються з послідовного, паралельного або змішаного з'єднання елементів, еквівалентні параметри потоків відмов і відновлень відповідно
.
Для простих схем заміщення, що складаються з послідовного, паралельного або змішаного з'єднання елементів, еквівалентні параметри потоків відмов і відновлень відповідно
 знаходим наступним чином [4]:
знаходим наступним чином [4]:

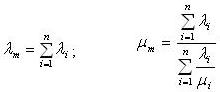

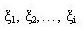 й пробою
й пробою  .
Випадкові інтервали часу
.
Випадкові інтервали часу и
и 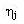 не суперечать експоненційної функції розподілу, тобто
не суперечать експоненційної функції розподілу, тобто
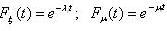 Всі розміри
Всі розміри 

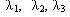 і відновлень
і відновлень 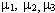 Аналогічні параметри надійності має і зірка
Аналогічні параметри надійності має і зірка
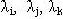 і відновлень
і відновлень
 .
.