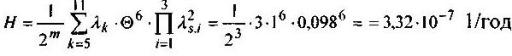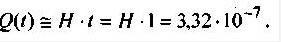Оценка вероятности появления цепочечных аварий в энергосистемах
Ковалев А.П., Чурсинов В.И., Якимишина В.В.
Источник: Наукові праці Донецького національного університету. Серія: «Електротехніка і енергетика», випуск 67, Донецьк: ДонНТУ, 2004. - 204с.
Введение. Толчком к развитию методов оценки и прогнозирования цепочечных аварий в энергосистемах (ЭС) послужила авария, случившаяся 9 ноября 1965 года в США, которая привела к тому, что на территории с населением около 30 млн. человек более чем на 10 часов была прекращена подача электроэнергии.
Ущерб от аварии составил более 100 млн. долларов. Последовавшие после этого десяток мелких (с экономической точки зрения), но подобных аварий по стране завершились 13 июля 1977 года аварией в Нью-Йорке. В течение 25 часов была парализована жизнь Нью-Йорка. Ущерб от последствий этой аварии составил более 1 млрд. долларов [1,2]. Спустя 26 лет, 14 августа 2003 года в 16 часов 11 минут по местному времени из-за повреждения на линии Ниагара-Мохок без электричества осталась почти вся восточная часть Северной Америки, т.е. 50 млн. человек [3].
О каждой из перечисленных аварий можно сказать, что данная энергосистема потеряла живучесть. Под живучестью будем понимать свойства объекта противостоять возмущениям, не допуская их каскадного развития с массовым нарушением питания потребителей [4].
Живучесть электроэнергетической системы (ЭЭС) зависит от ее структуры, конфигурации, надежности электрооборудования, средств релейной защиты и противоаварийной автоматики, а также от квалификации обслуживающего персонала, запаса устойчивости, резерва активной мощности и т.д. [5].
При эксплуатации ЭЭС наблюдается появление так называемых цепочечных аварий из-за последовательного отказа в срабатывании нескольких выключателей при отключении повреждений [6].
Цепочечные аварии наблюдались в 25 ЭЭС и двух ОЭС бывшего СССР. За 5 лет было зафиксировано 75 цепочечных аварий. В 81% случаев цепочечные аварии происходили из-за повреждений в сети и отказа в функционировании защитных коммутационных аппаратов [7]. На цепочечные аварии приходится 90% народнохозяйственного ущерба [9].
Под глубиной цепочной аварии понимается уровень расстройства функционирования установок энергосистемы при авариях и нарушениях в работе [6,7,8].
Показателем живучести может служить частота появления системных цепочечных аварий с различной глубиной нарушения электроснабжения [7].
Цель: oценить частоту (вероятность) появления цепочечных аварий при эксплуатации ЭЭС.
Материал и результаты исследований. В настоящей работе предлагается формула для определения частоты (вероятности) появления в ЭЭС цепочечных аварий, которые могут происходить при коротком замыкании (КЗ) в защищаемом элементе сети и отказе в срабатывании ряда защитных коммутационных аппаратов, через которые прошел сквозной аварийный ток:
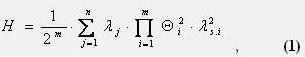
где
 - параметр потока КЗ в j-том элементе сети;
- параметр потока КЗ в j-том элементе сети;
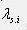 - параметр потока отказов в срабатывании i-того защитного коммутационного аппарата. Здесь индекс s указывает на то, что учитывается поток отказов в срабатывании j-того защитного коммутационного аппарата;
- параметр потока отказов в срабатывании i-того защитного коммутационного аппарата. Здесь индекс s указывает на то, что учитывается поток отказов в срабатывании j-того защитного коммутационного аппарата;
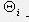 - интервал времени между профилактическими осмотрами системы отключения i-того защитного коммутационного аппарата вместе с его релейной защитой;
- интервал времени между профилактическими осмотрами системы отключения i-того защитного коммутационного аппарата вместе с его релейной защитой;
m - число защитных коммутационных аппаратов, через которые прошел сквозной аварийный ток, при этом действие их основной или резервной релейной защиты обязательно.
Формула (1) справедлива при выполнении условия: интервалы времени между появлениями КЗ в элементе сети и интервалы времени между отказами в срабатывании защитных коммутационных аппаратов не противоречат экспоненциальным функциям распределения вероятностей с параметрами соответственно
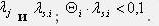
При выводе формулы (1) были приняты следующие допущения: устройства защиты могут выходить из строя только тогда, когда они находятся в режиме ожидания. Если к моменту возникновения повреждения в сети, на которое должна реагировать релейная защита, она находилась в исправном состоянии, то маловероятно, чтобы защита вышла из строя, находясь в режиме тревоги [10].
Отказы в схемах РЗ и приводе выключателя выявляются и устраняются только в результате профилактических проверок. Предполагается, что проверки РЗ и привода выключателя абсолютно надежные.
Под отказом в срабатывании защитного коммутационного аппарата будем понимать тот из них, который приводит к отказу в отключении поврежденного элемента сети при КЗ в зоне действия его релейной защиты.
В том случае, если сроки профилактики систем отключения защитных коммутационных аппаратов будут одинаковы, тогда формула (1) примет вид:
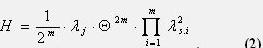
Вероятность появления каскадной аварии Q(t) в течение времени t можно определить следующим образом:
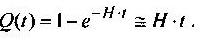
В том случае, если H*t < 0,1.
Пример. Для схемы, представленной на рисунке 1 определить вероятность аварийного отключения секций шин I и II в течение года при КЗ в одном из элементов сети, получающих электроэнергию от секции шин I.
Дано:
 =3 1/год,
где
=3 1/год,
где
 - параметр потока КЗ в элементах сети, получающих электроэнергию от секции I;
- параметр потока КЗ в элементах сети, получающих электроэнергию от секции I;
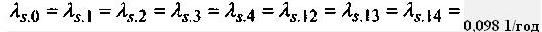 -
параметр потока отказов в срабатывании защитного коммутационного аппарата;
-
параметр потока отказов в срабатывании защитного коммутационного аппарата;
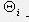 год — интервал времени между профилактическими осмотрами системы отключения защитного коммутационного аппарата вместе с устройством релейной защиты.
год — интервал времени между профилактическими осмотрами системы отключения защитного коммутационного аппарата вместе с устройством релейной защиты.
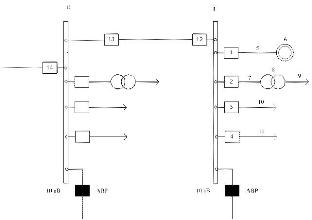
Рисунок 1 - Схема электроснабжения секций шин I и II
Решение. При КЗ в одном из k, k=5,11 элементов (рис. 1) в действие приходят релейные защиты коммутационных аппаратов 14, 13, 12 и одного из коммутационных аппаратов отходящих от секции шин I линий (1 или 2, или 3, или 4).
Отключение секций I и II коммутационным аппаратом 14 произойдет при случайном появлении КЗ в одном из k элементов сети; при этом откажет в срабатывании ближайший к месту КЗ коммутационный аппарат, через который прошел сквозной аварийный ток, а также откажут в срабатывании аппараты 12 и 13.
Используя формулу (2) при m=3, находим:
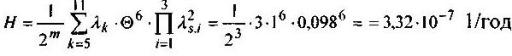
Вероятность аварийного отключения в течение 1 года секций шин I и II при КЗ в одном из k элементов сети, получающих электроэнергию от секции I, находим, пользуясь формулой (3). Поскольку H*t <<0,1, то получим:
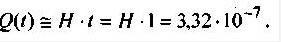
Вывод.
Результат расчета показал, что если под наблюдением в течение 1 года будет находиться N = 3*106 систем электроснабжения, аналогичных изображенной на рис. 1, суммарный параметр потока КЗ в электрооборудовании и линиях, получающих электроэнергию от секции I, будет равен 3 1/год, а параметр потока отказов в срабатывании защитных коммутационных аппаратов будет 0,098 1/год, то в течение года статистически произойдет такое КЗ, в результате которого аварийно отключатся секции шин I и П.
Литература
1. Китушин В.Г. Надежность энергетических систем. М: Высш.шк., 1984. - 256 с.
2. Prevention of power failures Vol. 3 Studies of the task groups on the northeast power interruption. Areport to the federal power commission. June 1967, 142 p.
3. Надежность систем энергетики. Терминология.М.: Наука, 1980. - Вып.95. - 44с.
4. Руденко Ю.Н., Ушаков И.А. Надежность систем энергетики. М.: Наука, 1986. - 276 с.
5. Китушин В.Г. Определение характеристик отказов системы при цепочечном развитииаварий. - Изв. АНСССР. Энергетика и транспорт, 1977, №3, c. 20-30.
6. Гук Ю.Б. Теория надежности в электроэнергетике: Учеб. пособие для вузов. - Л.: Энергоатомиздат, 1990. - 208 с.
7. Розанов М.Н. Надежность электроэнергетических систем.-М.: Энергоатомиздат, 1984.- 176с.
8. Гук Ю.Б. Анализ надежности электроэнергетических установок - Л.: Энергоатомиздат. Ленинградское отделение, 1988. - 224 с.
9. Фабрикант В.П. О применении теории надежности к оценке устройств релейной зашиты. - Электричество, 1965, №9, c. 36 - 40.
10. Эндрени Дж. Моделирование при расчетах надежности в электроэнергетических системах: Пер. с англ./Под ред. Ю.И. Руденко-М.: Энергоатомиздат, 1983. - 336 с.
Библиотека
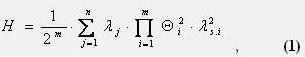
 - параметр потока КЗ в j-том элементе сети;
- параметр потока КЗ в j-том элементе сети; 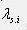 - параметр потока отказов в срабатывании i-того защитного коммутационного аппарата. Здесь индекс s указывает на то, что учитывается поток отказов в срабатывании j-того защитного коммутационного аппарата;
- параметр потока отказов в срабатывании i-того защитного коммутационного аппарата. Здесь индекс s указывает на то, что учитывается поток отказов в срабатывании j-того защитного коммутационного аппарата; 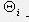 - интервал времени между профилактическими осмотрами системы отключения i-того защитного коммутационного аппарата вместе с его релейной защитой;
- интервал времени между профилактическими осмотрами системы отключения i-того защитного коммутационного аппарата вместе с его релейной защитой; 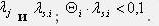
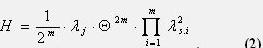
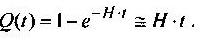
 - параметр потока КЗ в элементах сети, получающих электроэнергию от секции I;
- параметр потока КЗ в элементах сети, получающих электроэнергию от секции I;
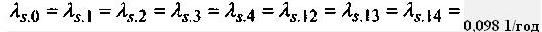 -
параметр потока отказов в срабатывании защитного коммутационного аппарата;
-
параметр потока отказов в срабатывании защитного коммутационного аппарата;