ОПРЕДЕЛЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ПАРАМЕТРОВ ОБМОТКИ ВОЗБУЖДЕНИЯ СИНХРОННОГО ГЕНЕРАТОРА ИЗ ОПЫТОВ ВНЕЗАПНОГО ТРЕХФАЗНОГО КОРОТКОГО ЗАМЫКАНИЯ
Ларин А.М., к.т.н., доц., Ткаченко А.А., аспирант, Ларина И.И., к.т.н., доц.
Донецкий национальный технический университет
Украина, 83000, Донецк, ул. Артема, 58, ДонНТУ, кафедра "Электрические системы"
Викладені основні положення методу експериментального визначення електромагнітних параметрів обмотки збудження синхронних машин. Метод засновано на дослідних даних, які реєструються при раптових трифазних коротких замиканнях на затисках електричної машини. Наведені результати досліджень для явнополюсного синхронного генератора типу СГ-18,75 та турбогенератора ТВВ-160.
Изложены основные положения метода экспериментального определения электромагнитных параметров обмотки возбуждения синхронных машин. Метод основан на опытных данных, регистрируемых при внезапных трехфазных коротких замыканиях на выводах электрической машины. Приводятся результаты исследований для явнополюсного синхронного генератора типа СГ-18,75 и турбогенератора ТВВ-160.
ВВЕДЕНИЕ
Достоверность расчетов переходных процессов (ПП) в синхронных машинах (СМ) определяется точностью задания их математической модели. Модель СМ в виде общепринятой Т-образной схемы замещения приводит к большим погрешностям при расчете тока в обмотке возбуждения генераторов (ОВГ) при моделировании по уравнениям Парка-Горева [1]. Представление ОВГ самостоятельной многоконтурной схемой [2] также не обеспечивает достаточную точность расчетов. Существенная погрешность объясняется, в частности, неучетом взаимоиндукции между обмоткой возбуждения и демпферными контурами [3]. Наиболее точную и полную информацию о совокупности электромагнитных параметров СМ дают частотные характеристики (ЧХ). Они позволяют достаточно точно учесть все особенности СМ при расчете ПП, не вникая в структуру взаимосвязей отдельных элементов. Целью настоящей работы является обоснование необходимой структуры схемы замещения и разработка способа определения электромагнитных параметров обмотки возбуждения СМ для повышения точности расчетов токов в ОВГ при трехфазных коротких замыканиях.
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ СООТНОШЕНИЯ
Предлагаемый способ основан на разработанном в [4] методе определения тока в обмотке возбуждения СМ при трехфазных коротких замыканиях. В соответсвии с этим методом операторное выражения апериодической составляющей тока ОВГ ifan(p) при трехфазном коротком замыкании определяется по известному операторному коэффициенту распределения тока статора в ветви обмотки возбуждения Cf(p) и операторной проводимости по продольной оси СМ со стороны обмотки статора yd(p) следующим образом:
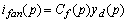 .(1)
.(1)Следовательно, зная операторные значения проводимости yd(p) и составляющей тока ротора ifan(p) , можно определить операторный коэффициент Cf(p):
 .(2)
.(2)На основании свойств преобразования Лапласа и интеграла Фурье после подстановки p=js получим выражение для определения частотной характеристики коэффициента распределения периодического тока статора в ветви ОВГ:
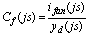 .(3)
.(3)Для перехода в частотную область в измеренном токе в обмотке возбуждения выделяется апериодическая составляющая, которая аппроксимируется следующим соотношением:
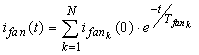 ,(4)
,(4) где ifank(0), Tfank
— начальные значения и постоянные времени затухания k-ой
экспоненциальной составляющей апериодического тока ОВГ; N —
количество контуров на роторе.
Такому закону изменения апериодического
тока ОВГ во времени соответствует следующее выражение для определения
его изменения в частотной области ifan(p)
 .(5)
.(5)С другой стороны для схемы замещения общепринятого типа, приведенной на рис.1, частотная характеристика Cf(js) может быть рассчитана по ее параметрам следующим образом:
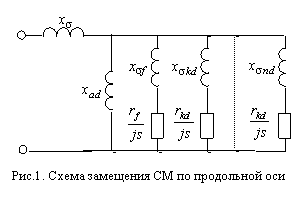 ,(6)
,(6)где yf(js); — ЧХ проводимости контура обмотки возбуждения; yad(js) — ЧХ проводимости СМ, измеренная относительно зажимов ветви намагничивания.
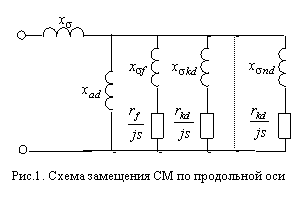
 ,(7)
,(7)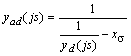 .(8)
.(8)Следовательно, определив по (3) с учетом (4) по данным опыта трехфазного короткого замыкания частотную характеристику Cf(js) и зная характеристику yad(js) можно вычислить частотную характеристику проводимости контура ОВГ:
 .(9)
.(9)В соответствии с (7) определяются активное и индуктивное сопротивление рассеяния обмотки возбуждения для схемы замещения, приведенной на рис.1:
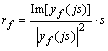 ;
; 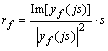 .(10)
.(10) В соответствии с
предложенным подходом были выполнены исследования для ряда
турбогенераторов путем математического моделирования по
дифференциальным уравнениям Парка-Горева. Синхронные машины
представлялись многоконтурными схемами замещения с постоянной
взаимоиндукцией (рис.1). Анализ полученных результатов указывает на
практичеcки полное совпадение исходных значений параметров ОВГ с
расчитанными по предложенной методике. Это подтверждает достоверность
разработанного алгоритма для общеприняой схемы замещения.
Экспериментальная проверка осуществлялась
по данным опытов внезапного трехфазного короткого замыкания на выводах
синхронного генератора СГ-18,75 и турбогенератора типа ТВВ-160. Опыты
проводились при начальных значениях напряжения, соответствующих
ненасыщенным параметрам ЭМ.
Генератор СГ-18,75 (Sном = 18,57 кВА; Uном = 230 В; Iном
= 47 А; n = 1000 об/мин.) является явнополюсной ЭМ без демпферных
контуров, имеющей весьма малый междужелезный зазор под полюсами.
Значения индуктивного сопротивления рассеяния xσ обмотки статора принималось равным 0,04098 о.е. В результате были получены следующие значения параметров ОВГ: yf = 0,00131 о.е., yσf
= 0,102 о.е. По полученным параметрам схемы замещения рассчитывался ток
в ОВГ при внезапном трехфазном коротком замыкании (рис.2, сплошная
кривая).

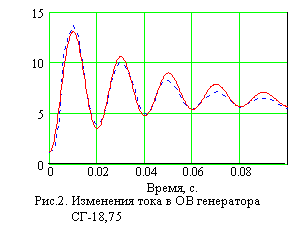
Сопоставление результатов
расчета с исходными экпериментальными данными (рис.2, штриховая кривая)
указывает об их удовлетворительном совпадении. Максимальная погрешность
не превышает 9,5%. Это свидетельствует о том, что схема замещения,
представленная на рис.1 адекватно отражает динамические свойства
синхронной машины без демпферных обмоток.
Частотная характеристика Cf(js)
для турбогенератора ТВВ-160, полученная экспериментально по соотношению
(3), и рассчитанная по параметрам обмотки возбуждения в соответствии с
описанной методикой для схемы замещения с постоянной взаимоиндукцией
между обмотками ЭМ, существенно отличаются. Отличия расчетной и
экспериментальной зависимостей превышают 32% в области скольжений от
0,1 до 1,0 о.е. по действительной и мнимой составляющим, погрешность по
амплитудным значениям комплексов несколько ниже (25%).
На рис.3 приведены зависимости изменения
тока в обмотке возбуждения при КЗ на выводах турбогенератора ТВВ-160.
Использование схемы замещения,
представленной на рис.1 приводит к существенным погрешностям в
определении тока в обмотке возбуждения при КЗ. Экспериментальная
зависимость (кривая 1) не совпадает с результатами расчета по уравненям
Парка-Горева более чем на 27,9%. Это подтверждает необходимость
использования для моделирования схем замещения уточненной структуры.
Рассмотрим возможность определения
электромагнитных параметров обмотки возбуждения предложенным методом
применительно к схеме замещения с различной взаимной индуктивностью
между обмоткой возбуждения и эквивалентным демпферным контуром.
Массивные элементы ротора турбогенератора представим в такой схеме
замещения одним эквивалентным демпферным контуром с параметрами xσD, rD(рис.4).
Частотная характеристика коэффициента участия тока статора в ветви обмотки возбуждения Cf(js) может быть рассчитана по параметрам уточненной схемы замещения следующим образом:
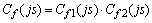 ,(11)
,(11)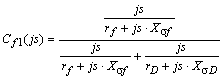 ,(12)
,(12)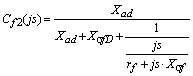 ,(13)
,(13)

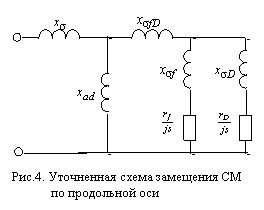
Индуктивное сопротивление взаимоиндукции между обмоткой возбуждения и эквивалентным демпферным контуром xσfD и электромагнитные параметры обмотки возбуждения yf, xσf для схемы замещения представленной на рис.4 должны определяться из условия минимального отличия частотных характеристик Cf(js) полученных экспериментально по (3) и расчетным путем по (11)-(13). Частотная характеристика проводимости yd(js)
со стороны обмотки статора ЭМ не должна изменяться для различных
параметров роторных контуров. Для осуществления указанной процедуры
может быть использованна методика расчета параметров контуров,
изложенная в [5].
Выполненные для турбогенератора ТВВ-160
исследования позволили получить следующие значения искомых параметров
(о.е.): xσfD = -0,012; xσf = 0,151; yf = 0,00141.
В этом случае отличие рассчитанной по (11)-(13) ЧХ Cf(js)
от экспериментальной зависимости значительно уменьшилось по сравнению с
использованием общепринятой схемы замещения. Погрешность по
действительной составляющей и амплитудному значению снизилась до 10%.
Соответствующее повышение точности расчета переходных процессов
наблюдается и во временной области (рис.3,кривая 3). Отличие
рассчитанного тока в обмотке возбуждения от экспериментальной
зависимости не превышает 8,1%.
ВЫВОД
Предложенный способ позволяет по данным опытов внезапного трехфазного короткого замыкания на выводах синхронного генератора определять электромагнитные параметры цепи обмотки возбуждения для схем замещения общепринятой и уточненной структуры.
ЛИТЕРАТУРА:
[1] Казовский , Рогозин
Г.Г., Горин В.Я. Исследование частотных характеристик турбогенераторов
// Электротехника 1975 №1.
[2] Сидельников . Синтез схемы замещения
СМ при представлении обмотки возбуждения многоконтурной схемой. //
Электрические машины. 1983 №7.
[3] Canay M. Experimentelle ermittluhg
der ersataschemata und der parameter liner idealisierten
synchromaschine. // Bull des schwezerischen electrotechnischen Vereins.
1972.
[4] Ларин А.М., Ларина И.И., Гуедиди
Фаузи. Упрощенная модель синхронной машины для расчета трехфазных
коротких замыканий с учетом многоконтурности и несимметрии ротора.
Научные труды ДонГТУ, серия Электротехника и энергетика, вып.4. Донецк,
1999. — С. 60-64.
[5] Рогозин Г.Г., Ларин А.М. Расчет
параметров эквивалентных роторных контуров синхронных машин по их
экспериментальным частотным характеристикам. — С. 60-64.