Постоянный магнит синхронных двигателей (ПМСД). Параметры влияющие на
процесс синхронизации ПСДМ.
Авторы: J. Rais, M. P. Donsiоn; Аннотация.
Эта работа является решением проблем о ПСДМ.
В первой части есть расчеты и принцип работы,
дизайн ПСДМ. Ниже приводится математическая модель
ПСДМ, которая используется при расчете поведения ПСДМ.
Третья часть описывает влияние на параметры
переходного процесса, особенно его начала и
процесса синхронизации. В последней части отмечаем,
как параметры влияют на компьютере с помощью
тренажер программы PCSIM. Есть 4 случая. Первый
случай: источник напряжения инвертора применяется к ПСДМ,
второй случай: источник напряжения инвертора контролируемых
широтно-импульсных модуляций применяется к ПСДМ, третий:
источник напряжения инвертора с питающего кабеля применяется к
ПСДМ и последний случай – влияние качества
поставляемого электричества на поведение ПСДМ.
Ключевые слова.
Постоянный магнит, синхронный двигатель, модели
электромагнитного момента, источник напряжения инвертора.
Ключевые слова.
Постоянный магнит, синхронный двигатель, DQ модели
электромагнитного момента, источник напряжения инвертора.
1.
Введение.
Постоянный магнит синхронных двигателей
Имеет повышенное применение в нескольких областях, таких как сцепление
автомобилей, робототехники и аэрокосмических технологий.
Плотность мощности постоянного магнита синхронного двигателя
выше, чем одного асинхронного двигателя с теми же
параметрами, в связи с
магнитным производством поля статора. В настоящее время постоянными магнитами
синхронных двигателей не только более
мощный, но и с меньшей массой и с более низким моментом
инерции.
Мы не можем использовать типичные модели DQ. Эта модель линейная и с постоянными параметрами, применительно к
основным полюсам синхронных машин. Этого может быть недостаточно
для точного моделирования характеристик прогнозирования
постоянных магнитов синхронных двигателей внутреннего типа. Приводит к серьезным ошибкам, когда мы оцениваем
производительность машины или расчета цепей управления.
Поведение постоянных магнитов
двигателей внутреннего типа может весьма отличаться от
ожидаемого, используя традиционные две оси теории. Поэтому необходимо создание новых моделей для этого случая. Мы должны
учесть перераспределение магнитного потока вдоль
ротора между магнитами и воздушным
зазором. Должны учитывать необходимые точности из
результаты также надежность процедуры тестирования для
определение параметров машины, когда мы
разрабатываем постоянные магниты модели двигателя.
Обычные методы испытаний для определения
синхронных параметров машины не могут быть применены в
машине с постоянным магнитом. И вот почему
мы используем тестовые процедуры, которые отличаются от
классических методов.
2.
DQ модель ПМСД.
На рисунке 1 изображена схема замещения
синхронного электродвигателя с постоянным магнитом в
роторе. Это схема одной фазы, где активное сопротивление одной из фаз в обмотке статора Rs, а ииндуктивное
Ls. Когда ротор вращается, его постоянный
магнит создает магнитное поле с магнитным потоком Фf,
Таким образом, электрическое напряжение индуцирует в обмотке статора Ue. Но
напряжение имеет противоположное значение напряжению питания Us.
Перевод: Очеретная В.В.
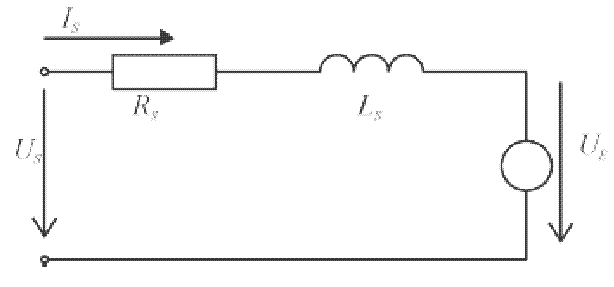
Рисунок - 1 Схема замещения ПСДМ
Мы можем вывести эту модель из общей модели
синхронных двигателей, в которой мы принимаем небольшое допущение.
Мы пойдем от схемы замещения изображённой на рисунке 1.
Причины, понижающие допущение:
- напряжение питания имеет гармонической волны;
- значения обмотки статора R и L являются одинаковыми для
всей обмотки и остаются постоянными;
- направление магнитной индукции B является постоянной
воздушного зазора;
- магнитный поток линейный и потери в ли не учитываются;
- наведенное напряжение Ui имеет гармонические волны.
Уравнения для электрической цепи:
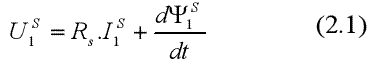
где верхний индекс S меняется в системе координат статора. Теперь мы можем определить сочетание магнитного потока:

magnetic flux ?F is excited by permanent magnets in rotor and it transforms to stator coordinates. Both equations are transformed to coordinate system DQ, which is rotating same radian frequency like rotate magnetic field:

Теперь мы можем написать уравнение в виде DQ:
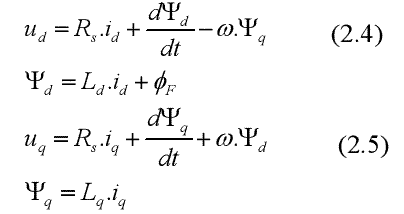
Потокосцепление статора:
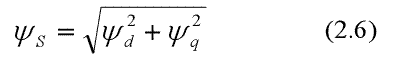
Электромагнитный крутящий момент двигателя выводится из уравнение:

3.1. Источник напряжения инвертора (ИНИ) применяется в ПМСД.
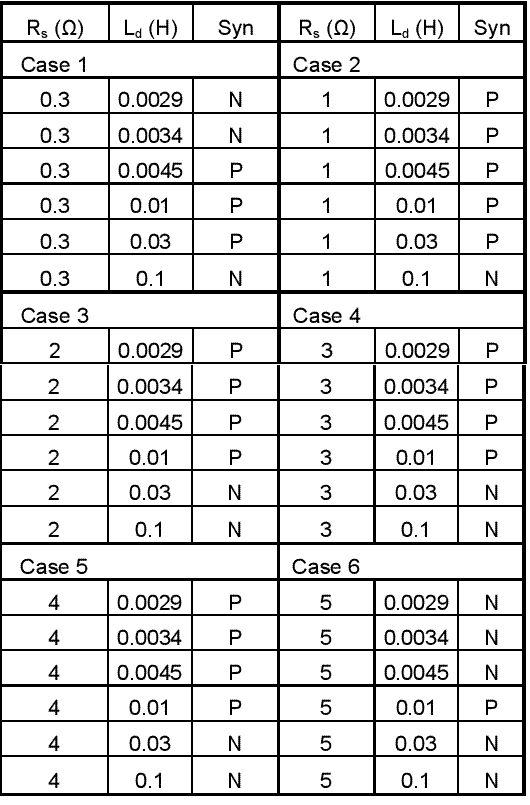
Таблица 1 - Выбор значения Rs и Ld (син - синхронизация, (2,12) N - не возможно, P - возможно)
Когда машина имеет низкое значение сопротивления обмотки статора, то его поведение изменится, даже если это небольшие изменения по продольной оси. (2.13) продольная ось если сопротивление очень мало или очень высоко, синхронная машина не достигнет синхронизма. Чем ближе мы будем получать значения к интервалу, где машина может достигать синхронизма, тем время застоя скорости и крутящий момент больше (рис. 1). Это займет несколько секунд, и это потому мы не можем использовать эту машину на практике. Машина с низким значением сопротивления обмотки статора имеет меньше потерь в обмотке. Если значение сопротивления обмотки статора повышается, машина может достичь синхронизма, даже машина, которая имеет низкую стоимость продольной оси. Когда мы снова поднимаем значение сопротивления Обмотки статора, интервал продольной оси, где Машина может достичь синхронизма, будет уменьшаться. Если значение сопротивления очень высоко и очень маленькое значение индуктивности, машина может не достигать синхронизма.

Рисунок 2 - Rs = 0.3?, Ld = 0,01 H (течения в трех фазах
схемы, крутящий момент и постоянный момент нагрузки ПМСД,
скорость в зависимости от времени ПМСД)
3.2. Источник напряжения инвертора (ИНИ) контролируемый широтно-импульсной модуляцией (ШИМ), примененные к ПСДМ.

Tаблица 2 - Выбор значения R, Ld, Im, T и IL (Im-Момент
инерции ПМСД, T-постоянный крутящий момент, IL-Момент
инерции нагрузки, Н - нет возможности, P - возможно).
При использовании источника питания инвертора (ИНИ), контролируемого широтно-импульсной модуляцией (ШИМ), применяется в ПСДМ значения по продольной оси полного сопротивления и сопротивление обмотки статора, которые не столь большое влияние оказывают на поведение машины. Другой способ, когда мы использовали только ИНИ применительно к ПСДМ значения оказывали большое влияние на поведение машины. В случае 1 мы видим, что ПСДМ может достигать синхронизма при почти всех значениях. Только в измерение, где используется Rs = 20 Ом, машина не может достичь синхронизма, потому что сопротивление статора итак большое. Это сопротивление не хорошо и для практики. Мы можем наблюдать различие между сопротивлениями обмотки статора только в начале процесса. Стабильное значение одно и тоже для всех сопротивлений (без большого сопротивления 20 Ом). В случае 2, когда мы меняем Сопротивление по продольной оси, мы можем наблюдать, что машина имеет такое же поведение, как в случае 1. Так сопротивление по продольной оси оказывает не столь большое влияние на поведение машины, как сопротивление обмотки статора. В случае 3, мы увеличиваем постоянную крутящего момента. Момент инерции ПМСД и шум остается таким же, как и В предыдущих случаях. Этот момент настолько велик, что машина не может достичь синхронизма. Скорость уменьшается. Даже изменения сопротивления обмотки статора не помогло. (Рис. 2)
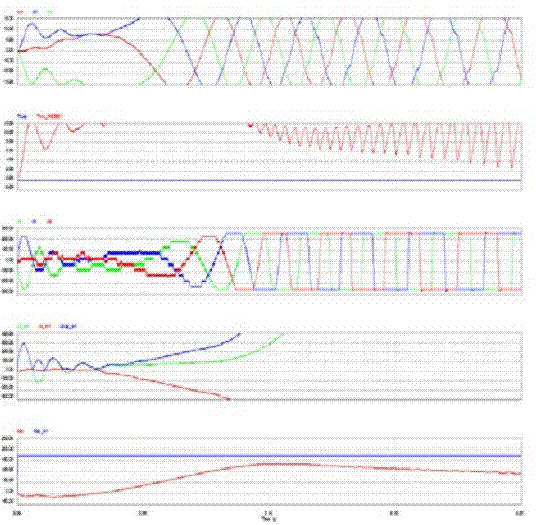
Рисунок 2 - Rs = 2.5?, Ld = 0,03, Im = 1,79, T = 10, IL = 0, син = пр
(Схема замещения потока трех фаз, схема крутящего момента ПМСД
и постоянного крутящего момента нагрузки в зависимости от времени, напряжение
в трех фазах, схема относительно
напряжений Vd, УО и Vmag, моделирования скорости ПМСД и
исходной скорости в зависимости от времени)
В случае 4, мы возвращаем значения постоянного крутящего момента обратно на значение 5, и меняем момент инерции ПМСД. В следующих значениях время застоя больше. Например, на рисунке 3 мы можем наблюдать длительное время застоя, прежде чем машина может достичь синхронизма. Когда мы меняем сопротивление обмотки статора, изменения поведения происходят только в верхней части начала процесса. Если мы используем меньшее сопротивление обмотки статора, мы получим меньшую погрешность. В следующем случае 5, мы сохраняем те же значения, как И в 4, увеличиваем только момент инерции нагрузки. Когда мы используем большие сопротивления обмотки статора 10 Ом, отклонение на вершине очень большое и время застоя тоже большое. Вот почему, машина не может достичь синхронизма. При использовании меньшего сопротивления обмотки статора, время застоя уменьшается и размер отклонения уменьшается.
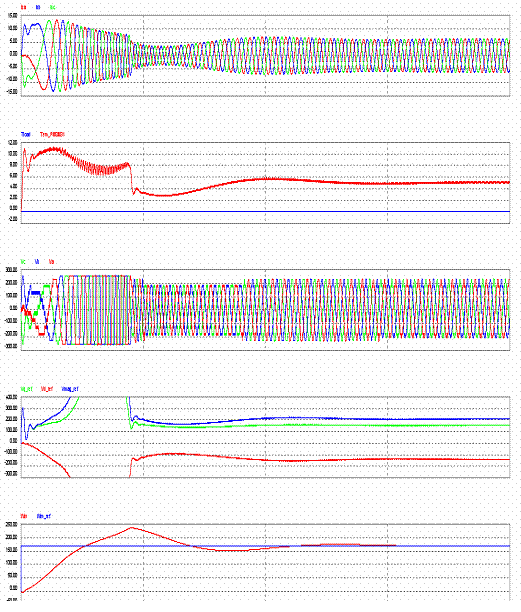
Рисунок 3 - Rs = 10, Ld = 0,03, Im = 2,79, T = 5, IL = 0, син = р
(Схема замещения потока трех фаз, схема крутящего момента ПМСД
и постоянного крутящего момента нагрузки в зависимости от времени, напряжение
в трех фазах, схема относительно
напряжений Vd, УО и Vmag, моделирования скорости ПМСД и
исходной скорости в зависимости от времени).
В тех случаях, 6 и 7, мы уменьшаем момент инерции ПМСД и нагрузки. Машина может достигать синхронизма для всех значений в этих случаях. В случае 8, мы можем наблюдать влияние момента инерции нагрузки на поведение машины. Разница в моменте инерции нагрузки не столь велика, поэтому влияние на поведение машины небольшое. Но если колебание будет большим, отклонение и время застой возрастут.
3.3. Источник напряжения инвертора (ИНИ) с кабельным питанием применительно к ПМСД.
Можно пренебречь индуктивным сопротивлением и сопротивлением поставки кабеля в предыдущих измерениях (ИНИ, ИНИ контролируемый PWM). Мы приняли это предположение, как идеал в этих случаев. Это означает, что сопротивления и индуктивное и реактивное равны нулю. Идеального кабеля не существует в практике. Каждый провод имеет сопротивление. Когда мы используем короткий кабель (10м, R = 0,0469, XL = 0,00099), мы можем наблюдать, что эти небольшие сопротивления системы не влияют на ПМСД. Мы используем кабель длиной 3 км, по последним измерениям. Этот кабель имеет сопротивление 14097 индуктивное и реактивное сопротивление 0,2997 (0,93). Это сопротивление является настолько высоким, что возникает проблема синхронизма (рис. 4). ПМСД может достичь синхронизма только тогда, когда мы используем Значения Rs = 0,3 и Ld = 0,01.

Рисунок 4 - Rs = 1, Ld = 0,01 (ток в трех фазах,
крутящий момент ПМСД и постоянный момент нагрузки,
скорость в зависимости от времени)
3.4. Влияние качества поставляемой электроэнергии и поведении ПМСД.
В этих измерениях мы имеем дело с влиянием качества поставляемой электроэнергии на поведение ПМСД. Показателей качества много. Мы выбираем напряжение асимметрии, напряжения сети и изменения частоты наших измерений. Это задача для ИНИ, которые должны смотреть на качество и на поставку машины. Изменение частоты сети не влияет на поведение ПМСД, потому что инвертор может сделать право частоты на поставку машины. В перенапряжения +10% машина может достигать синхронизма во всех случаях. При пониженном напряжении -10%. ПМСД со значениями Ld = 0.01 и Rs = 5 не могут достичь синхронизма, так как сопротивление обмотки статора большое. Перенапряжения машины лучше, чем пониженное напряжение. При пониженном время, когда машина достигнет синхронизма, больше, чем время от перенапряжения. Если мы использовали импульсный выпрямитель вместо обычных диодов выпрямителей, мы устранили бы эту разницу и двигатель бы достиг синхронизма в случае даже, если все будет выше пониженного напряжения. Мы изменили напряжения в одной фазе, на значение 552V (1%), 500V (10%) и 400 (28%) для создания асимметрии напряжения. В первом измерении (552V), мы находимся в допустимая надбавке, которая приводится в норму асимметрией напряжения. Поведение ПМСД не изменится в этом случае. ИНИ может сделать то же напряжение, как при использовании симметрии напряжения для питания ИНИ. Во втором измерения (500V), мы можем наблюдать разницу на рис. 5. Размер удвоенной амплитуды скорости около 100 об / мин. Эта удвоенная амплитуда не изменится в будущем. И именно поэтому, Машина не может достичь синхронизма.
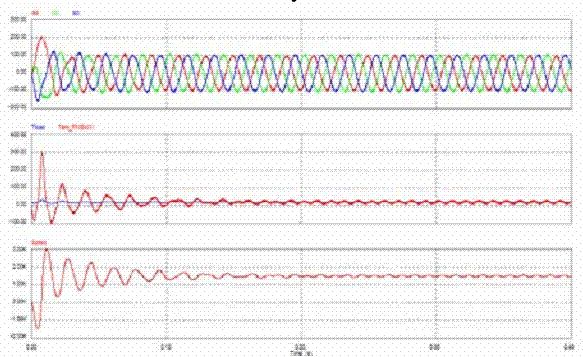
Рисунок 5 - Rs = 1?, Ld = 0,0045 H, Uu = 500V
В следующем измерении, мы меняем напряжение На значение 400V. Графики скорости, крутящего момента и тока аналогичны измерениям предыдущим, только удвоенная амплитуда увеличивается в 300 об / мин. Когда мы увеличиваем сопротивление обмотки статора, изменение поведения ПМСД очень мало. Когда мы увеличить сопротивления по продольной оси, удвоенное увеличение амплитуды и кривая тока сильно деформируется. В эксперименте, когда ИНИ поставляется 2 этап напряжение, кривая тока очень деформирована, то есть мы не можем применить этот ток для ПМСД.
4. Выводы
Заключение ИНИ применительно к ПМСД : Если значение сопротивления обмотки статора повышается, Машина может достичь синхронизма, даже при низко значении сопротивления по продольной оси. Когда мы снова поднимаем значение сопротивления обмотки статора, интервал сопротивления по продольной оси, где машина может достигать синхронизма, будет уменьшаться. Если значение сопротивления очень высоко, и индуктивность очень мала, машина не может достигает синхронизма. Когда мы увеличиваем сопротивление обмотки статора и индуктивность, мы можем заметить, что ИНИ снижается до 50%. Преимущества этого контроля являются его простота и отсутствие PWM. Большая разница, когда мы используем ИНИ при контролируемом PWM применительно к ПМСД, поскольку в этом случае значения сопротивления обмотки статора и сопротивление по продольной оси не столь большое влияние оказывает на поведение ПМСД. Если сопротивление цепи велико получить синхронизм проблематично. ПМСД может достичь синхронизма только тогда, когда мы используем значения Rs = 0,3 и Ld = 0,01. Мы моделировали изменение частоты сети. Это изменение не влияет на поведение ПМСД, потому что инвертор может принимать правильные частоты для питания машины. Если мы используем импульсный выпрямитель вместо обычного диод выпрямителя, мы хотели бы ликвидировать влияние на Изменение напряжения и двигатель достигнет синхронизма во всех случаях даже будет выше, пониженного напряжения. Последней Эксперимент показывает, что две фазы поставляется идентификатор невозможно. Все четыре измерения показывают, что при хорошем дизайне машины, она может достичь синхронизма в Наиболее неблагоприятных оперативных обстановках.
Ссылки.
1. Motores Sinchrones de Imanes Permanents, Manuel
Perez Donsion, Manuel A. Fernandez Ferro, 1990
Universidade de Santiago de Compostela.
2. Elektricke pohony pro dynamicky nfrocne aplikace,
Martin Diblik, 2006 Technicke univerzita v Liberci.
3. Permanent Magnet Synchronous Machine Model for
Real-time SimulationA. B. Dehkordi, A. M. Gole, T. L.
Maguire 2005, International Conference on Power
System Transients in Montreal.
4. Direct Torque Controlof a Permanent Magnet
Synchronous Motor,David Ocen, 2005 Stockholm.