Источник: Всеукраинская научно-техническая конференция студентов «Электротехника, электроника и микропроцессорная техника», 26 – 27 мая 2009 г., ДонНТУ, Донецк.
Успішна робота електричної системи значною мірою залежить від її здатності забезпечити надійне і безперебійне енергопостачання споживачів [1]. Обґрунтування режимів роботи системи, аналіз статичної і динамічної стійкості, дослідження внутрішніх перенапруг, вибір параметрів настройки регулюючих пристроїв і протиаварійної автоматики є актуальною задачею.
Метою цієї роботи є аналіз та дослідження математичних моделей електричної системи і методики дослідження динамічної стійкості.
Для досягнення поставленої мети необхідно вирішити наступні задачі:
- оцінити вплив складності моделі генератора на результати дослідження стійкості;
- обґрунтувати методику оцінки динамічної стійкості режиму електричної системи;
- оцінити адекватність отриманих результатів.
Аналіз великої кількості робіт [2-6] показує, що методи аналізу динамічної стійкості в ЕЕС можуть бути розбиті на такі групи:
- чисельні методи оцінки стійкості у часовій області на основі рішення систем рівняння, які описують перехідні процеси;
- прямі методи по типу Ляпунова;
- експрес-методи;
- методи на основі теорії розпізнання образів.
Чисельні методи оцінки стійкості у часовій області дозволяють: отримати інформацію про зміни параметрів режиму; сформулювати любий сценарій аналізу стійкості.
Однак ці методи не дозволяють:
- визначити область режимів, які необхідно аналізувати (немає рекомендацій для відсічення збурення з точки зору стійкості»);
- безпосередньо оцінити запаси стійкості;
- отримати узагальнюючі рекомендації по керуванню стійкості;
- потребують багатократного вирішення систем керування для оцінки граничних умов стійкості.
Основною перевагою прямих методів оцінки стійкості є безпосереднє обчислення границь динамічної стійкості (без повторних обчислювань), зручне визначення запасів стійкості. Однак застосування цих методів обмежено із-за прийняття істотних припущень при реалізації методів, які основані на теорії Ляпунова. Але прийняття припущень не дозволяють отримати достовірну інформацію про зміну параметрів режиму, а значить реалізувати оптимальне керування конкретним режимом.
Значна кількість робіт була направлена на розробку псевдо – Ляпуновських підходів, які здатні вирішити задачу аналізу динамічної стійкості так, щоб це було достатньо гнучко з точки зору моделювання енергосистем, з точністю, яка не уступає аналізу у часовій області, і ефективно у відношенні обчислювань [5-6].
Ці дослідження дозволили сформулювати такі висновки:
- проблему оцінки області стійкості можна вирішувати, розглядаючи двохмашинний чи одномашинний еквівалент багатомашинної енергосистеми;
- проблему моделювання можна вирішувати шляхом інтеграції прямого методу з урахуванням процесів у часовій області.
На практиці, у ряді випадків аварійні режими ЕС за своїми параметрами (ознаками) подібні до нормально–експлуатаційних. Наприклад, короткі замикання можна вважати подібними до режимів накидання асинхронного навантаження, синхронізації генераторів на паралельну роботу та ін. У цих випадках існуючі методи та засоби оперативного керування режимами ЕС не завжди дозволяють найкращим чином справитися з задачею класифікації аварійних режимів. Для створення автоматизованої системи керування ЕС, необхідно вирішити кілька важливих задач, у тому числі задачу безпомилкового розпізнавання аварійних ситуацій в ЕС.
Оскільки для рішення цієї задачі потрібна обробка значного об’єму статистичних даних, виявлення конкретних специфічних якостей, які належать класу режимів, що розглядається, і прийняття рішення про стан ЕС в умовах невизначеності, то доцільно реалізувати ії методами статистичної теорії розпізнавання образів.
При вирішенні задач розпізнавання, досліджуваний режим, що описується m параметрами (ознаками), представляється у виді вектора (об'єкта) у m-мірному просторі спостережень. Розпізнавання образів – це ухвалення рішення, що установлює приналежність нового, раніше в процесі вивчення об'єкта, що не розглядався, до даного класу об'єктів (образу) шляхом порівняння властивостей цього об'єкта з уже відомими і вивченими. У [2-3] уся сукупність параметрів (ознак),що характеризують аварійну ситуацію в ЕЕС, розбивається на три групи:
- кількісні ознаки, якщо значення ознак можуть бути виражені в чисельному виді (наприклад, параметри режиму, тривалість аварії, опір елементів ЕЕС і т.д.);
- якісні (рангові) ознаки, якщо значення ознаки не виражаються числами, але характеризують різноманітний ступінь прояву якоїсь властивості об'єктів, унаслідок чого можлива ранжировка ознак (наприклад, види коротких замикань, регулятори збудження пропорційної і сильної дії і т.д.);
- класифікаційні (номінальні) ознаки, коли значення ознаки не являються числами і не пов'язані природним упорядкуванням. Цей тип ознаки можна представити при вирішенні задач розпізнавання ситуацій у ЕЕС у виді логічних змінних, що приймають значення нуль або одиниця. До останньої групи ознак відносяться напрямки потоків потужності по лініях, наявність або відсутність АПВ на ПЛ, стан ліній електропередачі і резервних генераторів у ЕЕС (включені або відключені) і т.п.
Для математичного опису процедури розпізнавання використовуються: детерміновані методи; імовірні методи; статистичні методи.
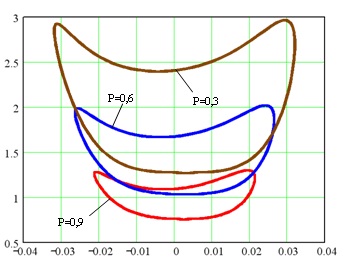
Побудовані поверхні стійкості для генераторів різної потужності (рисунок 1). За результатами графіків можна зробити висновки, що зі збільшенням потужності поверхня стійкості зменшується.

Ці поверхні можуть використовуватися для керування перехідним процесом. Якщо значення границь заздалегідь розрахованої поверхні стійкості зберігати в запам’ятовуючому пристрої, то в перший момент виходу системи на післяаварійну характеристику можна визначити чи збережеться стійка робота станції.
Побудова поверхонь стійкості координатах а1(δ) може бути використана при виборі керуючих впливів.
Таким чином, застосування функціональних залежностей для випередженого визначення стійкості станції в конкретних складних ЕЕС можна встановити на основі попередніх розрахунків перехідних процесів. У цьому випадку побудова областей стійкості для найбільш характерних режимів досліджуваних ЕЕС дозволить суттєво зменшити загальний об’єм необхідних досліджень.
Реалізація випереджальної оцінки стійкості станції в контурі протиаварійного керування системою дозволить проводити вибір керуючих впливів по узагальнюючому показнику, який враховує вплив всіх пристроїв, які впливають на стійкість.
1. Совалов С.А., Семенов В.А. Противоаварийное управление в энергосистемах. - М.: Энергоатомиздат, 1988. - 416 с.
2. Богатырев Л.Л. Распознавание аварийных ситуаций в электроэнергетических системах // Электричество. – 1978. - N6. - С. 9-14.
3. Александров Е.П. Применение теории распознавания образов для классификации режимов сложных электрических систем // Электричество. – 1978. - N9. - С. 76 - 77.
4. Веников В.А., Асамбаев С.Н. Экспресс - оценка устойчивости процесса по его начальной стадии // Изв. АН СССР. Энергетика и транспорт. – 1986. - N3. – С. 22-25.
5. Костерев Н.В. Принцип сведения Ляпунова при анализе периодических движений сложной электрической системы // Проблемы технической электродинамики. – 1978. – Вып. 67. – С. 38-44.
6. Павелла М. Об общей теории Ляпунова к практическому прямому методу анализа динамической устойчивости // Электричество. - 2000. - №6. – С. 14-26.