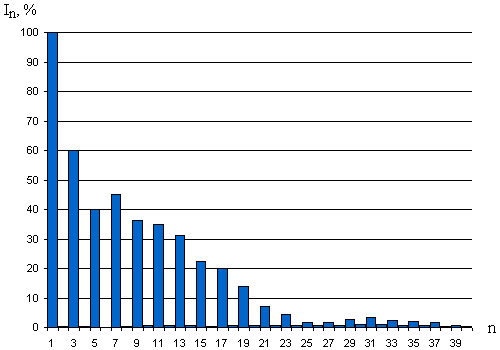
Рисунок 1 – Спектр гармонических составляющих тока КЛЛ Maxus 32w

До 80-х годов XX века в качестве основных электрических потребителей были линейные нагрузки, такие как асинхронные электродвигатели, лампы накаливания, печи сопротивления и т.п. В связи с научно-техническим прогрессом в области электротехники появлялись новые электрические нагрузки, питание которых осуществлялось с использованием разнообразных тиристорных преобразователей и нелинейных элементов. Кривая тока таких нагрузок сильно отличается от синусоидальной формы, что отрицательно сказывается на параметрах питающей электросети, качестве электроэнергии и условиях работы других электроприемников.
В последние годы все больше возрастает применение нелинейных (импульсных) нагрузок, к которым относятся персональные компьютеры, телевизоры, копировальная техника, блоки бесперебойного питания (UPS), газоразрядные лампы, тиристорные регуляторы, кондиционеры, микроволновые печи и многие другие. Из-за нелинейности нагрузок их кривые тока содержат спектр высших гармоник, что приводит к опасным явлениям в сети, которая не рассчитана на это. Высшие гармоники могут приводить к следующим последствиям:
Такая же ситуация наблюдается и в электрических сетях освещения. Происходит постепенная замена старых ламп накаливания (ЛН) на компактные люминесцентные лампы (КЛЛ), потребление электроэнергии которых в среднем в 4 раза ниже, чем у ЛН, а также проектируются новые системы освещения с использованием КЛЛ и люминесцентных ламп (ЛЛ).
В соответствии с планом по переходу на энергосберегающие технологии в Европе с 01 сентября 2009 г. вступил в силу запрет на производство ламп накаливания мощностью от 100 ватт и более, а все их запасы были изъяты с прилавков магазинов. Вся программа перехода на энергосберегающие технологии в самой популярной отрасли освещения рассчитана до 2012 году. 100-ваттные лампы
уже запрещены, в этом году такая же
участь ожидает 75-ваттные лампы,
в 2011
под запрет попадут 60-ваттные, и к сентябрю 2012 года запретят даже самые маломощные − 40- и 25-ваттные. Подобная стратегия энергосбережения поможет экономить в год на электричестве одной среднестатистической семье 50-166 евро. В масштабах Евросоюза это 5-10 миллиардов евро. Закон, запрещающий продажи ламп накаливания с октября 2009 года, приняла Новая Зеландия. Россия также планирует постепенный отказ от ламп накаливания начиная с 2011 года. В США закон о замене традиционных ламп накаливания энергосберегающими
Джордж Буш подписал еще в конце декабря 2007 года. Документ предусматривает, что в течение семи лет потребление энергии лампами накаливания сократится на треть. При этом предполагается, что лампы мощностью 100 ватт выйдут из употребления к 2012 году, 75 ватт − к 2013-му, а 60- и 40-ваттные перестанут освещать американские домовладения к 2014 году [1]. Использование КЛЛ в качесвте замены ЛН имеет большие перспективы на ближайшее будущее и в Украине, учитывая возрастающее с каждым годом внимание к энергосберегающим
технологиям.
Во всех КЛЛ, в отличие от ЛЛ, используются электронные балласты, кривая тока которых отличается от синусоиды намного больше, чем у ЛЛ. В первую очередь это является следствием малых размеров самого балласта КЛЛ, а также снижения стоимости КЛЛ за счет отсутствия элементов, которые приближают кривую тока к синусоидальной форме.
Учитывая все вышеперечисленные факты, становится вопрос о правильном и точном расчете современных сетей электроснабжения, учитывая самые разнообразные нагрузки. Правильный расчет исключит развитие аварийных ситуаций, позволит рассчитывать параметры качества электроэнергии (ПКЭ) и применять меры по предупреждению их возможного снижения.
Так как время-токовые характеристики КЛЛ и ЛЛ отличаются от ЛН и это не учитывается в современных нормативных документах, стоит задача изучить этот вопрос и разработать рекомендации по расчету электрических сетей освещения с использованием этих ламп. Для этого в моей работе используется так называемый «общий» метод расчета электрических сетей. Общность метода заключается в его универсальности: им могут быть рассчитаны все виды нагрузок, так как расчет осуществляется по мгновенным значениям тока и напряжения. Этот метод позволяет точно рассчитывать результирующие параметры сети, находить мгновенные значения необходимых величин, графически представлять конечные результаты расчетов.
Из-за резкопеременного характера потребления тока КЛЛ возникают сложности с нахождением значений интегралов функции тока по времении, особенно, значений их производных. Для устранения этого недостатка в работе применяются сплайн-функции, которые описывают вид кривых тока и напряжения, измеренных дискретно по точкам. Сплайн-функции позволяют с высокой степенью точности находить значения производных в любой момент времени и брать интегралы.
Вследствие того, что КЛЛ находят все большее применение в качестве прямой замены ЛН и являются наиболее нелинейными осветительными нагрузками, дальнейшие исследования и расчеты производились на примере сети освещения с использованием КЛЛ.
В работе было исследовано 14 КЛЛ различной мощности и производителей, были рассчитаны их параметры, проведен анализ и сопоставление характеристик ламп. На примере одной из ламп была рассчитана электрическая сеть освещения.
Путем моделирования сети освещения на примере аудитории 8.411, выполнив замену 18-ти ламп накаливания мощностью 150 Вт на КЛЛ Maxus 32w (по 6 ламп на фазу), были получены кривые тока в проводах четырехфазной сети, кривые падений напряжения в них, а также результирующие кривые фазного и линейного напряжений сети освещения.
1. Составляющие тока и мощности КЛЛ.
Кривая тока КЛЛ, в отличие от ЛН, обладает широким спектром гармонических составляющих. Для лампы Maxus 32w процентные соотношения приведены на рис. 1.
Рисунок 1 – Спектр гармонических составляющих тока КЛЛ Maxus 32w
Вследствие этого, кроме активной и реактивной мощности по проводам протекает дополнительная мощность, называемая мощностью искажений. Она является частью реактивной мощности, которая характеризует процессы, обусловленные взаимодействием разных по частоте гармоник тока и напряжения.
Полная мощность лампы рассчитывается по формуле:

По расчетам параметров КЛЛ Maxus 32w были получены следующие результаты:
P = 27,5 Вт – активная мощность (всех гармоник);
Q = -8,59 вар – реактивная мощность (всех гармоник).
S` = 28,8 ВА – полная мощность без учета мощности искажений;
D = 33,7 вар – мощность искажений;
S = 44,3 ВА – полная мощность КЛЛ.
Из результатов видно, что мощность искажений составляет большую часть действующего значения тока лампы, дополнительно загружая при этом сеть и не выполняя полезной работы. В таблице 1 представлены значения составляющих тока КЛЛ.
Таблица 1 - Значения составляющих тока КЛЛ Maxus 32w
| Maxus 32w | IP, А | IQ, А | IS`, А | ID, А | IS, А |
| 0,12 | -0,037 | 0,126 | 0,147 | 0,193 |
В отличие от КЛЛ, ЛН потребляют из сети только активную мощность (при синусоидальной форме напряжения). Для сравнения приведем расчет приблизительно равной по световому потоку лампы накаливания мощностью 150 Вт (табл. 2).
Таблица 2 - Значения составляющих тока ЛН мощностью 150 Вт
| ЛН 150 Вт | IP, А | IQ, А | IS`, А | ID, А | IS, А |
| 0,652 | 0 | 0 | 0 | 0,652 |
2. Протекание тока в нулевом проводе при равномерном распределении ламп по фазам.
Смоделировав равномерную нагрузку по фазам (по 6 КЛЛ на одну фазу), были получены кривые токов в фазах и в нулевом проводе (рис. 2)

Рисунок 2 – Кривые токов, протекающих в фазах и нулевом проводе
Появление тока в нулевом проводе при равномерно распределенной по фазам нагрузке обусловлено наличием высших гармоник, кратным трем. Так как кривая тока КЛЛ является периодической, значения четных гармоник можно принять равным нулю и в нулевом проводе будет протекать сумма токов нечетных гармоник кратным трем (3-я, 9-я, 15-я и т.д.).
Действующее значение тока в нулевом проводе превышает действующее значение тока в фазном проводе в 1,5 раза (табл. 3). Для сравнения приведем результаты упрощенного расчета этой же сети, но с использованием ламп накаливания при допущении, что кривая напряжения синусоидальна (табл. 4).
Таблица 3 – Значения токов и мощностей при использовании КЛЛ Maxus 32w
| Iд, А | Imax, А | P, Вт | Q, вар | S`, ВА | D, вар | S, ВА | |
| Фаза A | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Фаза B | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Фаза C | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Нулевой провод | 1,74 | 3,81 | 0 | 0 | 0 | 398 | 398 |
Таблица 4 – Значения токов и мощностей при использовании ЛН мощностью 150 Вт
| Iд, А | Imax, А | P, Вт | Q, вар | S`, ВА | D, вар | S, ВА | |
| Фаза A | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Фаза B | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Фаза C | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Нулевой провод | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Согласно ПУЭ (п. 1.3.8) нулевые рабочие проводники должны иметь проводимость не менее 50% проводимости фазных проводников, а в необходимых случаях может быть увеличена до 100%. В нашем случае даже равные сечения фазного и нулевого провода вызовут перегрузку последнего, и это при симметрично расположенной по фазам нагрузке. Значение тока в нулевом проводе будет ещё большим, если лампы будут неравномерно размещены по фазам. Это указывает на то, что действующие на сегодняшний день нормы и правила проектирования для современных электрических сетей неприемлемы.
3. Значительное падение напряжения в реактивной составляющей сопротивления сети.
Падение напряжения складывается из падения напряжения в активном и реактивном сопротивлении сети и для линейной нагрузки рассчитывается по формуле:
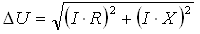
где I – действующее значение тока, А;
R – активное сопротивление провода, Ом;
X – реактивное сопротивление провода при номинальной частоте переменного тока, Ом.
Для нелинейной нагрузки падение напряжения в реактивном сопротивлении зависит от частоты тока, иначе говоря, номера гармоники. Чем выше номер гармоники, тем большим реактивным сопротивлением относительно нее обладает сеть. Реактивное сопротивление n-й гармоники рассчитывается по формуле:

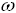 - угловая частота, с-1;
- угловая частота, с-1;
Учитывая гармонический спектр тока КЛЛ (рис. 1) и зависимость величины индуктивного сопротивления провода от номера гармоники тока, был произведен расчет падения напряжения в фазном, нулевом проводе и в петле фаза-ноль. Для всех проводов значения R и X были заданы 0,63 Ом и 0,3 Ом соответственно. На рис. 3 представлены кривые потерь напряжения в фазном, нулевом проводнике и в петле фаза-ноль, на рис. 4 – кривая фазного напряжения с учетом потерь в петли фаза-ноль, а на рис. 5 – кривые фазных и линейного напряжения с учетом потерь напряжения в фазных проводах.
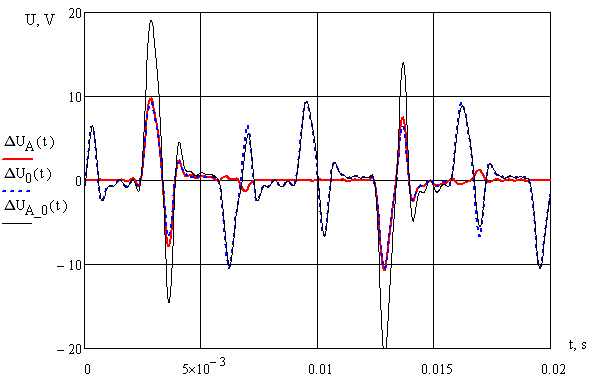
Рисунок 3 – Кривые потерь напряжения в фазном, нулевом проводнике и в петле фаза-ноль
Таблица 5 – Значения потерь напряжения при использовании КЛЛ
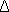 UR, В UR, В |
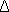 UX, В UX, В |
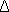 Uд, В Uд, В |
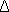 Umax, В Umax, В |
|
| Фаза A | 0,73 | 2,31 | 2,45 | 10,7 |
| Фаза B | 0,73 | 2,31 | 2,45 | 10,7 |
| Фаза C | 0,73 | 2,31 | 2,45 | 10,7 |
| Нулевой провод | 1,09 | 3,76 | 3,91 | 10,43 |
| Фаза-ноль | 1,59 | 5,37 | 5,6 | 21,1 |
Как видно из табл. 5, основная часть падения напряжения (около 90%) происходит именно в индуктивном сопротивлении сети.
Зная кривую падения напряжения в петле фаза-ноль, была получена кривая фазного напряжения сети, питающей осветительную нагрузку, предполагая, что без нагрузки кривая фазного напряжения в сети имеет синусоидальную форму (рис. 4)

Рисунок 4 – Кривая фазного напряжения с учетом потерь в петли фаза-ноль
Также были рассчитаны кривые фазных напряжений с учетом падений напряжения только в фазных проводах (для трехпроводной сети) и рассчитаны линейные напряжения для оценки их показателей качества (рис. 5).
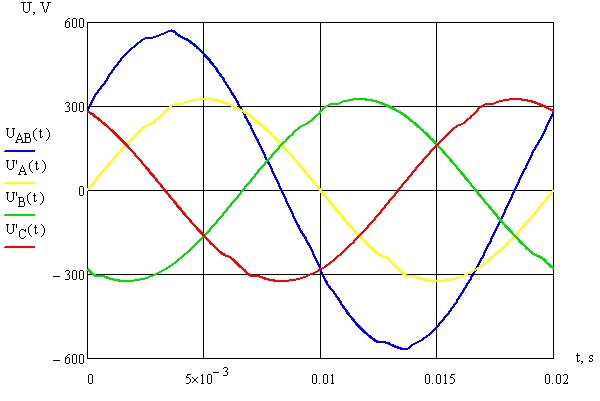
Рисунок 5 – Кривые фазных и линейного напряжений с учетом потерь напряжения в фазных проводах.
Результаты расчетов показывают, что линейные напряжения искажаются в значительно меньшей степени, чем фазные напряжения в четырехпроводной сети, так как отсутствуют потери в нулевом проводе. Для четырехпроводной сети потери в нулевом проводе (при одинаковых сопротивлениях проводов) оказываются выше, чем в фазных за счет того, что в нем протекает сумма высших гармоник кратным трем всех трех фаз.
4. Оптимальное количество измерений кривой тока нелинейных нагрузок.
Учитывая резкопеременный характер потребления тока лампами КЛЛ, и, как следствие, их широкий гармонический спектр, возникает вопрос о необходимом (минимально допустимом) и в то же время оптимальном количестве измерений кривой сигнала в течение его периода. На рис. 5 приведена анимация, которая показывает разницу в изменении во времени кривой тока относительно кривой напряжения при 100 измерениях за период основной гармоники напряжения (частота дискретизации - 5 кГц).

Рисунок 6 – Анимация изменения во времени кривой тока и напряжения.
(51 кадр, 10к/с, 5 циклов, 165 кБ)
Современая техника позволяет осуществлять измерение сигналов с частотой дискретизации, равной гигагерцам, но увеличение количества измерений кроме увеличения точности приводит и к увеличению количества информации, которую необходимо хранить, а главное - обрабатывать. Для нахождения оптимальной частоты дискретизации, при которой можно было бы измерять сигналы с достаточной степенью точности и нахождения по ним всех необходимых согласно ГОСТ параметров качества электроэнергии (ПКЭ), была использована следующая формула:
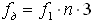
где f1 – частота основной гармоники рассматриваемого сигнала;
n – номер последней гармоники, которая учитывается в расчетах.
Эта формула учитывает то, что минимально необходимое количество измерений синусоиды самой высокой гармоники с частотой равной f1*n должно быть не менее трех за её период. При этом вероятность того, что момент измерения совпадет с моментом перехода синусоиды через ноль и все три значения будут равны нулю, принимается равным нулю.
Беря во внимание то, что ГОСТ 13109-97 при расчете ПКЭ учитывает влияние гармоник до 40-й включительно, подставив в формулу n=40, получим частоту дискретизации
равной 6 кГц (120 измерений за период). При исследовании токовых характеристик КЛЛ была использована частота 5 кГц (100 измерений за период), так как большинство данных по КЛЛ были уже сделаны с этой частотой дискретизации, и повторное измерение с увеличением частоты дискретизации с 5 до 6 кГц повышало точность расчета очень незначительно.
Применив расчет нагрузок по их кривым тока, становятся более очевидными явления, протекающие в электрических сетях с современными нагрузками. Общий метод расчета дает возможность точно рассчитать мгновенные значения всех основных электрических параметров в любой момент времени, наглядно представить результаты расчетов. По результатам расчета кривых суммарных нагрузок можно определить все параметры качества электроэнергии, которые учитывает ГОСТ 13109-97, а также международные
стандарты, так как данный метод предоставляет данные в универсальном для последующей обработки виде.
По результатам расчетов сети с равномерно распределенной по фазам нелинейной нагрузкой минимальное сечение нулевого провода должно быть не менее 150% сечения фазного провода. Становится очевидно, что использование действующих на сегодняшний день правил, нормирующих сечения нулевых рабочих проводников, является неприемлемым.
Резкопеременный характер тока КЛЛ ведет к таким же резким изменениям мгновенных значений сетевого напряжения. При большой мощности нелинейных нагрузок может наблюдаться значительное искажение синусоидальной формы кривой напряжения, что влияет на электромагнитную совместимость других электроприемников, работающех в этой сети и может приводить к преждевременному выходу из строя электрооборудования.
На момент написания автореферата магистерская работа ещё не завершена. Окончательный вариант результатов исследования можно будет взять у меня, либо у моего научного руководителя после декабря 2010 года.
|Об авторе| Библиотека | Ссылки | Отчет о поиске| Индивидуальный раздел |