Рисунок 1 - Спектр гармонійних складових струму КЛЛ Maxus 32w

До 80- х років XX століття в якості основних електричних споживачів були лінійні навантаження, такі як асинхронні електродвигуни, лампи розжарювання, печі опору й т.п. У зв'язку з науково-технічним прогресом у галузі електротехніки з'являлися нові електричні навантаження, живлення яких здійснювалося з використанням різноманітних тиристорних перетворювачів і нелінійних елементів. Крива струму таких навантажень сильно відрізняється від синусоїдальної форми, що негативно позначається на параметрах живильної електромережі, якості електроенергії й умовах роботи інших електроприймачів.
В останні роки усе більше зростає застосування нелінійних (імпульсних) навантажень, до яких відносяться персональні комп'ютери, телевізори, копіювальна техніка, блоки безперебійного живлення (UPS), газорозрядні лампи, тиристорні регулятори, кондиціонери, мікрохвильові печі й багато інших. Через нелінійність навантажень їх криві струму містять спектр вищих гармонік, що приводить до небезпечних явищ у мережі, яка не розрахована на це. Вищі гармоніки можуть приводити до наступних наслідків:
Така ж ситуація спостерігається й в електричних мережах освітлення. Відбувається поступова заміна старих ламп розжарювання (ЛР) на компактні люмінесцентні лампи (КЛЛ), споживання електроенергії яких у середньому в 4 рази нижче, ніж у ЛР, а також проектуються нові системи освітлення з використанням КЛЛ і люмінесцентних ламп (ЛЛ).
У всіх КЛЛ, на відміну від ЛР, використовуються електронні баласти, крива струму яких відрізняється від синусоїди набагато більше, чим у ЛЛ. У першу чергу це є наслідком малих розмірів самого баласту КЛЛ, а також зниження вартості КЛЛ за рахунок відсутності елементів, які наближають криву струму до синусоїдальної форми.
Беручи до уваги всі перераховані вище факти, стає питання про правильний і точний розрахунок сучасних мереж електропостачання, що живлять найрізноманітніші навантаження. Правильний розрахунок виключить розвиток аварійних ситуацій, дозволить розраховувати параметри якості електроенергії (ПКЕ) і застосовувати заходи щодо попередження їх можливого зниження.
У зв’язку з тим, що часо-струмові характеристики КЛЛ і ЛЛ відрізняються від ЛР і це не враховується в сучасних нормативних документах, стоїть завдання вивчити це питання й розробити рекомендації щодо розрахунків електричних мереж освітлення з використанням цих ламп. Для цього в моїй роботі використовується так званий "загальний" метод розрахунків електричних мереж. Особливість методу полягає в його універсальності: їм можуть бути розраховані всі види навантажень, тому що розрахунки здійснюється за миттєвими значенням струму й напруги. Цей метод дозволяє точно розраховувати результуючі параметри мережі, знаходити миттєві значення необхідних величин, графічно представляти результати розрахунків.
Через резкозмінний характер споживання струму КЛЛ виникають складності зі знаходженням значень інтегралів функції струму за часом, особливо, значень їх похідних. Для усунення цього недоліку в роботі застосовуються сплайн-функції, які описують вид кривих струму й напруги, що вимірюються дискретно за точками. Сплайн-функції дозволяють із високим ступенем точності знаходити значення похідних й інтегралів у будь-який момент часу.
Внаслідок того, що КЛЛ знаходять усе більше застосування у якості прямої заміни ЛН і є одним найбільш з найбільш нелінійних освітлювальних навантажень, подальші дослідження й розрахунки проводилися на прикладі мережі освітлення з використанням КЛЛ.
У роботі було досліджено 14 КЛЛ різної потужності й виробників, були розраховані їхні параметри, проведений аналіз і зіставлення характеристик ламп. На прикладі однієї з ламп була розрахована електрична мережа освітлення.
Шляхом моделювання мережі освітлення на прикладі аудиторії 8.411, виконавши заміну 18-ти ламп розжарювання потужністю 150 Вт на КЛЛ Maxus потужністю 32Вт (по 6 ламп на фазу), були отримані криві струмів в проводах чотирьохфазної мережі, криві падінь напруги в них, а також результуючі криві фазної ї лінійної напруг мережі освітлення.
1. Складові струму й потужності КЛЛ.
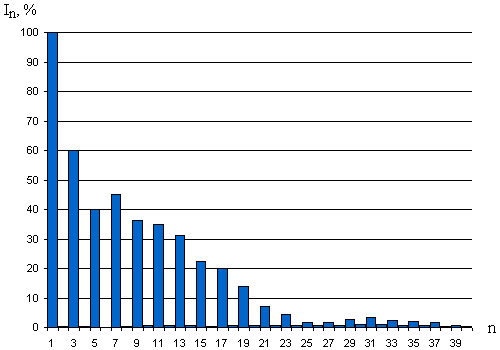
Крива струму КЛЛ, на відміну від ЛН, має широкий спектр гармонійних складових. Для лампи Maxus 32w процентні співвідношення наведені на рис. 1.
Рисунок 1 - Спектр гармонійних складових струму КЛЛ Maxus 32w
Внаслідок цього, крім активної й реактивної потужності по проводах протікає додаткова потужність, що називається потужністю спотворень. Вона є частиною реактивної потужності, яка характеризує процеси, що обумовлені взаємодією різних по частоті гармонік струму й напруги.
Повна потужність лампи розраховується по формулі:

За розрахунками параметрів КЛЛ Maxus 32w були отримані наступні результати:
P = 27,5 Вт - активна потужність (усіх гармонік);
Q = -8,59 вар – реактивна потужність (усіх гармонік);
S` = 28,8 ВА – повна потужність без урахування потужності спотворень;
D = 33,7 вар – потужність спотворень;
S = 44,3 ВА – повна потужність КЛЛ.
З результатів розрахунку видно, що потужність спотворень становить більшу частину повної потужності лампи і додатково завантажує мережу не виконуючи при цьому корисної роботи. У таблиці 1 представлені значення складових струму КЛЛ.
Таблиця 1 - Значення складових токи КЛЛ Maxus 32w
| Maxus 32w | IP, А | IQ, А | IS`, А | ID, А | IS, А |
| 0,12 | -0,037 | 0,126 | 0,147 | 0,193 |
На відміну від КЛЛ, ЛР споживають із мережі тільки активну потужність (при синусоїдальній формі напруги). Для порівняння приведемо розрахунки приблизно рівної за світловим потоком лампи розжарювання потужністю 150 Вт (табл. 2).
Таблиця 2 - Значення складових струму ЛР потужністю 150 Вт
| ЛР 150 Вт | IP, А | IQ, А | IS`, А | ID, А | IS, А |
| 0,652 | 0 | 0 | 0 | 0,652 |
2. Протікання струму в нульовому проводі при рівномірному розподілі ламп по фазах.
Змоделювавши рівномірне навантаження по фазах (по 6 КЛЛ на одну фазу), були отримані криві струмів у фазах і в нульовому проводові (рис. 2).

Рисунок 2 - Криві струмів, що протікають у фазах і нульовому проводові
Поява струму в нульовому проводові при рівномірно розподіленому по фазах навантаженню обумовлена наявністю струмів вищих гармонік, кратним трьом. Тому що крива струму КЛЛ є періодичної, значення парних гармонік можна прийняти рівним нулю й у нульовому проводі буде протікати сума струмів непарних гармонік кратним трьом ( 3-я, 9- я, 15- я і т.д.).
Діюче значення струму в нульовому проводові перевищує діюче значення струму у фазному проводові в 1,5 рази (табл. 3). Для порівняння приведемо результати спрощеного розрахунків цієї ж мережі, але з використанням ламп розжарювання при допущенні, що крива напруги синусоїдальна (табл. 4).
Таблиця 3 - Значення струмів і потужностей при використанні КЛЛ Maxus 32w
| Iд, А | Imax, А | P, Вт | Q, вар | S`, ВА | D, вар | S, ВА | |
| Фаза A | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Фаза B | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Фаза C | 1,16 | 4,37 | 165 | -51,6 | 173 | 202 | 266 |
| Нульовий провід | 1,74 | 3,81 | 0 | 0 | 0 | 398 | 398 |
Таблиця 4 – Значення струмів і потужностей при використанні ЛР потужністю 150 Вт
| Iд, А | Imax, А | P, Вт | Q, вар | S`, ВА | D, вар | S, ВА | |
| Фаза A | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Фаза B | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Фаза C | 3,9 | 5,53 | 900 | 0 | 900 | 0 | 900 |
| Нульовий провід | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Згідно з ПУЕ (п. 1.3.8) нульові робочі провідники повинні мати провідність не менш 50% провідності фазних провідників, а в необхідних випадках вона може бути збільшена до 100%. У нашому випадку навіть рівні перетини фазного й нульового проводу спричинять перевантаження останнього, і це при симетрично розташованому по фазах навантаженню. Значення струму в нульовому проводі буде ще більшим, якщо лампи будуть нерівномірно розміщені по фазах. Це вказує на те, що діючі на сьогоднішній день норми й правила проектування для сучасних електричних мереж є неприйнятними.
3. Значне падіння напруги в реактивній складовій опору мережі.
Падіння напруги складається з падіння напруги в активному і реактивному опорі мережі і для лінійного навантаження розраховується по формулі:
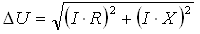
где I – діюче значення струму, А;
R – активний опір проводу, Ом;
X – реактивний опір проводу при номінальній частоті змінного струму, Ом.
Для нелінійного навантаження падіння напруги в реактивному опорі залежить від частоти струму, інакше кажучи, чим вище номер гармоніки струму, тим більший реактивний опір відносно неї має мережа. Реактивний опір n-ї гармоніки розраховується по формулі:

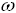 - кутова частота, с-1;
- кутова частота, с-1;
Враховуючи гармонійний спектр струму КЛЛ (мал. 1) і залежність величини індуктивного опору дроту від номера гармоніки струму, було зроблено розрахунок падіння напруги у фазному, нульовому проводі і в петлі фаза-нуль. Для всіх проводів значення R і X були задані 0,63 Ом і 0,3 Ом відповідно. На мал. 3 представлені криві втрат напруги у фазному, нульовому провіднику і в петлі фаза-нуль, на мал. 4 – крива фазної напруги з врахуванням втрат в петлі фаза-нуль, а на мал. 5 – криві фазних і лінійної напруги з врахуванням втрат напруги у фазних проводах.
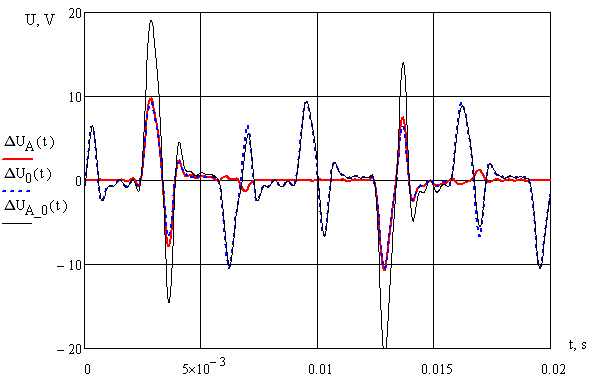
Рисунок 3 – Криві втрат напруги у фазному, нульовому провіднику і в петлі фаза-нуль
Таблиця 5 – Значення втрат напруги при використанні КЛЛ
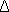 UR, В UR, В |
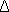 UX, В UX, В |
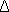 Uд, В Uд, В |
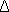 Umax, В Umax, В |
|
| Фаза A | 0,73 | 2,31 | 2,45 | 10,7 |
| Фаза B | 0,73 | 2,31 | 2,45 | 10,7 |
| Фаза C | 0,73 | 2,31 | 2,45 | 10,7 |
| Нульовий провід | 1,09 | 3,76 | 3,91 | 10,43 |
| Фаза-нуль | 1,59 | 5,37 | 5,6 | 21,1 |
Як видно з таблиці. 5, основна частина падіння напруги (близько 90%) відбувається саме в індуктивному опорі мережі.
Знаючи криву падіння напруги в петлі фаза-нуль, була отримана крива фазної напруги мережі, що живить освітлювальне навантаження, маючи на увазі, що без навантаження крива фазної напруги в мережі має синусоїдальну форму (рис. 4)

Рисунок 4 – Крива фазної напруги з врахуванням втрат у петлі фаза-нуль
Також були розраховані криві фазної напруги з урахуванням падінь напруги лише у фазних проводах (для трьохпровідної мережі) і розрахована лінійна напруга для оцінки їх показників якості(рис. 5).
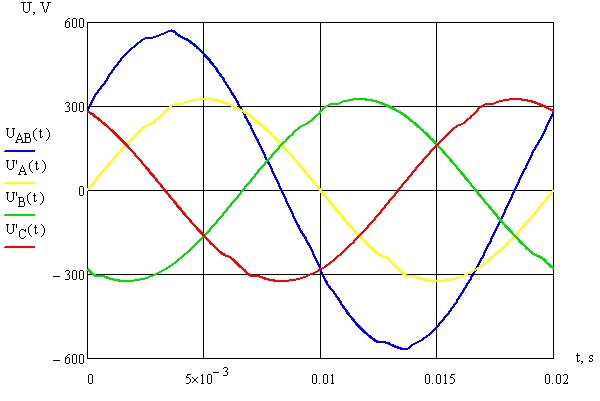
Рисунок 5 – Криві фазних і лінійної напруг, враховуючи втрати напруги у фазних проводах.
За результатами розрахунків видно, що лінійна напруга в чотирьохпровідній мережі спотворюється в меншій мірі, ніж фазна напруга, оскільки відсутні втрати в нульовому проводі. Для чотирьохпровідної мережі втрати в нульовому проводі (при однакових опорах проводів) є більшими, ніж у фазних за рахунок того, що у ньому протікає сума струмів вищих гармонік кратним трьом від усіх трьох фаз.
Застосувавши розрахунки навантажень за їх кривими струму, стають більш очевидними явища, що відбуваються в електричних мережах із сучасним навантаженням. Загальний метод розрахунків дає можливість точно розрахувати миттєві значення всіх основних електричних параметрів у будь-який момент часу, наочно представити результати розрахунків. За результатами розрахунків кривих сумарного навантаження можна визначити всі параметри якості електроенергії, які враховує ДЕРЖСТАНДАРТ 13109-97, а також
інші міжнародні стандарти, тому що даний метод надає дані в універсальному для наступної обробки виді.
За результатами розрахунків мережі з рівномірно розподіленої по фазах нелінійним навантаженням мінімальний переріз нульового проведення повинне бути не менш 150% перерізу фазного проводу. Стає очевидно, що використання діючих на сьогоднішній день правил, що нормують переріз нульових робочих провідників, є неприйнятним.
Різкозмінний характер струму КЛЛ веде до таких же різких змін миттєвих значень напруги мережі. При великій потужності нелінійних навантажень може спостерігатися значне викривлення синусоїдальної форми кривої напруги, що впливає на електромагнітну сумісність інших электроприймачів, що підключені до цієї мережі й може призводити до передчасного виходу з ладу електроустаткування.
На час написання автореферату магістерська робота ще не закінчена. Остаточний варіант результатів дослідження можна буде взяти у мене, або у мого наукового керівника після грудня 2010 року.