Вентильный двигатель – электромеханическая система, которая состоит из синхронной машины и преобразователя частоты (ПЧ),
в которой фазы ПЧ переключаются в функции положения ротора. Вследствие отсутствия механического коллектора синхронный
двигатель с постоянными магнитами (СДПМ) имеет значительные преимущества перед двигателем постоянного тока:
• отсутствие узлов, которые требуют техобслуживания – безколлекторная машина;
• обеспечение взрывобезопасности;
• большая перегрузочная способность по моменту;
• высокое быстродействие, возможность оптимизации режимов работы по скорости и нагрузке;
• наивысшие энергетические показатели;
• высокая надёжность и повышенный ресурс работы;
• низкий перегрев электродвигателя при работе в режимах с возможными перегрузками.
Таким образом, преимущества СДПМ с электронными системами управления объединяют в себе лучшие свойства
бесконтактных двигателей и двигателей постоянного тока, а часто и превосходят их. В связи с этими преимуществами
СДПМ всё чаще вытесняют двигатели постоянного тока из традиционных им сфер использования. Сейчас на основе СДПМ
строятся следящие электропривода подачи верстатов с численным программным управлением и промышленными роботами,
электропривода бытовых приборов (магнитофоны, вентиляторы компьютерных блоков питания, дисководы и др.)
низкой и очень низкой мощности [7].
Актуальность темы
СДПМ с синусоидальным управлением током используют для построения систем векторного управления моментом
и скоростью, которое позволяет обеспечивать высокое качество характеристик ЭП как в статике, так и в динамике, так как при этом
формируется раздельное управление электромагнитными и механическими величинами. В настоящее время традиционно используют
такие актуальные направления усовершенствования промышленных электроприводов:
• усовершенствование силовой схемы и алгоритмов управления коммутацией современных полупроводниковых преобразователей энергии,
которые наиболее часто выполняются на основе скалярной или векторной широтно–импульсной модуляции (ШИМ);
• усовершенствование алгоритмов управления за счёт введения в число регулируемых координат, которые не могут быть измерены
непосредственно (магнитное потокосцепление, электромагнитный момент);
• отход от применения механических датчиков на валу двигателя (для измерения скорости, углового положения), что
позволяет повысить эксплуатационную надёжность ЭП.
Цели и задачи работы
Цель работы – исследование системы векторного управления электроприводом на основе синхронной машины с постоянными
магнитами в зависимости от настроек, которые применяются при наладке контуров регулирования.
Объектом исследования является система векторного управления электроприводом на основе синхронной машины с постоянными
магнитами с идентификатором параметров.
Главные задачи исследования – идентификация потокосцепления статора, вычисление электромагнитного момента, идентификация
скорости, определение начального углового положения ротора.
Основное содержание работы
1 Математическое описание и структурная схема СДПМ во вращающейся системе координат, ориентированной по ротору
При исследовании режимов работы во вращающихся электрических машинах целесообразно использовать координатную систему, жёстко связанную с ротором [6]. Поскольку ротор исследуемой машины имеет магнитную асимметрию, то есть разные магнитные проводимости в двух взаимно перпендикулярных осях, пространственные векторы будут раскладываться на две составляющие в направлении продольной (d) и поперечной (q) осях, причём направление оси d принимается за действительную ось, а q – за мнимую.
Уравнение, описывающее электрическую часть синхронной машины с постоянными магнитами в координатной системе, вращающейся со скоростью ротора, с учётом отсутствия роторных обмоток может быть получено на основе 2-го закона Кирхгофа:
(1)
где 
– результирующий вектор напряжения на обмотке статора;
– вектор потока ротора;
– ЕДС от потока рассеивания статора;
– противо–ЕДС, обусловленная основным магнитным потоком машины, что образуется магнитами ротора.
Рисунок 1 – Векторная диаграмма СДПМ (GIF-анимация из 7 кадров, число повторений 5, размер анимации 31,5 КБ)
Раскладывая в выражении (1) векторы на действительные и мнимые части по осях d, q, получаем систему уравнений:
(2)
Вращающий момент двигателя, с учётом на совпадение направления вектора с осью магнитного поля ротора d, можно записать таким способом:
(3)
Условие механического равновесия описывается выражением:
(4)
Объединяя выражения (2), (3), (4), получаем систему уравнений, которая описывает работу синхронной машины. Упростим запись уравнения, используя оператор Лапласа, заменив
После преобразований получаем:
(5)
где 
– постоянная времени двигателя.
На основании уравнений (5) строим структурную схему синхронного двигателя с возбуждением от постоянных магнитов, которая изображена на рис.2 [10].
Рисунок 2 – Структурная схема СДПМ
2 Идентификация регулируемых координат системы
В настоящее время актуальной есть задача идентификации регулируемых координат: потокосцепления статора, скорости,
момента, начального углового положения ротора. Идентификатор координат обеспечивает достаточную точность. Восстановленные
сигналы могут быть использованы для организации регулирования, а также для усовершенствования алгоритма управления.
Современные подходы к решению задачи идентификации не предусматривают наличия на валу двигателя механических датчиков, что
позволяет повысить эксплуатационную надёжность электроприводов, в том числе при их эксплуатации в агрессивных и взрывоопасных средах.
На данном этапе исследований разработано только идентификатор потокосцепления, момента и скорости.
Делаются шаги для дальнейшего определения начального углового положения ротора.
2.1 Идентификация потокосцепления статора
Задача идентификации потокосцепления статора – определить в каждый момент времени мгновенное значение вектора потокосцепления
статора и углового положения, не прибегая при этом к непосредственному измерению магнитного потока.
На рис.3 представлена замкнутая схема наблюдателя потока статора, которая представляет собой комбинацию модели тока и напряжения.
При высоких скоростях лучше модель напряжения, так как влияние сопротивления статора небольшое в то время, как при малых скоростях
лучше модель тока, так как она работает с нулевой частоты (скорости). ПИ – корректор предназначен для этого разграничивания.
Рисунок 3 – Наблюдатель потока статора
Уравнение напряжения в координатах статора:
Уравнения потокосцепления и тока статора в координатах d, q:
Ортогональные проекции вектора потокосцепления статора поступают
в векторный анализатор (ВА), который вычисляет модуль вектора потокосцепления статора:
(6)
и гармонические функции его углового положения:
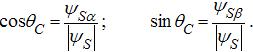
2.2 Идентификация электромагнитного момента
При известных значениях проекций
момент СДПМ может быть вычислен по формуле:
Структурная схема соответствующего идентификатора момента СДПМ приведена на рис.4.
Рисунок 4 – Структурная схема идентификатора момента
2.3 Идентификация скорости
Современные принципы идентификации скорости двигателей переменного тока используют математическое описание двигателя в неподвижной ортогональной системе координат
. При этом идентификаторам присущи недостатки,
которые заключаются в необходимости реализации операций интегрирования, что приводит к накоплению ошибки особенно при низких частотах вращения двигателя.
Математическое описание электромагнитных процессов в электроприводе на
основе синхронного двигателя с возбуждением от постоянных магнитов имеет вид [2]:
(7)
где 
– проекции векторов напряжения,
тока и потокосцепления статора на оси стационарной системы координат статора
соответственно.
Анализ (7) отображает возможность определения проекций
двумя способами – во–первых, используя
информацию о измеренном напряжении и токе статора и применении операции интегрирования; во–вторых, используя информацию о номинальном значении
потокосцепления постоянных магнитов и измеренный ток статора.
При известных значениях проекций
и их производных скорость СДПМ может быть вычислена по формуле:
что вместе с выполненым анализом (7) позволяет допустить, что при построении алгоритма идентификации скорости можно уйти от операции интегрирования.
Структурная схема соответствующего идентификатора скорости СДПМ приведена на рис.5.
Рисунок 5 – Структурная схема идентификатора скорости СДПМ
Проведенные исследования методом математического моделирования показали, что идентификатор координат обеспечивает достаточную точность. Восстановленные сигналы могут быть
использованы для организации регулирования при отказе от применения механических датчиков на валу СДПМ, а также для усовершенствования алгоритма управления.
Рисунок 6 – Идентификация координат электропривода при работе системы векторного управления СДПМ
Заключение
Сейчас ведётся разработка системы векторного управления
СДПМ. Обобщённая функциональная схема системы векторного управления моментом, скоростью и угловым положением ротора СДПМ представлена на рис.7.
Реализация векторного управления предусматривает реализацию свойств
частотно–токового управления. То есть, чем точнее и быстродействующее будет подсистема векторного регулирования током ПВРТ, тем более качественную систему можно построить.
В настоящее время таких способов два: ПИ-регулирование тока во вращающейся системе координат, релейное управление током в фазных координатах [6].
Рисунок 7 – Функциональная схема системы векторного управления СДПМ
При написании данного автореферата магистерская работа не завершена.
Окончательный вариант работы можно получить у автора или научного руководителя после декабря 2010.
Обзор литературы
1. Майборода В. Н. Исследование сервоприводов на основе синхронных машин с постоянными магнитами (
http://masters.donntu.ru/2008/eltf/mayboroda/diss/index.htm)
2. Ищенко И. В. Исследование систем управления электроприводами на основе вентильных двигателей
(http://www.masters.donntu.ru/2009/eltf/ishchenko/diss/index.htm )
3. Божко В.В., Толочко О.І., Чекавський Г.С. «Аналіз впливу перехресних зв'язків в
системі векторного керування СДПМ»
4. Сарычев А.П., Портной Ю.Т., Раскин Л.Я. и др. «Векторное бездатчиковое
управление электроприводом на базе СДПМ»
5. Корельский Д.В. «Обзор современных методов управления СДПМ»//Радіоелектроніка. Інформатика. Управління. - 2001. №2 - с.155-159
6. Соколовский Г. Г. Электроприводы переменного тока с частотным регулированием. – 265 с.
7. Казачковський М. М. Комплектні електроприводи. – Дніпропетровськ, Обліково-видавн. 2003. – 224 с.
8. Герман-Галкин С. Г. Компьютерное моделирование полупроводниковых систем в MATLAB 6.0. – СПб.: КОРОНА принт, 2001. – 320 с.
9. Овчинников И. Е. Вентильные электрические двигатели и привод на их основе (малая и средняя мощность): Курс лекций. СПб.: КОРОНА-Век, 2006. – 336 с.: ил.
10. Виноградов А.Б. Векторное управление электроприводами переменного тока/ГОУВПО «Ивановский государственный энергетический университет имени В.И. Ленина». - Иваново, 2008. - 298с.
ДонНТУ >
Портал магистров ДонНТУ ||
Об авторе | Библиотека | Ссылки |
Отчёт о поиске || Моё увлечение вязанием
