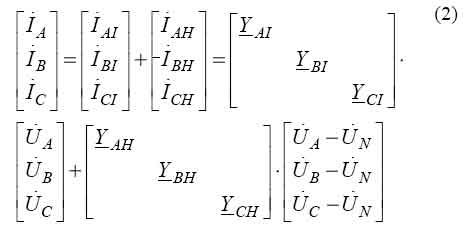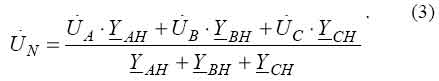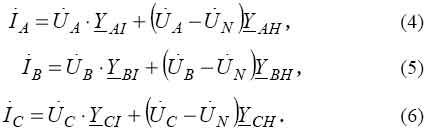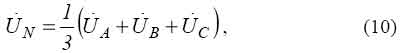Definition of complex admittance of electric isolation without disconnection of electrical equipment

Nikolay Grebchenko1, Igor Koval 2, Aleksey Sidorenko1, Mariya Smirnova1 1Donetsk National Technical University (Donetsk, Ukraine), 2PLC "PES-Energougol"(Donetsk, Ukraine)
gvn@donntu.ru, offise@pes.dn.ua, sid@mirtes.donbass.com, mary_sm@mail.ru

Abstract-The method of uninterrupted measuring of complex admittance of the electric equipment isolation is proposed.

   In order to control periodically the isolation quality various ways of measuring isolation active admittance by means of meggers or indirect methods are widely applied. These ways are based on measuring the current flowing through isolation when applied voltage is constant. Reactive admittance is not defined in this case.

Various methods of control tests of isolation may also be related to the periodic control of isolation [1]:

• tests by high voltage application allowing to check a level of short-term breakdown strength of isolation;
• measurements of partial discharges intensity and value of tg ? and tests by the increased voltage, allowing to estimate long breakdown strength of isolation;
• the preventive tests allowing to estimate a condition of isolation and its suitability to long operation.

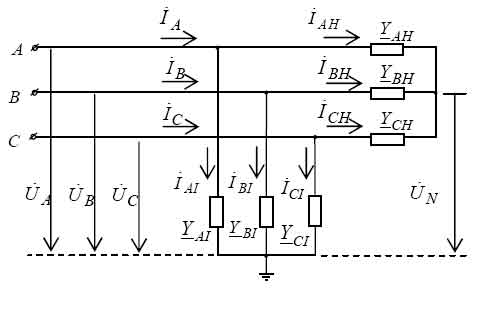
   However, efficiency of the periodic control of isolation essentially decreases at increase of time interval between tests, and reduction of these time intervals is limited by possibilities to shut down the equipment and by growth of labour costs to carry out the tests. Only the continuous control of isolation parameters can provide the timely detection of isolation damages. Lately years the big attention has been given to working out the methods and equipments for automatic continuous control of isolation at operating voltage on the basis of measuring dielectric characteristics and registration of partial discharges [1]. Methods of measuring an isolation resistance and absorption factor are most widely applied to control the condition of isolation of electric machines in operation. The isolation condition is most fully characterized by its complex admittance [2]. The known methods of definition of isolation complex admittance have disadvantages, which do not allow to apply them for the continuous control. Besides, they are not suitable for such feeders as a cable-engine and a cable-transformer.
   For example, the ways of definition of network phase isolation parameters relatively the ground [3] are based on creation of temporary asymmetry which is created artificially by connection a capacity between one of the phases and the ground. To realize this it is necessary to switch-off the feeder for the period of taking the measurements. For the networks with compensation of capacity currents there are the methods expounded in [4].

   Changing of isolation complex admittance of a feeder leads to changing the parameters of its mode. Therefore to define the parameters of isolation it is necessary to solve the task of synthesis of the electric circuit parameters, when the scheme and the values of currents and voltages characterizing the mode of this circuit operation are known [5]. The isolation is represented by the corresponding shunt admittance in an equivalent circuit of electric equipment. Then the analysis of the received values of the scheme parameters is made. The decision whether it is possible to use the feeder further is made on the basis of comparison with admissible values of the shunt admittances of the feeder phases.

   Elements of electric systems can be represented by an equivalent circuit, which is shown in Fig.1. Most simply it is carried out for loading feeders. Electric motors feeders are of the utmost interest.

Fig. 1. The equivalent circuit of a loading feeder in a network with the insulated neutral

   According to the equivalent circuit of connection (Fig.1) the correlation for vectors of phase currents of a feeder IA , IB and IC in a normal mode of operation in the matrix form is as follows [5]:

   Or

where I A, I B, I C - the vectors of phase currents of loading of a feeder; IAI , IBI , ICI - the vectors of currents flowing through insulation of phases of a feeder; Y AI , Y BI , Y CI - shunt complex admittances of phases isolation in relation to the ground (diagonal matrix Y I D ); A U, B U, C U- the vectors of phases voltages in relation to the ground; Y AH , Y BH , Y CH - longitudinal phase complex admittances of loading of a feeder (diagonal matrix YHD );
U - voltage of a neutral of connection in relation to the ground, which can be found by the method of two potentials,

   Longitudinal and shunt complex admittances of a cable or an air-line feeder are taken into account in corresponding admittances of loading of the feeder.
   From the correlation (2) the vectors of feeder phase currents are the following:

   As it seen from the received simultaneous equations (4) - (6) complex admittances of phases isolation can be defined without disconnecting equipment. For this purpose it is necessary to define vectors of phase currents I A, I B and I C, vectors of phase voltages in relation to ground U A, U B, U C and a vector of voltage of the feeder neutral in relation to ground U N. However, in the equations (4) - (6) both shunt complex admittances of phases isolation in relation to ground Y AI , Y BI , Y CI and longitudinal phase complex admittances of loading of a feeder Y AH , Y BH, Y CH are unknown. Thus, six unknowns are in three equations, therefore the simultaneous equations like this cannot be solved. Solution of this system can be found if the parameters of load phases are known or when the symmetry of loading is assumed.
   If longitudinal phase complex admittances of loading of connection Y AH , Y BH , Y CH are known, parameters of phases isolation are defined from (4) - (6) as follows:

   In phase admittances of loading are equal Y AH = Y BH = Y CH the definition of admittances of isolation becomes a little simpler since measuring neutral-point displacement voltage N U becomes unnecessary. It follows from the fact that expression (3) takes the following form:

i.e. neutral-point displacement voltage N U is rated using known phase voltages in relation to the ground. However it is necessary to bear in mind that in expression (10) the vectors of voltages A U , B U, C U depend not only on value of complex admittances of phase isolation of a feeder Y AI , Y BI , Y CI , but they also depend on a mode and parameters of elements of all electrically connected network.