Алексей Шалин, д.т.н., профессор кафедры электрических станций. Новосибирский государственный технический университет
Андрей Хабаров, инженер
Источник: электронный журнал "Всё о релейной защите" 2009.
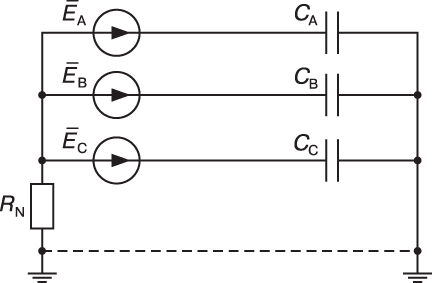
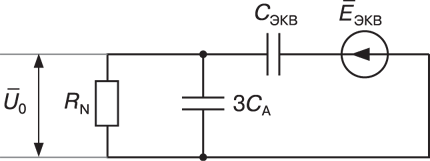
Напряжение нулевой последовательности
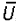 0 (напряжение на резисторе RN)
определяется через параметры остальных элементов схемы в соответствии
со следующим выражением:
0 (напряжение на резисторе RN)
определяется через параметры остальных элементов схемы в соответствии
со следующим выражением: (1)
(1) 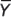 i = jwCi – проводимости фаз
сети (для емкостей);
i = jwCi – проводимости фаз
сети (для емкостей);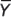 N = 1/RN– проводимость нейтрали
(при наличии заземляющего резистора).
N = 1/RN– проводимость нейтрали
(при наличии заземляющего резистора).Подставив соответствующие величины проводимостей в (1), после несложных преобразований получим:
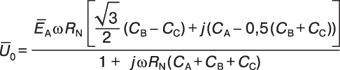 (2)
(2) (3)
(3)
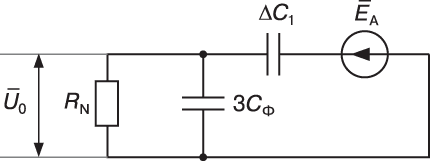
Для этой схемы легко получить расчетное выражение (3), что подтверждает правильность предложенного способа составления расчетной схемы нулевой последовательности.
Рассмотрим теперь случай уменьшения емкости фазы А, что
соответствует 0 ![]() k <
1. При этом СВ = СС = СФ, СА = kСФ. На рис. 3 показана расчетная схема
нулевой последовательности, которая была получена для рассматриваемого
случая. Здесь ЭДС фазы А уменьшена вдвое и направлена в противоположную
сторону по сравнению с предыдущей схемой, а последовательно с ней
включена удвоенная емкость DС2 = СФ(1 – k), на которую
уменьшилась по сравнению с симметричным режимом емкость фазы А. Емкость
линии представлена утроенной емкостью фазы А 3kСФ, то есть минимальной
из трех фазных емкостей.
k <
1. При этом СВ = СС = СФ, СА = kСФ. На рис. 3 показана расчетная схема
нулевой последовательности, которая была получена для рассматриваемого
случая. Здесь ЭДС фазы А уменьшена вдвое и направлена в противоположную
сторону по сравнению с предыдущей схемой, а последовательно с ней
включена удвоенная емкость DС2 = СФ(1 – k), на которую
уменьшилась по сравнению с симметричным режимом емкость фазы А. Емкость
линии представлена утроенной емкостью фазы А 3kСФ, то есть минимальной
из трех фазных емкостей.
Для этой схемы также легко получить расчетное выражение (3), что
свидетельствует о правильности способа составления расчетной схемы
нулевой последовательности.

НЕРАВЕНСТВО ФАЗНЫХ ЕМКОСТЕЙ
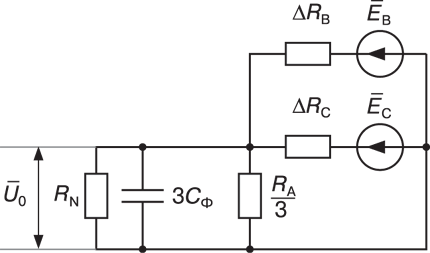
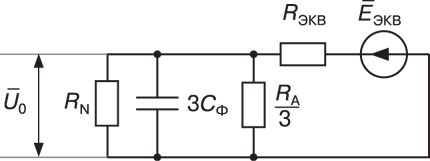
Расчетная схема нулевой последовательности для рассматриваемого случая приведена на рис. 4. Здесь, DCВ = СВ – СА, DCС = СС – СА.
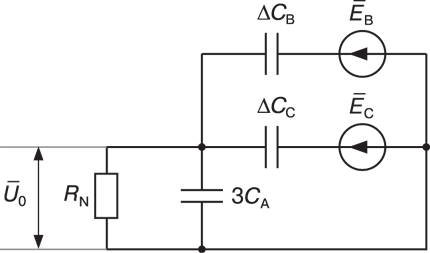
 ЭКВ определится следующим образом:
ЭКВ определится следующим образом: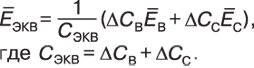
Расчетная схема нулевой последовательности для рассматриваемого случая приведена на рис. 6. Здесь
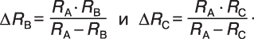

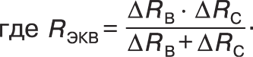
Неравенство индуктивностей между фазами и землей
Рассмотрим способ построения
расчетной схемы нулевой по-следовательности для общего случая
неравенства индуктивностей между фазами и землей, когда индуктивности в
каждой из фаз различны и равны соответственно LA, LB и LC, причем LA
> LB > LC.В этом случае в качестве симметричной схемы
принимаем такую, в которой все индуктивности в фазах равны максимальной
из реальных величин, то есть LA.
Расчетная схема нулевой последовательности для рассматриваемого случая
приведена на рис. 8. Здесь

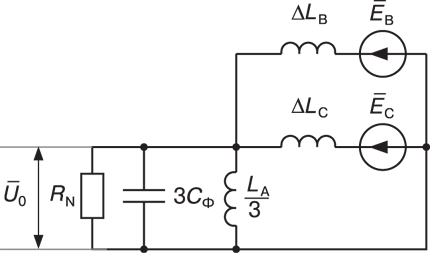
 ЭКВ определится следующим образом:
ЭКВ определится следующим образом: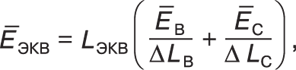

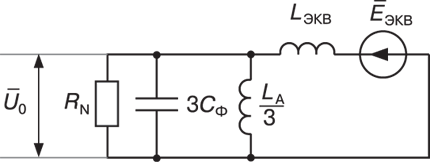
НАЛИЧИЕ ОДИНАКОВЫХ НЕСИММЕТРИЙ В ДВУХ ЛИНИЯХ
В схеме реальной сети может
присутствовать сразу несколько несимметрий. Для расчета напряжений и
токов небаланса в защите от ОЗЗ, появляющихся в рассматриваемом случае,
следует составить полную расчетную схему замещения нулевой
последовательности с учетом приведенных выше рекомендаций.
На рис. 10 приводится пример составления расчетной схемы замещения
нулевой последовательности для сети, питающейся от одной секции
подстанции (см. «Новости ЭлектроТехники» № 4(40)
2006, стр. 49, рис. 1), при появлении несимметрии в двух линиях. Здесь
в качестве примера рассматривается случай, когда емкость в фазе А линии
Л1 увеличилась на DC, а в той же фазе линии Л2 – уменьшилась
на ту же величину. При этом величины эквивалентных ЭДС линий Л1 и Л2 в
расчетной схеме по рис. 10 составят соответственно  A и –
A и – A/2, а величины эквивалентных емкостей
– DC и 2DC. Легко убедиться, что в рассматриваемом случае
A/2, а величины эквивалентных емкостей
– DC и 2DC. Легко убедиться, что в рассматриваемом случае 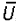 0 = 0, поскольку сеть в целом осталась
симметричной. Но ток нулевой последовательности по линиям Л1 и Л2
протекает и равен:
0 = 0, поскольку сеть в целом осталась
симметричной. Но ток нулевой последовательности по линиям Л1 и Л2
протекает и равен: 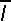 0Л1 = –
0Л1 = – 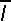 0Л2 =
0Л2 =  A· jwDC.
A· jwDC.
Хотя этот ток и не может привести к срабатыванию направленной защиты,
поскольку 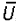 0 = 0, но отличить его при замерах
вторичного тока небаланса от тока небаланса фильтра токов нулевой
последовательности сложно. В случае если несимметрия возникает в разных
фазах или изменения емкостей неодинаковы по величине, напряжение
нулевой последовательности отлично от нуля и в принципе это может
привести к срабатыванию защиты от ОЗЗ.
0 = 0, но отличить его при замерах
вторичного тока небаланса от тока небаланса фильтра токов нулевой
последовательности сложно. В случае если несимметрия возникает в разных
фазах или изменения емкостей неодинаковы по величине, напряжение
нулевой последовательности отлично от нуля и в принципе это может
привести к срабатыванию защиты от ОЗЗ.
Приведенный выше пример объясняет тот факт, что иногда при повторных
замерах небаланса на выходе фильтра токов нулевой последовательности,
проведенных через незначительный промежуток времени, величина
замеренного тока может существенно отличаться. Видимо, в сети появилась
новая несимметрия.
НЕБАЛАНС, СВЯЗАННЫЙ С НЕСИММЕТРИЕЙ ФАЗНЫХ ЭДС ИСТОЧНИКА ПИТАНИЯ
Из-за несимметрии фазных
напряжений на шинах питающей подстанции на изолированной
(резистивно-заземленной, компенсированной) нейтрали сети может
появиться напряжение несимметрии [1]. Рассматриваемая ситуация
относится, например, к случаю, когда секция сборных шин питается
непосредственно от генератора (а остальные присоединения сборных шин
имеют симметричные относительно земли сопротивления).
Возможен и другой вариант: секция шин питается от трансформатора
(остальные присоединения также симметричны и не могут привести к
«смещению» нейтрали).
Получим в общем виде выражение для определения напряжения смещения
нейтрали в резистивно-заземленной сети при несимметричной системе ЭДС.
При этом будем считать, что параметры сети симметричны и фазные емкости
равны СА = СВ = СС = СФ. В качестве основной примем ЭДС фазы А  A. После соответствующих преобразований в
(1) получим:
A. После соответствующих преобразований в
(1) получим:
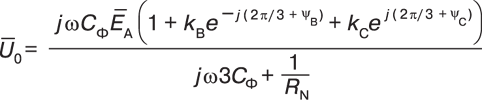 (4)
(4)YB, YC– фазы, учитывающие возможные отклонения ЭДС по углу.
Определим теперь величину токов нулевой последовательности, протекающих в «симметричных» линиях (с одинаковыми сопротивлениями по фазам) при несимметричных фазных напряжениях на шинах питающей подстанции.
Рассмотрим для примера схему сети с одной ЛЭП на рис. 1.
Ток нулевой последовательности в этой линии, возникающий за счет напряжения
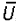 0 в нейтрали, определится как сумма токов
трех фаз:
0 в нейтрали, определится как сумма токов
трех фаз:3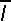 0 =
0 = 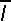 A +
A + 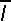 B +
B + 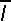 C = (
C = ( A –
A – 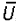 0)
0) 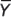 A + (
A + ( B –
B – 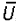 0)
0)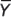 B + (
B + ( C –
C – 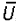 0)
0)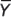 C .
C .
После несложных преобразований получим:
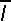 0 =
0 = 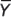 Ф (
Ф ( Э.НЕС – 3
Э.НЕС – 3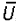 0),
(5)
0),
(5)
где 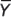 Ф = jwCФ –
фазная емкостная проводимость;
Ф = jwCФ –
фазная емкостная проводимость;
 Э.НЕС =
Э.НЕС =  A +
A +  B +
B +  C – эквивалентная ЭДС при
наличии несимметрии.
C – эквивалентная ЭДС при
наличии несимметрии.
Выражение для определения напряжения нулевой последовательности  0, вызванного несимметрией ЭДС, можно записать в
следующем виде:
0, вызванного несимметрией ЭДС, можно записать в
следующем виде:
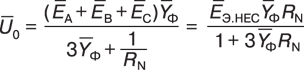 (6)
(6) (7)
(7)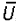 0 в нейтрали, вызванного этой
несимметрией, к сопротивлению заземляющего резистора RN. С учетом того,
что активный ток резистора совпадает по фазе с приложенным к нему
напряжением
0 в нейтрали, вызванного этой
несимметрией, к сопротивлению заземляющего резистора RN. С учетом того,
что активный ток резистора совпадает по фазе с приложенным к нему
напряжением 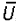 0, направление активного тока в линии
противоположно этому напряжению (этот ток протекает по направлению к
шинам).
0, направление активного тока в линии
противоположно этому напряжению (этот ток протекает по направлению к
шинам).
При наличии нескольких ЛЭП, питающихся от одной секции шин, активный ток резистора будет распределяться по линиям пропорционально величинам их емкостей, то есть величина тока в каждой из ЛЭП составит:
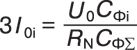 (8)
(8)CФS – суммарная фазная емкость сети.
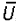 на шинах (нет пути для протекания этих
токов). Выше уже отмечалось, что при несимметрии фазных сопротивлений
сети возможен обратный случай, когда при отсутствии напряжения
на шинах (нет пути для протекания этих
токов). Выше уже отмечалось, что при несимметрии фазных сопротивлений
сети возможен обратный случай, когда при отсутствии напряжения 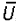 на шинах в линиях протекают токи нулевой
последовательности. Это говорит о том, что небалансы по токам и
напряжениям нулевой последовательности в некоторых случаях могут
присутствовать по отдельности.
на шинах в линиях протекают токи нулевой
последовательности. Это говорит о том, что небалансы по токам и
напряжениям нулевой последовательности в некоторых случаях могут
присутствовать по отдельности.
Непросто ответить на вопрос о том, какое численное значение неравенства ЭДС необходимо учитывать при расчетах рассматриваемой составляющей небаланса. По-видимому, это зависит от ряда обстоятельств:
- на каких сборных шинах определяется небаланс (питающихся непосредственно от генератора или «удаленных», отделенных от генератора на один или большее количество трансформаторов);
- схемы и параметров «предшествующей» питающему трансформатору сети;
- разновидности и параметров генераторов, питающих сеть, а также их нагрузки;
- параметров питающего трансформатора и т.д.
НЕБАЛАНС, ВЫЗВАННЫЙ НЕСИММЕТРИЕЙ ФАЗНЫХ НАГРУЗОК
Как правило, в российских сетях
6–35 кВ отсутствуют нагрузки, имеющие непосредственную связь
с землей, поэтому небаланс, вызванный неравенством фазных
токов таких нагрузок, не рассматриваем.
Из-за несимметрии нагрузок в сети 0,4 кВ могут возникнуть разные токи в
фазах сети высшего напряжения, которые могут привести к смещению
нейтрали понижающих трансформаторов.
Если нейтраль понижающего трансформатора не заземлена, то такое
смещение не приводит к небалансу по напряжениям и токам нулевой
последовательности в сети 6–35 кВ. Однако установка
заземляющих резисторов в нейтралях понижающих трансформаторов (как,
например, это описано в [2]) приводит к тому, что смещение их нейтралей
вызывает появление дополнительного небаланса токов Iнб.нагр. и
напряжений Uнб.нагр. нулевой последовательности.
В следующей статье авторы предполагают рассмотреть порядок выбора
уставок и проверки чувствительности направленных защит нулевой
последовательности от замыканий на землю.
Литература
1. Кадомская К.П., Лавров Ю.А.,
Рейхердт А.А. Перенапряжения в электрических сетях различного
назначения и защита от них: Учебник. – Новосибирск: Изд-во
НГТУ, 2004. – 368 с.
2. Шалин А.И. Защиты от замыканий на землю в сетях 6–35 кВ.
Пример расчета уставок // Новости ЭлектроТехники. – 2005.
– № 4 (34).