Вернуться в библиотеку
УДК 66.011:532.555
Ошовский В.В., Охрименко Д.И., Сысоев А.Ю. (ДонНТУ)
ИСПОЛЬЗОВАНИЕ КОМПЬЮТЕРНЫХ СИСТЕМ КОНЕЧНО-ЭЛЕМЕНТНОГО АНАЛИЗА ДЛЯ МОДЕЛИРОВАНИЯ ГИДРОДИНАМИЧЕСКИХ ПРОЦЕССОВ
Источник: Наукові праці ДонНТУ. Cepія: Хімія i хімічна технологія, 2010. – Вип. 15(163). – С. 163-173.
В данной статье рассмотрены основные принципы постановки и решения гидродинамических задач на примере анализа сужающего устройства – диафрагмы. В технологической практике диафрагма используется при замерах объемных скоростей технологических потоков. Эта методика может быть использована студентами технических специальностей при выполнении курсовых и дипломных проектов.
Ключевые слова: моделирование, конечно-элементный анализ, гидродинамические процессы, сужающие устройства, диафрагма.
Студентами химиками-технологами в курсе базовой подготовки приходится часто сталкиваться с задачами гидродинамики, например, при изучении курса процессов и аппаратов химической технологии. При всей своей распространенности вопросы гидродинамики имеют сложный характер, как в теоретическом, так и в реализационном аспекте.
В общем случае для описания движения вязкой ньютоновской жидкости применяются уравнения Навье-Стокса. Система состоит из уравнений движения и уравнений неразрывности.
В векторном виде для несжимаемой ньютоновской жидкости они записываются следующим образом:

где η – динамическая вязкость, Па·с; ρ – плотность, кг/м3; .jpg) – векторное поле скоростей, м/с; p – давление, Па; – векторное поле скоростей, м/с; p – давление, Па; .jpg) – векторное удельное силовое поле, Н/м3; t – время, с [1]. – векторное удельное силовое поле, Н/м3; t – время, с [1].
В гидродинамике выделяют два основных типа течения жидкостей – ламинарное и турбулентное. Особые трудности для изучения и моделирования вызывает именно турбулентное течение.
Турбулентность – название такого состояния сплошной среды, газа, жидкости, их смесей, когда в них наблюдаются хаотические колебания мгновенных значений давления, скорости, температуры, плотности относительно некоторых средних значений, за счёт зарождения, взаимодействия и исчезновения в них вихревых движений различных масштабов, а также линейных и нелинейных волн, струй. Турбулентность возникает, когда число Рейнольдса превышает некое критическое значение. Моделирование турбулентности – одна из наиболее трудных и нерешённых проблем в гидродинамике и теоретической физике.
В настоящий момент создано большое количество разнообразных моделей для расчёта турбулентных течений. Они отличаются друг от друга сложностью решения и точностью описания течения. Основная идея моделей сводится к предположению о существовании средней скорости потока и среднего отклонения от него: u = uср+ u'. После упрощения уравнений Навье-Стокса, в них помимо неизвестных средних скоростей появляются произведения средних отклонений u'iu'j. Различные модели по-разному их моделируют [2].
COMSOL Multiphysics – это интерактивная среда для моделирования большинства научных и инженерных задач основанных на дифференциальных уравнениях в частных производных методом конечных элементов. Этот пакет позволяет моделировать гидродинамические, теплофизические, массообменные и другие процессы.
Для решения разнотипных гидродинамических задач в COMSOL Multiphysics предусмотрены такие уравнения и модели:
- уравнения Навье-Стокса для несжимаемой жидкости;
- уравнения Навье-Стокса для слабосжимаемой жидкости (в уравнение неразрывности входит плотность жидкости (газа), т.е. считается, что плотность жидкости (газа) есть величина непостоянная, а функция некоторых переменных, зачастую, температуры);
- k-ε модель турбулентности (вместе с уравнениями Навье-Стокса решаются два дополнительных уравнения для транспорта кинетической энергии турбулентности и диссипации турбулентности);
- k-ω модель турбулентности (вместе с уравнениями Навье-Стокса решаются два дополнительных уравнения для транспорта кинетической энергии турбулентности и скорости диссипации турбулентной энергии)
Последние две модели базируются на осредненных по Рейнольдсу уравнениях Навье-Стокса (RANS).
COMSOL Multiphysics использует обобщенную версию уравнений Навье-Стокса:

где I – единичный тензор;  – тензор вязких напряжений, Па. – тензор вязких напряжений, Па.
Учитывая сложность уравнений турбулентных моделей, они здесь не приводятся. Стоит отметить только, что для решения одних задач лучше подходят модели турбулентности, а для других – уравнения Навье-Стокса. Все зависит от типа поставленной задачи.
В качестве примера ниже представлена методика расчета сужающего устройства – диафрагмы, выбор которой является одной из часто встречающихся задач при выполнении студентами химиками-технологами расчетных и курсовых работ. Основные характеристики диафрагмы:
| |
Технологическое вещество |
|
вода; |
| |
Температура технологического вещества |
|
20°С; |
| |
Диаметр трубы |
|
D = 0,03 м; |
| |
Диаметр отверстия диафрагмы |
|
d0 = 0,024 м; |
| |
Толщина диафрагмы |
|
δ = 0,002 м; |
| |
Потеря давления на участке трубопровода с диафрагмой
(при средней скорости потока 1,4 м/с) |
|
900 Па [3]. |
Для создания и расчета любой задачи рекомендуется следующая последовательность действий:
-
Выбрать размерность модели, определить физический раздел в Model Navigator (Навигатор моделей) и определить стационарный или нестационарный анализ процесса.
- Определить рабочую область и задать геометрию.
- Задать исходные данные, зависимости переменных от координат и времени.
- Указать физические свойства и начальные условия.
- Указать граничные условия (ГУ).
- Задать параметры и построить сетку конечных элементов.
- Определить параметры блока решения и запустить расчет.
- Настроить режим отображения.
- Получить результаты [4].
1. Навигатор моделей
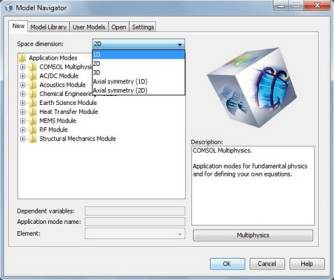
Размерность модели выбирается в окне Model Navigator (Навигатор моделей) (рис. 1). На первой вкладке New в раскрывающемся списке Space Dimension (Размерность пространства), кроме 1D, 2D и 3D можно выбрать Axial Symmetry (1D) и (2D) для осесимметричных задач.
|
Рис. 1. Выбор размерности пространства
и физического раздела
|
В этом окне также находится вкладка Model Library (Библиотека моделей), которая содержит большое количество моделей-примеров. На вкладке Open (Открыть) можно выбрать модель из дерева каталогов. Для открытия модели рекомендуется именно этот способ, т.к. здесь есть возможность предварительного просмотра содержимого файла.
Задать решение гидродинамической задачи в COMSOL Multiphysics можно несколькими способами:
- Application Modes → COMSOL Multiphysics → Fluid Dynamics → Incompressible Navier-Stokes
- Application Modes → Chemical Engineering Module → Momentum Transport
- Application Modes → Chemical Engineering Module → Flow with Variable Density
- Application Modes → Earth Science Module → Fluid Flow
- Application Modes → Heat Transfer Module → Weakly Compressible Navier-Stokes (k-ε Turbulence Model, k-ω Turbulence Model)
- Application Modes → MEMS Module → Microfluidics
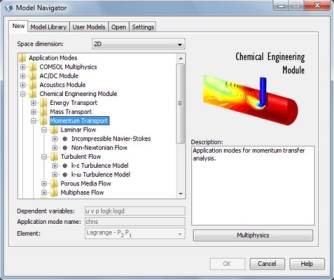
Как видно способов задания течения жидкости много, однако большинство из них повторяются в разных прикладных модулях. При этом в разных модулях используются различные модели переноса импульса. Наиболее полно течения жидкостей раскрыты в Chemical Engineering Module. Рекомендуется использовать именно этот модуль для решения гидродинамических задач (рис. 2).
Важной особенностью гидродинамических задач в COMSOL Multiphysics является невозможность их решения при
|
Рис. 2. Уравнения переноса импульса в
Chemical Engineering Module
|
размерности пространства 1D. Такие задачи решаются только при размерностях пространства 2D, 3D и Axial Symmetry (2D). Для решения осесимметричных задач рекомендуется использовать режим Axial Symmetry (2D) – это экономит ресурсы вычислительной машины и открывает дополнительные возможности анализа результатов, например, расчет поверхностных интегралов.
После выбора модели можно сразу определить будет ли задача стационарной или нестационарной. Задается это для каждого из подразделов (Steady-state analysis (Стационарный анализ) и Transient analysis (Переходный анализ)). Впрочем, вид анализа можно потом изменить.
После нажатия клавиши OK в Model Navigator открывается окно основной программы с рабочей областью. При необходимости решения мультифизической задачи, например, решение конвективного теплопереноса с учетом поля скоростей, необходимо нажать кнопку Multiphisics, затем нажимается кнопка Add geometry (Добавить геометрию), в открывшемся окне выбирается размерность и названия осей.
После выбора геометрии, нажимается кнопка Add…(Добавить) и сначала выбирается один физический раздел (Heat Transfer → Convection and Conduction), а потом в модель добавляется второй раздел (Fluid Dynamics → Incompressible Navier-Stokes). Между собой они взаимодействуют как раз через поле скоростей.
В списке Application Modes необходимо выбрать режим Chemical Engineering Module → Momentum Transport → Turbulent Flow → k-ε Turbulence Model и нажмем кнопку OK.
2. Рабочая область и задание геометрии
Следующим этапом является создание расчетной геометрии. Главное меню:
File – содержит команды создания, открытия и сохранения файлов, печати, а также импорта геометрии из внешних САПР и экспорта полученных данных в текстовый файл. Для создания рисунка модели, который будет показываться на вкладке Open (Открыть) Навигатора моделей следует использовать пункт меню Save Model Image.
Edit – содержит команды отмены и повторения операций, работы с буфером обмена и команды выделения.
Options – содержит команды задания рабочей области Axes/Grid settings, констант Constants, выражений Expression, функций Function, связанных переменных Coupling Variables и различные настройки отображения геометрических элементов и масштаба.
Draw – содержит команды построения и преобразования геометрических объектов, а так же команды превращения двумерных объектов в трехмерные. Режим задания геометрии имеет ограниченные функциональные возможности, поэтому рекомендуется создавать модель заранее во внешних САПР.
Physics – содержит команды задания физических свойств подобластей Subdomain Settings, граничных условий Boundary Settings, в том числе периодических граничных условий Periodic Condition и изменения системы дифференциальных уравнений Equation system. Используя Properties… можно не покидая рабочую область перейти от расчета стационарной задачи к нестационарной, выбрать турбулентную модель, перейти от расчета однофазных течений к двухфазным.
Mesh – содержит команды управления сеткой конечных элементов. Здесь можно задать размер конечных элементов,

|
|
Рис. 3. Геометрия модели
|
коэффициент роста элементов в подобласти, тип сетки.
Solve – содержит очень важные команды управления блоком решения, можно выбрать зависимость от времени, линейность или нелинейность, а так же указать множество других параметров решения. Используя Solver Manager… → Store Solution можно запоминать полученное решение и затем использовать его в качестве начальных условий для другой задачи.
Postprocessing – содержит команды для отображения результатов вычислений, во всех возможных видах: от векторов и поверхностей уровня, до графиков и интегралов по границе.
Multiphisics – открывает Model Navigator и позволяет переключаться между физическими режимами в мультифизических моделях или добавить новые.
Help – содержит обширную справочную систему. Если геометрия уже создана с помощью внешней САПР (например, AutoCAD, КОМПАС), то необходимо выполнить следующие действия: пункт меню File → Import → CAD Data From File.
Что является актуальным, поскольку студентами химиками-технологами изучается ряд курсов по применению систем автоматизированного проектирования.
Выбирается нужный файл и нажимается кнопка Import. В окне появится эскиз диафрагмы. На левой панели необходимо нажать пиктограмму Coerce to Solid. Это обеспечит создание сплошной двухмерной поверхности сечения диафрагмы (рис. 3).
3. Функции, константы и выражения
Параметры потока могут зависеть от температуры и координат, внешние воздействия могут описываться различными функциями, зависящими от времени и множества других переменных. В данном пакете существует мощный инструментарий для работы с константами и функциями. Большинство этих команд находится в меню Options. Рассмотрим некоторые из них.
Constants (Константы). Рекомендуется все применяемые в модели константы вынести в эту таблицу, а во всех формулах задавать только буквенное обозначение. Например, задать температуру воды Т_water=30 (или давления на границах, диаметр труб и т.д.) и во всех уравнениях и условиях вместо цифры задавать Т_water. Тогда в случае необходимости можно поменять одну цифру, а не менять по всем уравнениям и условиям температуру воды. Так же список всех часто употребляемых констант можно сохранить в отдельный файл и переносить из модели в модель. В программе существует возможность к каждой константе написать Description (Примечание), при работе нескольких человек с одной моделью не стоит игнорировать эту графу.
Expression (Выражения) содержит Scalar expression (Скалярные выражения), Subdomain, Boundary, Edge (только в трехмерном режиме) и Point expression. Можно задать зависимость какого-либо параметра от времени t; координат x, y, z; от безразмерной координаты s (изменяется от 0 до 1 по длине каждой границы) или от любых других вычисляемых параметров, например, распределение скоростей жидкости в поперечном сечении на входной границе можно определить как Umax*4*s*(1-s). У различных элементов системы очень часто одни и те же параметры определяются по разным законам. Есть возможность задать одно имя у переменной, например alfa. И открыв Boundary expression (Граничные выражения) задать для разных границ, различные формулы вычисления alfa. Тогда для всех границ можно будет задать коэффициент alfa, а программа сама подставит для каждой границы соответствующую формулу.
Material/Coefficients Library (Библиотека материалов), содержит большое количество функций для различных веществ. Можно задать любые физические свойства веществ, и их зависимость от параметров (температуры и давления). Эта встроенная база данных может использоваться будущими инженерами химико-технологических специальностей в качестве справочника по физическим свойствам различных материалов.
Для данной задачи в окне Constants следует задать следующие константы: T=20[degC] (температура воды), Patm=101325[Pa] (давление на выходе), Pin=Patm+900[Pa] (давление на входе), D=0.03[m] (диаметр трубы).
4. Задание свойств жидкости и начальных условий
Когда геометрия задана и все константы определены, можно приступить к заданию свойств жидкости. Для этого нужно открыть диалоговое окно Physics → Subdomain Settings. На вкладке Physics задаются плотность, вязкость и объемная сила. Можно воспользоваться библиотекой материалов для выбора необходимого вещества, при этом описанные поля заполняются автоматически встроенными функциями. Положительное направление составляющих вектора объемной силы совпадает с направлением соответствующих осей. Т.е. при задании гравитационной силы, которая направлена вниз (против оси y) в поле Fy необходимо записать „-g*rho_chns”, g можно задать в Constants (Константы) равной 9,81 м/с2 – ускорение свободного падения, а функция rho_chns (если название прикладного режима не chns, то необходимо записать имя данного приложения) автоматически подставляет расчетное значение плотности.
Метод конечных элементов подразумевает дискретизацию пространства. При моделировании явлений переноса в
|
|
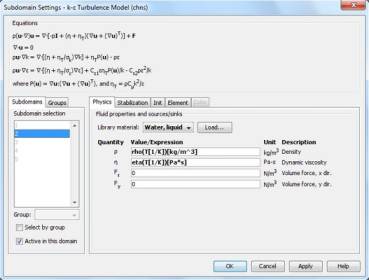
Рис. 4. Окно настройки подобласти
|
сложных объектах это может привести к нестабильности решения. В COMSOL Multiphysics предусмотрены специальные механизмы для численной стабилизации решения. Методы стабилизации решения основаны на добавлении малых слагаемых в дифференциальные уравнения. На вкладке Stabilization можно задать коэффициенты соответствующих уравнений. Вкладка Init предназначена для задания начальных условий. Если задача стационарная, то на этой вкладке не нужно ничего задавать. Однако следует отметить, что в некоторых случаях необходимо задать давление, т.к. оно может использоваться при расчете начального приближения и в случае отрицательных чисел может выдаваться ошибка. Вкладка Element позволяет выбрать вид конечных элементов.
В окне Subdomain Settings нужно отметить подобласти с номерами 1, 3, 4, 5 и снять галочку в поле Active in this domain. Затем нажать Apply. Так как эти подобласти являются стенками труб и частью диафрагмы, то они не описываются уравнениями гидродинамики. Необходимо выделить подобласть 2 и нажать на кнопку Load… В появившемся окне выбирается Liquids and Gases → Liquids → Water, liquid и нажимается OK. Гравитационное поле не учитывается, поэтому сразу необходимо нажать OK и закрыть окно настройки свойств жидкости (рис. 4).
5. Задание граничных условий
Очень важно правильно задать граничные условия. Ниже приведены типы граничных условий в приложении Incompressible Navier-Stokes (табл. 1). Граничные условия задаются в окне Physics → Boundary Settings.
Таблица 1. Некоторые типы граничных условий
| Типы ГУ в COMSOL Multiphysics |
Русскоязычный аналог |
- Wall
- No slip (Default)
- Slip
- Sliding wall
- Moving/leaking wall
- Inlet
- Velocity (Default)
- Pressure, no viscous stress
- Laminar inflow
- Outlet
- Velocity
- Pressure
- Pressure, no viscous stress (Default)
- No viscous stress
- Normal stress
- Laminar outflow
- Symmetry boundary
- Symmetry (Default)
- Axial symmetry
- Open boundary
- Normal stress (Default)
- No viscous stress
- Stress
- General stress (Default)
- Normal stress
- Normal stress, normal flow
|
- Стенка
- Условие прилипания (умолчание)
- Скольжение (без прилипания)
- Скользящая стенка
- Передвигающаяся/пористая стенка
- Вход
- Скорость (умолчание)
- Давление, нет вязких напряжений
- Ламинарный приток
- Выход
- Скорость
- Давление
- Давление, нет вязких напряжений (умолчание)
- Нет вязких напряжений
- Нормальные напряжения
- Ламинарный отток
- Граница симметрии
- Симметрия (умолчание)
- Осевая симметрия
- Открытая граница
- Нормальные напряжения (умолчание)
- Нет вязких напряжений
- Напряжение
- Общие напряжения (умолчание)
- Нормальные напряжения
- Нормальные напряжения, нормальный поток
|
При выборе соответствующих условий программа автоматически задает необходимые уравнения, нужно только задать коэффициенты этих уравнений.
Входные границы для моделей турбулентности описываются таким же образом, как и для уравнений Навье-Стокса. В дополнении, должны быть установлены значения для двух турбулентных чисел (k и ε, или k и ω). В качестве альтернативы можно задать масштаб турбулентности (LT) и интенсивность турбулентности (IT). Значение ниже 0,1% – это низкая интенсивность. Хорошие аэродинамические трубы могут производить значения IT около 0,05%. Полностью турбулентные потоки имеют интенсивности между 5 и 10 процентами.
Масштаб турбулентности – это критерий величины вихрей, которые не распались. Для свободных потоков это значение обычно очень мало (порядка сантиметров). Этот масштаб не может быть равным нулю, так как это подразумевает бесконечно большое рассеяние (диссипацию). Можно использовать таблицу 2, которая приводится в [5], как рекомендацией при задании LT:
Таблица 2. Масштаб турбулентности для двумерных течений
| Тип потока |
LT |
L |
| Смешанный слой |
0,07L |
Ширина слоя |
| Плоская струя |
0,09L |
Ширина половины струи |
| Турбулентный след |
0,08L |
Ширина турбулентного следа |
| Осесимметричная струя |
0,075L |
Ширина половины струи |
Пограничный слой (∂p/∂x = 0)
– вязкий подслой
– наружный слой |
κlw·(1-exp(-lw+/26))
0,09L |
Толщина пограничного слоя |
Трубы и каналы
(полностью развитый поток) |
0,07L |
Диаметр трубы или ширина канала |
Где lw это расстояние до стенки и lw+ = lw / l* это расстояние до стенки в единицах вязкости, κ – постоянная Кармана (0,42), l* – масштаб вязкости.
Правильный выбор масштаба турбулентности является важным моментом при решении гидродинамических задач на основе k-ε турбулентной модели, поскольку неверное задание его приводит к невозможности корректного решения.
Необходимо задать следующие граничные условия в окне Boundary Settings (табл. 3). Условия на остальных границах остаются без изменения.
Таблица 3. Граничные условия
| Номер границы |
Тип условий |
Значения |
| 3 |
Inlet;
Pressure, no viscous stress |
Pin; 1; 0,07*D; 0,05 |
| 19 |
Outlet;
Pressure, no viscous stress |
Patm |
6. Построение сетки
После задания всех свойств и граничных условий наступает очередь построения сетки конечных элементов. Для простейших моделей, на первом этапе оценочного расчета можно задать сетку по умолчанию Mesh → Initialize Mesh (или пиктограмма с изображением треугольника) и несколько раз нажать Mesh → Refine mesh и получив достаточно мелкую сетку приступить к решению. Для более мелких элементов модели система автоматически произведет сгущение сетки, а если необходимо в какой-либо части системы еще более сгустить сетку, то можно нажать кнопку Refine selection и указать нужную область. В меню Mesh → Free Mesh Parameters также можно выбрать один из предустановленных режимов или
|
|
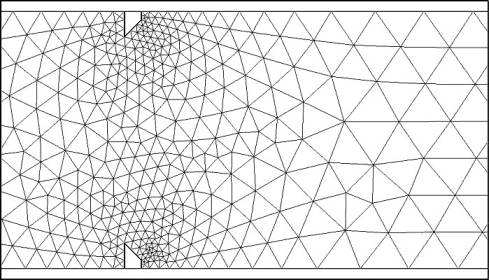
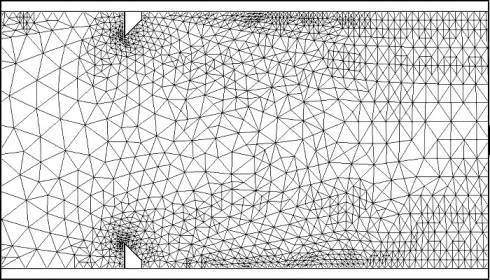
Рис. 5. Первоначальная сетка
|
Рис. 6. Адаптированная сетка
|
увеличить число элементов на каждой границе, темп роста элементов по подобласти, максимальный размер элемента и т.д.
В COMSOL Multiphysics существует метод решения с адаптивной сеткой. После предварительного расчета на исходной сетке система в зависимости от локального градиента искомой функции перестраивает сетку – в местах с большими градиентами сетка уменьшается, а с малыми, соответственно укрупняется. Поставленная задача решается данным методом.
В окне Mesh → Free Mesh Parameters следует выбрать режим Extra fine и нажать на кнопку Remesh. Первоначальная сетка и адаптированная в области диафрагмы показаны на рисунках 5 и 6.
Правильный выбор вида расчетной сетки конечных элементов является определяющим моментом в решении задач. В некоторых случаях правильность и принципиальная возможность решения определяется опытом построения сетки для конкретных объектов.
7. Процедура решения
Выбор решающего алгоритма и его параметров очень важен, так как в основном от него зависит достоверность вычислений. Неправильная настройка может привести к грубым ошибкам решения, которые очень трудно выявить.
Кнопка Solve или пункт меню Solve → Solve problem запускает алгоритм решения с текущими настройками. Кнопка Restart или пункт меню Solve → Restart перезапускает алгоритм решения, используя текущие значения (поле скоростей, давлений и т.д.) как начальные. Для изменения параметров необходимо выбрать Solve → Solver parameters… или соответствующую кнопку. В открывшемся окне, если стоит галочка Auto select solver, значит программа в зависимости от прикладного режима подобрала наиболее подходящее устройство, для несложных вычислений чаще всего менять его не надо. Если задача стационарна, то необходимо определить линейная она или нелинейная. Гидродинамические задачи, как правило, нелинейные.
В COMSOL Multiphysics существует два типа решающих алгоритмов – прямые и итерационные. Для обоих типов по умолчанию стоит небольшое число итераций. Рекомендуется увеличить его хотя бы до 500 во избежание преждевременной остановки правильно работающего решающего алгоритма.
Следует открыть окно Solve → Solver parameters… и отметить маркером пункты Adaptive mesh refinement и Plot while solving. Последний пункт позволяет следить за ходом вычислительного процесса во время расчета. Рекомендуется использовать эту опцию в качестве элемента контроля решения задачи. После задания свойств нажать кнопку Solve или команду Solve → Solve Problem.
При начальном освоении пакета студентами рекомендуется использование решающего алгоритма выбранного автоматически. Что в дальнейшем, при накоплении опыта, может быть заменено на более сложный алгоритм решения.
8. Визуализация результатов
|
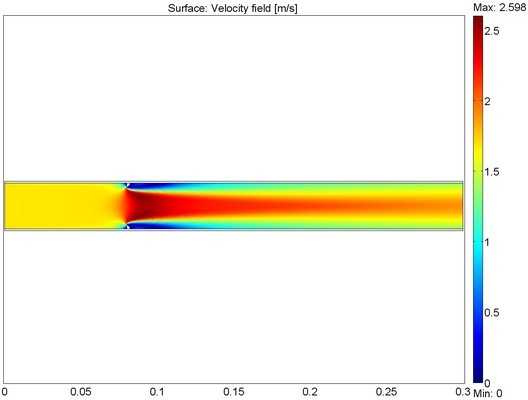
Рис. 7. Поле скоростей, выводимое по
умолчанию
|
После завершения решения автоматически включается режим Postprocessing mode (Режим постобработки) в котором можно наблюдать результаты вычисления. Вручную этот режим можно включить соответствующей кнопкой или командой Postprocessing → Postprocessing mode. По умолчанию, в расчетах по уравнению Навье-Стокса выводится поле скоростей (рис. 7).
На вкладке General в поле Plot type необходимо выбрать, какие параметры результатов вычисления будут отображаться.
В поле Solution to use (Использование решения) в режиме переходного анализа можно выбрать временной слой (по умолчанию, изображается последний) в раскрывающемся списке Solution at time (Решение для времени).
Surface – выводит значение скалярного поля заданной функции в цветовом виде. На вкладке Streamline можно вывести линии тока. Contour – выводит решение в виде изолиний. Arrow plot – выводит векторное поле заданной функции в виде стрелок.

|
|
Рис. 8. Линии тока в области диафрагмы
|
Рассмотрим линии тока в области диафрагмы (рис. 8). Видно образование симметричного вихревого течения за плоскостью диафрагмы. Таким образом, полученные результаты дают возможность студентам визуально наблюдать

|
|
Рис. 9. Изобары относительных давлений
|
застойную зону в области сужающего устройства. Именно это является причиной пониженного давления в этой области. Для их построения на вкладке Streamline выбирается в раскрывающемся списке Predefined quantities параметр Velocity field. На вкладке Start Points в поле Number of start points необходимо набрать 40.
Для построения изобар относительных давлений (рис. 9) на вкладке Contour в поле Expression необходимо ввести p-Patm. Number of levels – 20; Labels отметить маркером, после чего нажать OK. Для построения графиков зависимостей давления по оси потока и у нижней стенки (рис. 10 и 11) необходимо проделать следующие операции. Открыть окно Сross-Section Plot Parameters

|
|
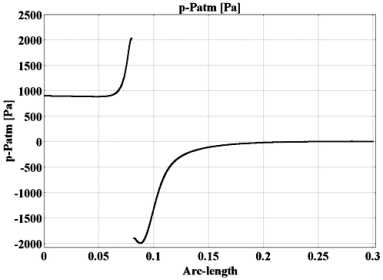
Рис. 10. Распределение давления по оси потока
|
Рис. 11. Распределение давления по внутренней
стенке трубы
|

|
|
Рис. 12. Объединенный график давлений
|
в меню Postprocessing. На вкладке Line/Extrusion в поле Expression ввести p-Patm, а в рамке Сross-Section line data ввести следующие цифры, OK:
| x0:0; x1:0.3; y0:0; y1:0; |
Line resolution:500 – по оси потока; |
| x0:0; x1:0.3; y0:-0.015; y1:-0,015; |
Line resolution:500 – по внутренней стенке. |
Для построения объединенного графика (рис. 12) необходимо сначала построить одну зависимость, затем на вкладке General выделить маркером Keep current plot, а потом построить второй график.
Анализ графиков распределения давления по сечению трубы и по внутренней ее стенке дает возможность говорить о скачкообразном перепаде давления. На периферии потока наблюдается резкое увеличение давления перед диафрагмой и его значительное понижение в области вихревого течения.
Использование этого эффекта лежит в основе метода измерения расходов жидких и газообразных технологических веществ.
Выводы
Конечно-элементный метод расчета применим для широкого класса химико-технологических задач. Этот метод в полной мере реализован в программной системе COMSOL Multiphysics, что дает возможность применения данного пакета студентами при выполнении инженерных расчетов.
Широкое внедрение метода конечных элементов позволяет студентам более глубоко проникнуть в суть гидродинамических и теплофизических процессов, получить не только численное решение, но и наглядную визуализацию особенностей изучаемых явлений.
Литература
1. Кутепов А.М., Полянин А.Д., Запрянов З.Д., Вязьмин А.В., Казенин Д.А. Химическая гидродинамика: Справочное пособие. – М.: Квантум, 1996. – 336 с.
2. Дытнерский Ю.И. Процессы и аппараты химической технологии: Учебник для вузов. Изд. 2-е. В 2-х кн.: Часть 1.Теоретические основы процессов химической технологии. Гидромеханические и тепловые процессы и аппараты. – М.: Химия,1995. – 400 с.: ил.
3. Павлов К.Ф., Романков П.Ф., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. – Л.: Химия, 1987. – 576 с., ил.
4. Егоров В.И. Применение ЭВМ для решения задач теплопроводности. Учебное пособие. – СПб: СПб ГУ ИТМО, 2006. – 77 с.
5. Chemical Engineering Module. User’s Guide. – Version: November 2008, COMSOL 3.5a.
© Ошовский В.В., Охрименко Д.И., Сысоев А.Ю., 2010
|




