УДК 622.232.32

К библиотеке

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАБОЧЕГО ПРОЦЕССА ГИДРАВЛИЧЕСКОГО УДАРНОГО МЕХАНИЗМА

Устименко Т.А., канд.техн.наук, Кононенко А.П., докт.техн.наук, Селивра С.А., канд..техн.наук, Яценко А.Ф.,канд..техн.наук, Донецкий национальный технический университет

Источник: Наукові праці Донецького національного технічного університету. Серія «Гірничо-електромеханічна». Випуск 16(142).-Донецьк: ДонНТУ, 2008 с.258-264(фахове видання)

Исследована одна из принципиальных схем гидравлического ударного механизма, составлена математическая модель рабочего процесса, содержащая дифференциальные уравнения движения основных звеньев. Путем сравнения данных, полученных в результате моделирования и натурного эксперимента, доказана адекватность разработанной математической модели .

One of the percussion mechanisms schematic circuit was reseached, mathematical model was created. It includes differentials equations main elements movement. It was proved model adequacy to the full-scale experiment.

Проблема и ее связь с научными или практическими задачами. Разработка эффективного инструмента для механизации трудоемких операций по разрушению массива в строительстве, металлургии, угольной промышленности является актуальной задачей. Особенно перспективным является гидравлический инструмент. Если гидравлические механизмы (в основном импортного производства) находят достаточно широкое применение в качестве навесного оборудования, то разработка ручного инструмента является достаточно перспективным направлением.

Анализ исследований и публикаций. Известны несколько подходов по классификации, выделению и исследованию различных структурных схем гидравлических механизмов ударного действия [1,2]. Исследованию работы гидравлических ударных механизмов посвящены работы, в которых рассматриваются устройства c различной управляемостью камер. Однако в данных работах не рассматривается динамика управляющего звена совместно с движением узла ударника.

Постановка задачи. Гидравлический ударный механизм отбойного молотка, работающий в системе объемного гидропривода представляет собой сложную гидродинамическую систему, которая характеризуется большим числом (более 20) факторов. Для всестороннего исследования ее функционирования, выбора основных конструктивных и рабочих параметров, для выявления рациональных режимов, необходимо проведение большого числа экспериментов. Причем проведение каждого опыта будет сопряжено с изготовлением отдельных узлов и деталей устройства. Наиболее эффективным путем решения является математическое, а точнее, имитационное моделирование рабочего процесса установки. В связи с этим ставится задача математического описания рабочего процесса одной из принципиальных схем гидроударного механизма, с целью разработки имитационного алгоритма и программы. Данный подход позволит исследовать большой объем вариантов и произвести выбор оптимальных параметров системы без проведения трудоемких экспериментов.

Изложение материала и результаты. Рассматриваемая принципиальная схема гидроударного механизма приведена на рис.1. На схеме указаны основные узлы устройства: I – узел ударника с рабочим инструментом 1 и поршнем-бойком 2; II – узел управления с поршнем-клапаном 3, а также гидропневмоаккумулятор (ГПА) гидроударного механизма 4 и элементы гидроэнергетического снабжения: насос объемного принципа действия 6 с предохранительным клапаном 7 и емкостью для рабочей жидкости 8, ГПА 9 и напорной магистралью 5, т.е. основные структурные звенья системы, математические модели которых будут построены. При разработке математической модели были приняты следующие допущения:

• во входном сечении напорной магистрали предполагается постоянный расход рабочей жидкости;

• массы подвижных элементов (поршня-бойка и поршня-клапана) предполагаются сосредоточенными;

• волновые процессы в соединительных каналах не учитываются, гидравлические сопротивления каналов считаются сосредоточенными у соответствующих камер;

• изменения значений давления и объема воздуха в ГПА подчиняется адиабатному закону;

• утечки жидкости в системе отсутствуют;

• волновые процессы, происходящие в рабочем инструменте и бойке не учитываются.

На рис.1 указаны направления расходов, выбранные для математического описания процесса. Основным является узел ударника, поршень-боек которого совершает возвратно-поступательное движение под действием сил давления на его рабочие поверхности. Уравнение движения бойка имеет вид:

(1)

где маса поршня-бойка; х – координата положения поршня-бойка положение; - давления жидкости в соответствующих рабочих камерах; - площади рабочих поверхностей поршня-бойка в соответствующих камерах; - сила трения, создаваемая резиновыми уплотнениями (кольцами) поршня-бойка, рассчитывается по формуле:

. (2)

В соответствии с классической теорией удара скорость после соударения с инструментом определяется формулой

при ,

где - коэффициент восстановления скорости, который может находиться в пределах [3] 0,1 …0,3.

Подвижным элементом узла распределителя является поршень-клапан, уравнение движения которого имеет вид:

(3)

Рис. 1. Расчетная гидравлическая схема ударного механизма

здесь - масса поршня-клапана; z – координата поршня; - давления жидкости в соответствующих рабочих камерах; - площади рабочих поверхностей; – сила трения, которая рассчитывается по формуле:

При достижении поршнем-клапаном одного из крайних положений (, скорость его гасится до нуля.

Давление в камере D определяется давлением ГПА и в соответствии с допущением описывается уравнением адиабаты:

, (5)

начальные давление и объем закачки газа в ГПА; - текущие значения давления и объема ГПА в рабочем процессе; k=1.4 -коэффициент адиабаты. Текущий объем определяется объемом рабочей жидкости, поступающим и отдаваемым ГПА:

(6)

- расход рабочей жидкости, поступающий в ГПА.

Давления в рабочих камерах рассчитываются по формулам:

, – давления в соответствующих рабочих камерах. Расходы определяются скоростью движения поршня-бойка: . – гидравлические сопротивления каналов, соединяющих соответствующие камеры. - переменное гидравлическое сопротивление между седлом и клапаном, рассчитываемое по формуле [ 4]:

где - диаметр клапана, - расстояние от клапана до седла (величина открытия клапана), - переменный коэффициент расхода, зависящий от положения клапана, может быть представлен в соответствии с данными [5] таблично заданной функцией (см. табл.1), позволяющей применить линейную интерполяцию между соседними координатами.

Табл.1.

Давления в камерах клапана-распределителя:

Здесь - гидравлическое сопротивление канала ВЕ, – переменное гидравлическое сопротивление между головкой клапана и седлом со стороны сбросной магистрали, рассчитываемое по формуле , – сосредоточенное сопротивление сбросной магистрали. – расход, определяемый скоростью перемещения клапана распределителя, - расход, поступающий в сбросную магистраль. Давление в камере С можно выразить и как

.

Связь расходов в рассматриваемой системе (см.рис.1) выражается следующими уравнениями баланса:

- расход жидкости, поступающий в молоток равен расходу, потребляемому молотком ;

- баланс расходов относительно можно выразить как .

Здесь - расход рабочей жидкости, подаваемый к гидроударному механизму из напорной магистрали (задается исходя их характеристики питающего насоса).

Таким образом, для определения состояния системы необходимо решение дифференциальных уравнений движения поршня-бойка (1) и клапана (2) с учетом функциональных коэффициентов, задаваемых алгебраическими и интегральными зависимостями (2,4,5,6). Полученная система уравнений не может быть решена аналитически из-за существенной нелинейности граничных условий, поэтому решение осуществлялось численно путем имитационного моделирования рабочего процесса. С целью проверки адекватности разработанной математической модели было проведено сравнение осциллограмм рабочего процесса, полученных опытным путем на натурном образце гидромолотка и в результате моделирования на компьютере. На рис.2 показаны графики зависимости скорости движения бойка для натурного и машинного экспериментов. Сравнение предударной скорости бойка показало, максимальное отклонение составило 15.6 % , а среднеквадратическое отклонение

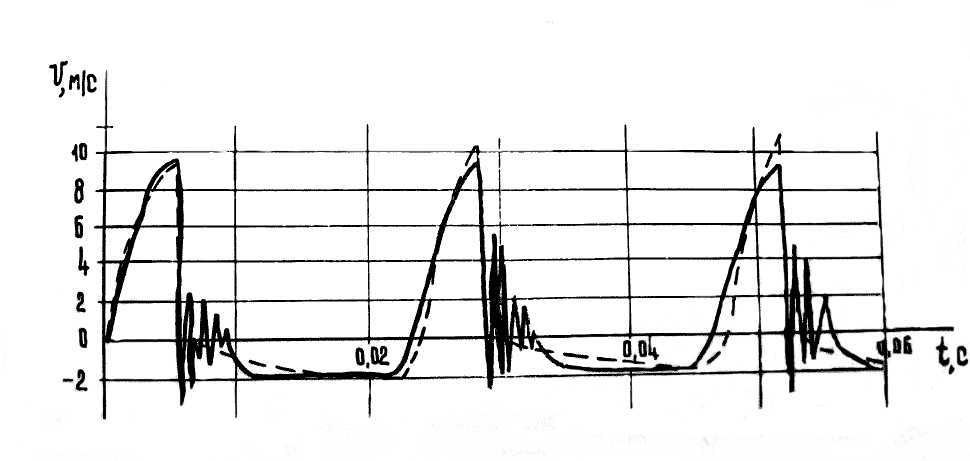
Рис.2. К проверке адекватности математической модели

не превышает 4%. Это свидетельствует об адекватности имитационной модели натурной с точностью, достаточной для прикладных исследований.

Направление дальнейших исследований. Полученные результаты дают возможность проведения исследований как ручных, так и более мощных механизмов, и использованием построенной математической модели, реализованной в виде имитационного алгоритма, адекватность которой доказана на основании сравнения результатов моделирования и натурного эксперимента. Разработанная имитационная модель может быть использована для оптимизации разрабатываемых конструкций гидравлических ударных механизмов.

Список источников:

1. Соколинский Б.В. Машины ударного разрушения (Основы комплексного проектирования).-М.: Машиностроение, 1982.-184с.

2. Тимошенко Г.М., Устименко Т.А., Мартыненко В.Ф.Гидравлический отбойный молоток ГМ-9// Уголь Украины,- 1988.-№12.-с.24-26.

3. Селивра С.А. Разработка гидравлических устройств ударного действия для разрушения горных пород. Дисс. … канд. техн. наук:05.05.06.-Донецк,1986.-194 с.

4. Гидравлика, гидромашины и гидроприводы: Учебник для машиностроительных вузов/Т.М. Башта, С.С.Руднев, Б.Б. Некрасов и др. – М.: Машиностроение, 1982.-423с.

5. Караев М.А. Гидравлика буровых насосов. – М.: Недра, 1983.-208 с.

К библиотеке